- 1【Python绘图入门之plt.plot函数详解】
- 2基于SpringBoot的“考研资讯平台”的设计与实现(源码+数据库+文档+PPT)_基于springboot的考研学习交流系统设计与实现
- 3linux 命令行下批量解压当前目录下的所有zip文件到指定目录_linux批量解压zip文件
- 42025南京理工大学计算机考研信息汇总
- 5最新百度 阿里 华为 腾讯 谷歌面试笔试题及解析_小红拿到了一个数组,她准备选择一个子序列,使得该子序列的中位数尽可能大。奇数长
- 6权限框架之Shiro详解
- 7SqlMap之mysql数据库注入_sqlmap mysql注入
- 8探秘 Flask-Admin:优雅地构建你的 Python 后台管理界面
- 9map()函数介绍:_.map()函数
- 10【Eclipse】安装与卸载教程_如何卸载eclipse重新安装
One PUNCH Man——激活函数和梯度消失/爆炸_csdnone punch man
赞
踩
首先推荐一个写公式的网站:https://private.codecogs.com/latex/eqneditor.php
什么是激活函数
如下图,在神经元中,输入的 inputs 通过加权,求和后,还被作用了一个函数,这个函数就是激活函数 Activation Function。

如果不用激励函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合。
如果使用的话,激活函数给神经元引入了非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以应用到众多的非线性模型中。
激活函数介绍
- sigmoid函数: f ( x ) = 1 1 + e − x f(x)=\frac{1}{1+e^{-x}} f(x)=1+e−x1
sigmoid函数定义域是R,其值域为「0,1」,所以可以用来二分类(1,0),在特征相差比较复杂或是相差不是特别大时效果比较好。
sigmoid函数的导数:
f
′
(
x
)
=
f
(
x
)
∗
(
1
−
f
(
x
)
)
f'(x)=f(x)*(1-f(x))
f′(x)=f(x)∗(1−f(x)),导函数值域为(0,0.25]

sigmoid缺点:
- 激活函数计算量大,反向传播求误差梯度时,求导涉及除法
- 反向传播时,很容易就会出现梯度消失的情况,从而无法完成深层网络的训练
- Sigmoids函数饱和且kill掉梯度
- Sigmoids函数收敛缓慢
sigmoid 原函数及导数图形如下:

由图可知,导数从 0 开始很快就又趋近于 0 了,易造成“梯度消失”现象
- Tanh函数: t a n h ( x ) = e x − e − x e x + e − x tanh(x)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} tanh(x)=ex+e−xex−e−x
Tanh函数也可以表示为:
t
a
n
h
(
x
)
=
2
s
i
g
m
o
i
d
(
2
x
)
−
1
tanh(x)=2sigmoid(2x)-1
tanh(x)=2sigmoid(2x)−1,其定义域为R,值域为(-1,1)
其导函数为:
(
t
a
n
h
(
x
)
)
′
=
s
e
c
h
2
(
x
)
=
1
−
t
a
n
h
2
(
x
)
(tanh(x))'=sech^2(x)=1-tanh^2(x)
(tanh(x))′=sech2(x)=1−tanh2(x),导函数值域为(0,1]

观察sigmoid和tanh的函数曲线,sigmoid在输入处于[-1,1]之间时,函数值变化敏感(导函数最大),一旦接近或者超出区间就失去敏感性,处于饱和状态,影响神经网络预测的精度值。tanh的输出和输入能够保持非线性单调上升和下降关系,符合BP网络的梯度求解,容错性好,有界,渐进于0、1,符合人脑神经饱和的规律,但比sigmoid函数延迟了饱和期。
tanh在特征相差明显时的效果会很好,在循环过程中会不断扩大特征效果。
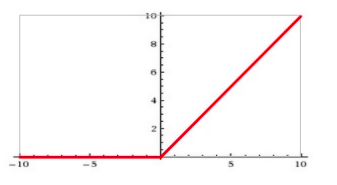
- ReLU函数: ϕ ( x ) = m a x ( 0 , x ) \phi (x)=max(0,x) ϕ(x)=max(0,x)
RELU特点:
- 输入信号 <0 时,输出都是0,>0 的情况下,输出等于输入
ReLU 的优点: - Krizhevsky et al. 发现使用 ReLU 得到的 SGD 的收敛速度会比 sigmoid/tanh 快很多
ReLU 的缺点: - 训练的时候很”脆弱”,很容易就”die”了
例如,一个非常大的梯度流过一个 ReLU 神经元,更新过参数之后,这个神经元再也不会对任何数据有激活现象了,那么这个神经元的梯度就永远都会是 0.
如果 learning rate 很大,那么很有可能网络中的 40% 的神经元都”dead”了。
其导数为:
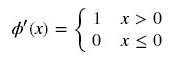
- softmax函数
公式如下:
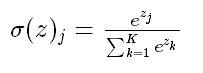
举个例子来看公式的意思:

就是如果某一个 zj 大过其他 z, 那这个映射的分量就逼近于 1,其他就逼近于 0,主要应用就是多分类。
为什么要取指数,第一个原因是要模拟 max 的行为,所以要让大的更大。第二个原因是需要一个可导的函数。
由于初学,现在有个概念就好,点到为止,下一节介绍由sigmoid函数为基础的LR模型算法。
梯度消失/爆炸
这部分是补充内容。在学习了神经网络后会有更好的理解。https://blog.csdn.net/No_Game_No_Life_/article/details/89710077
一般来说就是,由于求导后的连乘导致的梯度消失或者爆炸发生。详见下面的链接:
https://blog.csdn.net/qq_17130909/article/details/80582226


