惯性导航之Runge-Kunta法更新四元数（六）_陀螺仪四元数更新方程

作者：IT小白 | 2024-06-08 08:26:50

踩

陀螺仪四元数更新方程

从陀螺仪得到x、y、z三个角速度后就需要通过积分来得到角度，事实上，经过简单的积分是得不到正确的角度的，更得不到欧拉角，在这里说一下通过的Runge-Kunta更新四元数，从而对角速度积分得到角度的过程。

四元数能到快速的发展，得益于飞行器控制与导航的发展，要求更合理的描述刚体空间的运动，以便于计算机的计算。

在采用方向余弦描述飞行器运动时，要积分矩阵微分方程：
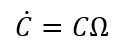
这里写图片描述
C为载体坐标到世界坐标系的方向余弦矩阵，Ω为载体坐标系相对于世界坐标系旋转角速度ω的反对称矩阵。进行计算时将包含9个一阶微分方程，计算量很大。

在使用四元数进行求解时，需要求解四元数方程：
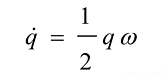
这里写图片描述
其中，q为描述载体坐标系转动的四元数，ω为载体坐标系相对世界坐标系转动的角速度，同样的可以表示为四元数：

ω = 0 + ω_{x} \cdot i + ω_{y} \cdot j + ω_{z} \cdot k

$ω= 0+ω_x·i+ω_y·j+ω_z·k$

按四元数乘积展开：

$q_{0} = \frac{1}{2} (- q_{1} \cdot ω_{x} - q_{2} \cdot ω_{y} - q_{3} \cdot ω_{z})$ $q_0 = \frac{1}{2}(-q_1·ω_x - q_2·ω_y - q_3·ω_z)$
$q_{1} = \frac{1}{2} (q_{0} \cdot ω_{x} + q_{2} \cdot ω_{z} - q_{3} \cdot ω_{y})$ $q_1 = \frac{1}{2}( q_0·ω_x + q_2·ω_z - q_3·ω_y)$
$q_{2} = \frac{1}{2} (q_{0} \cdot ω_{y} - q_{1} \cdot ω_{z} + q_{3} \cdot ω_{x})$ $q_2 = \frac{1}{2}( q_0·ω_y - q_1·ω_z + q_3·ω_x)$
$q_{3} = \frac{1}{2} (q_{0} \cdot ω_{z} + q_{1} \cdot ω_{y} - q_{2} \cdot ω_{x})$ $q_3 = \frac{1}{2}( q_0·ω_z + q_1·ω_y - q_2·ω_x)$
只需要解四个一阶微分方程。

了解过微分方程的应该知道，只有一小部分的微分方程是可以求出通解的，剩下的大部分都需要其他的一些方法来了解性质或者求数值解等等。

Runge-Kunta法就是一种常微分方程的数值解法，可以求得常微分方程的近似数值解，可以参考《数值分析》之类的数学书籍深入了解。

这里先给出四阶标准R-K公式：

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/IT小白/article/detail/689126