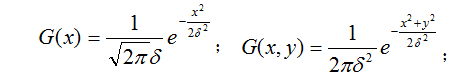几种典型的图像去噪算法总结_图像降噪算法

（一）高斯低通滤波去噪

        高斯低通滤波器（Gaussian Low Pass Filter）是一类传递函数为高斯函数的线性平滑滤波器。又由于高斯函数是正态分布的密度函数。因此高斯低通滤波器对于去除服从正态分布（Normal distribution）的噪声非常有效。一维高斯函数和二维高斯函数 (高斯低通滤波器的传递函数) 的表达形式分别如下：

        公式中，为标准差，由于图像通常是二维信号，因此图像去噪通常使用二维高斯函数作为传递函数，而高斯函数具有可分离的特性，因此可以先对行进行高斯滤波，再对列进行高斯滤波，这样二维高斯函数就可以降为一维高斯滤波。下图1分别模拟了标准差为10和标准差为50的高斯函数。

图1：不同标准差时的高斯曲线

从上图可以看出，高斯函数的标准差越大，高斯曲线越平滑。去噪能力越强，图像越模糊。

        下图2用均值为0方差分别为0.1,0.5,1.0的高斯噪声对原图像进行污染的结果。

图2

        高斯滤波的实现方式有时域方式和频域方式两种，一种是时域高斯低通滤波，一种是频域高斯低通滤波。下面首先看看时域高斯低通滤波的结果。时域高斯低通滤波的实质是定义一个奇数大小的模板（3 X 3 ；5 X 5 ；7 X 7 ……），然后让该模板遍历整副图像，模板中的加权平均值就是模板中心的值。时域高斯低通滤波的结果如下图所示：

图3：不同的标准差和领域大小时的去噪后的图像

        从上图可以看出，当领域窗口固定时，标准差越大，去除高斯噪声能力越强，图像越模糊，当标准差为2以上时，去噪能力几乎不再增加，只有当增加领域的大小时，去噪能力才会进一步增强。下面我们可以看一下，标准差分别为10和30的高斯曲线来进一步说明在邻域窗口大小一致的情况下，标准差越大，高斯曲线越宽，那么去高频噪声的能力就越强。但是他不是无限增强的，最终会趋于一个稳定值，只有当继续增大邻域窗口时，去噪能力才会进一步增强。

图4：不同标准差时的高斯曲线

        上述时域高斯低通滤波的matlab源代码如下：

%时域高斯低通去噪
x = imread('NoiseImage.jpg');
subplot(231),imshow(x);title('高斯噪声为0.1的原图')
y1 = fspecial('gaussian',5,0.1);
z1 = imfilter(x,y1,'symmetric');
subplot(232),imshow(z1);title('领域窗口大小为5X5,标准差为0.1');
y2 = fspecial('gaussian',5,2);
z2 = imfilter(x,y2,'symmetric');
subplot(233),imshow(z2);title('领域窗口大小为5X5,标准差为2');
y3 = fspecial('gaussian',5,3);
z3 = imfilter(x,y3,'symmetric');
subplot(234),imshow(z3);title('领域窗口大小为5X5,标准差为3');
y4 = fspecial('gaussian',5,5);
z4 = imfilter(x,y4,'symmetric');
subplot(235),imshow(z4);title('领域窗口大小为5X5,标准差为5');
y4 = fspecial('gaussian',11,5);
z4 = imfilter(x,y4,'symmetric');
subplot(236),imshow(z4);title('领域窗口大小为11X11,标准差为5');

        下面实现频域高斯低通滤波器

       由于时域滤波的本质就是采用原始图像与滤波核（领域窗口）进行卷积的操作，我们知道卷积的运算速度是比较慢的，由傅里叶变换的性质可知，时域卷积可以转化为频域的乘积。因而频域高斯低通滤波应运而生。该部分内容基本源于冈萨雷斯版数字图像处理中第四章的内容，为了避免抄书，这里仅给出与时域滤波有相似结果的频域滤波的matlab源代码。

        频域高斯低通滤波器的传递函数为：；Matlab自带了低通滤波器函数lpfilter；它的源代码如下：

function H = lpfilter(type, M, N, D0, n)
%LPFILTER Computes frequency domain lowpass filters.
%   H = LPFILTER(TYPE, M, N, D0, n) creates the transfer function of
%   a lowpass filter, H, of the specified TYPE and size (M-by-N). To
%   view the filter as an image or mesh plot, it should be centered
%   using H = fftshift(H). 
%
%   Valid values for TYPE, D0, and n are:
%
%   'ideal'    Ideal lowpass filter with cutoff frequency D0. n need
%              not be supplied.  D0 must be positive.
%
%   'btw'      Butterworth lowpass filter of order n, and cutoff
%              D0.  The default value for n is 1.0.  D0 must be
%              positive.
%
%   'gaussian' Gaussian lowpass filter with cutoff (standard
%              deviation) D0.  n need not be supplied.  D0 must be
%              positive. 
[U, V] = dftuv(M, N);


% Compute the distances D(U, V).
D = sqrt(U.^2 + V.^2);


% Begin filter computations.
switch type
case 'ideal'
   H = double(D <= D0);
case 'btw'
   if nargin == 4
      n = 1; 
   end
   H = 1./(1 + (D./D0).^(2*n));
case 'gaussian'
   H = exp(-(D.^2)./(2*(D0^2)));
otherwise
   error('Unknown filter type.')
end

        为了防止傅里叶变换时由于周期性而导致的相邻周期之间的干扰，需要对输入图像进行0填充，对应于时域滤波中的imfilter函数中的“symmetric”选项。频域中采用paddedsize函数来实现。频域高斯低通滤波的matlab代码如下：

f = imread('NoiseImage.jpg');
subplot(221)
imshow(f);title('原图')
f_r = f(:,:,1);
f_g = f(:,:,2);
f_b = f(:,:,3);
[M,N] = size(f_r);
sig1 = 50;                                   %%截止频率
PQ = paddedsize(size(f_r));                 %%确定输入图像补0后的边界大小       
Fp_r = fft2(f_r,PQ(1),PQ(2));               %% R通道傅里叶变换
Fp_g = fft2(f_g,PQ(1),PQ(2));              
Fp_b = fft2(f_b,PQ(1),PQ(2));
Hp1 = lpfilter('gaussian',PQ(1),PQ(2),2*sig1); %%生成高斯低通滤波，
Gp_r1 = Hp1.*Fp_r;                             %% R通道高斯低通滤波
Gp_g1 = Hp1.*Fp_g;
Gp_b1 = Hp1.*Fp_b;
gp_r1 = real(ifft2(Gp_r1));                    %% 取得R通道的傅里叶反变换；
gp_g1 = real(ifft2(Gp_g1));
gp_b1 = real(ifft2(Gp_b1));
gpc_r1 = gp_r1(1:size(f,1),1:size(f,2));
gpc_g1 = gp_g1(1:size(f,1),1:size(f,2));
gpc_b1 = gp_b1(1:size(f,1),1:size(f,2));
gpc1 = cat(3,gpc_r1,gpc_g1,gpc_b1);
gpc1 = uint8(gpc1);
subplot(222),imshow(gpc1);title('截止频率为50的低通滤波')
%%下面计算截止频率为30的频域高斯低通滤波
sig2 = 30;
Hp2 = lpfilter('gaussian',PQ(1),PQ(2),2*sig2); %%生成高斯低通滤波，
Gp_r2 = Hp2.*Fp_r;                             %% R通道高斯低通滤波
Gp_g2 = Hp2.*Fp_g;
Gp_b2 = Hp2.*Fp_b;
gp_r2 = real(ifft2(Gp_r2));                    %% 取得R通道的傅里叶反变换；
gp_g2 = real(ifft2(Gp_g2));
gp_b2 = real(ifft2(Gp_b2));
gpc_r2 = gp_r2(1:size(f,1),1:size(f,2));
gpc_g2 = gp_g2(1:size(f,1),1:size(f,2));
gpc_b2 = gp_b2(1:size(f,1),1:size(f,2));
gpc2 = cat(3,gpc_r2,gpc_g2,gpc_b2);
gpc2 = uint8(gpc2);
subplot(223),imshow(gpc2);title('截止频率为30的低通滤波')
%%下面计算截止频率为10的频域高斯低通滤波
sig2 = 10;
Hp3 = lpfilter('gaussian',PQ(1),PQ(2),2*sig2); %%生成高斯低通滤波，
Gp_r3 = Hp3.*Fp_r;                             %% R通道高斯低通滤波
Gp_g3 = Hp3.*Fp_g;
Gp_b3 = Hp3.*Fp_b;
gp_r3 = real(ifft2(Gp_r3));                    %% 取得R通道的傅里叶反变换；
gp_g3 = real(ifft2(Gp_g3));
gp_b3 = real(ifft2(Gp_b3));
gpc_r3 = gp_r3(1:size(f,1),1:size(f,2));
gpc_g3 = gp_g3(1:size(f,1),1:size(f,2));
gpc_b3 = gp_b3(1:size(f,1),1:size(f,2));
gpc3 = cat(3,gpc_r3,gpc_g3,gpc_b3);
gpc3 = uint8(gpc3);
subplot(224),imshow(gpc3);title('截止频率为10的低通滤波')

仿真结果如下：

        高斯低通滤波虽然较为简单，个人觉得将它说的非常明白，还是有些困难，这与自己的表达能力差有很大的关系，以后要养成些博客的习惯，希望能够尽早提高。我还是习惯用时域滤波的方法，频域滤波可以将时域的卷积运算转化为频域乘积运算，然而时域转化为频域过程中的傅里叶计算同样耗费时间。时域运算是领域操作，而频域计算式整体操作，关于时域和频域孰优孰劣还有待进一步考究。

       高斯低通滤波应该是最基本的去噪手段，后面将进一步阐述双边滤波去噪、非局部均值去噪，以及核回归用于图像去噪。

-------------------------------------------任何一个理论，无论它是简单还是复杂，都应该将它剖析的非常清楚，这样才有可能将复杂的问题简单化，首先要将自己说服，才有可能让别人信服----------------------------------------------