C++启发式搜索算法（A*），给你一点阳光，你一定要灿烂哟！

公众号：编程驿站

1. 前言

给小孩子出一道数学题，在他不知所措，没有头绪时，你给他点提示。也许这点提示可以让他灵光一现，找到一点光亮，少一些脑回路，快速找到答案。这便是启发的作用。

启发式搜索(Heuristically Search)又称为有信息搜索(Informed Search)，是利用问题拥有的启发信息来引导搜索，达到减少搜索范围、降低问题复杂度的目的，这种利用启发信息的搜索过程称为启发式搜索。

启发式搜索的目的是减少搜索的不必要性，搜索的本质是无目地性的。对于原始搜索算法，搜索之初，并不知道搜索的目标具体在何方，所以，需要朝所有方向搜索，一旦找到便结束搜索。显然，必然会有些搜索是吃亏不讨好的。

**Tips：**本文的原始搜索，指深度和广度搜索。

如下图的迷宫问题中，搜索目标在迷宫的右下角，如果原始搜索算法的设定是朝四个方向出发，则可以在编码时可以给搜索指引方向，也就是提供启发式引导，减少不必要的搜索范围。如下图中搜索时，可以只向南和东向搜索。

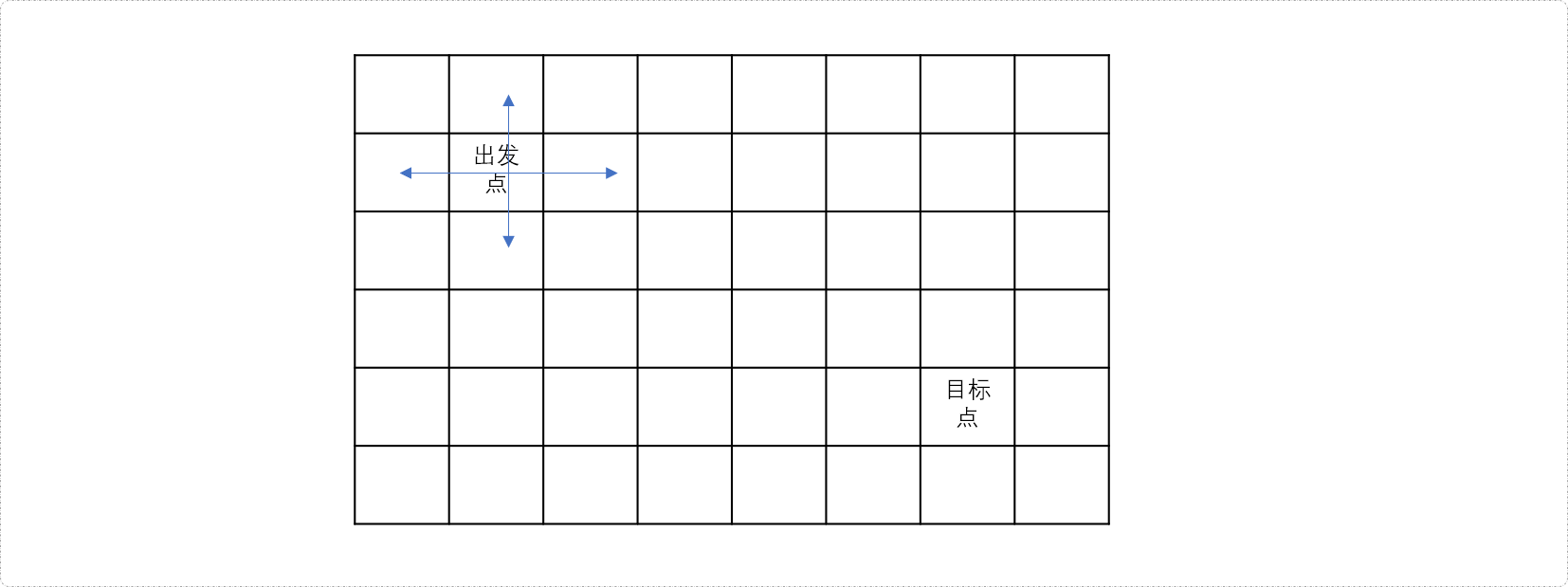
所以在搜索时，提供适当的指引，可以修正搜索一直朝最正确的方向进行，从而减少不必要的搜索。

那么如何设计指引方案，即如何设计启发式算法。

2. 启发式搜索

原始搜索算法的本质是多状态的、且盲目的，启发式搜索就是在原始搜索算法基础之上提供一盏指引方向的灯，在多路口时，尽量朝目标路口前进。这盏灯在启发式搜索中称为估价函数。

估价函数

估价函数指的是为当前点到终点之间的所有状态做出一个估计值，代表选择不同状态时的要付出的代价。

如上图的迷宫问题。

• 如果从出发点的上方或左边方向搜索，离目标点越来越远。其估计值大于实际值（出发点到目标点的实际距离）。
• 如果从出发点的下方或右边方向搜索，离目标点会越来越近。其估计值会接近实际值。

如何对一个状态（选择）进行评估呢？

一个状态的当前代价最小，只能说明从初始状态到当前状态的代价最小，不代表总的代价最小，因为余下的路还很长，未来的代价有可能更高。因此评估需要考虑两部分：当前代价和未来代价。

评估函数f(x)=g(x)+h(x)，其中，g(x)表示从初始状态到当前状态x的代价，h(x)表示从当前状态到目标状态的估价，h(x)被称为启发函数。

当前状态的代价是已知的，更多时候在意未来的路有多长，在估价函数的组成中，启发函数更具有指导性作用。

在设计估价函数时，需遵循一个基本原则：估计值必须比实际更优(估计代价<=实际代价)。

如果估计值大于实际值，则在最优解搜索路径上的状态被错误指引，从而导致非最优解搜索路径上的状态不断扩展，直至在目标状态上产生错误的答案。如上述迷宫问题时，如果估计方向朝上，则会离目标越来越远。

如果估计值不大于实际值，这个值总会比最优解更早地被取出，从而得到修正。即使得不到最优解，无非就是算的状态多了，搜索时间长一些。

常用的启发式搜索算法有很多，如：

• A*（A-Star）算法，典型的启发式搜索算法。**是带有评估函数的优先队列式广度优先搜索算法；**是一种静态路网中求解最短路径最有效的直接搜索方法，也是解决许多搜索问题的有效算法。

  A*算法使用优先队列存储当前状态下可选择的所有后续状态，优先队列的优先策略由评估函数决定，即每次从优先队列中选择出估计值最少的状态。

  启发式函数的设计决定了A*算法的性能。

  启发函数h(x)越接近当前状态到目标状态的实际代价h′(x)，A*算法的效率就越高。

  启发函数的估值不能超过实际代价，即h(x)≤h′(x)。

  如果启发式函数的值为0，则变成普通的优先队列广度搜索。

• IDA*、模拟退火算法、蚁群算法、遗传算法等。

  IDA*算法是带有评估函数的迭代加深DFS算法。使用评估函数避免深度搜索无止境地向深处搜索，当到达一个阈值后，停止搜索，立即回溯。

估价函数设计算法

无向图中：

• 如果图形中只允许朝上下左右四个方向移动，则可以使用曼哈顿距离。

  曼哈顿距离公式=|x₁-x₂|+|y₁-y₂|

• 如果图形中允许朝八个方向移动，则可以使用对角距离。

  对角距离公式：

• 如果图形中允许朝任何方向移动，则可以使用欧几里得距离。

  欧几里得距离公式：

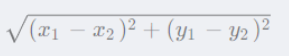
有向图中一般对反向图求终点到源点的最短距离为启发函数。

理论有了，现在开始实战。

2.1 A*算法

例题：第K短路

给定一张 N 个点（编号 1,2…N），M 条边的有向图，求从起点 S 到终点 T 的第 K 短路的长度，路径允许重复经过点或边。

注意： 每条最短路中至少要包含一条边。

输入格式

第一行包含两个整数 N 和 M。

接下来 M 行，每行包含三个整数 A,B 和 L，表示点 A 与点 B 之间存在有向边，且边长为 L。

最后一行包含三个整数 S,T 和 K，分别表示起点 S，终点 T 和第 K 短路。

输出格式

输出占一行，包含一个整数，表示第 K 短路的长度，如果第 K 短路不存在，则输出 −1。

问题分析

回顾迪杰斯特拉算法

典型的单源最短路径问题。算法较多，性能较好的是迪杰斯特拉。但是本题是求第k短路径，是否可以使用此算法求解？

至于是否能否求解，暂且放一放。来回顾一下迪杰斯特拉算法的流程，且放大流程中的细节，看是否能找到一些解决问题的蛛丝马迹。

• 构建如下的图结构。如果s=1、t=6，即求解 1-6之间的最短路径。

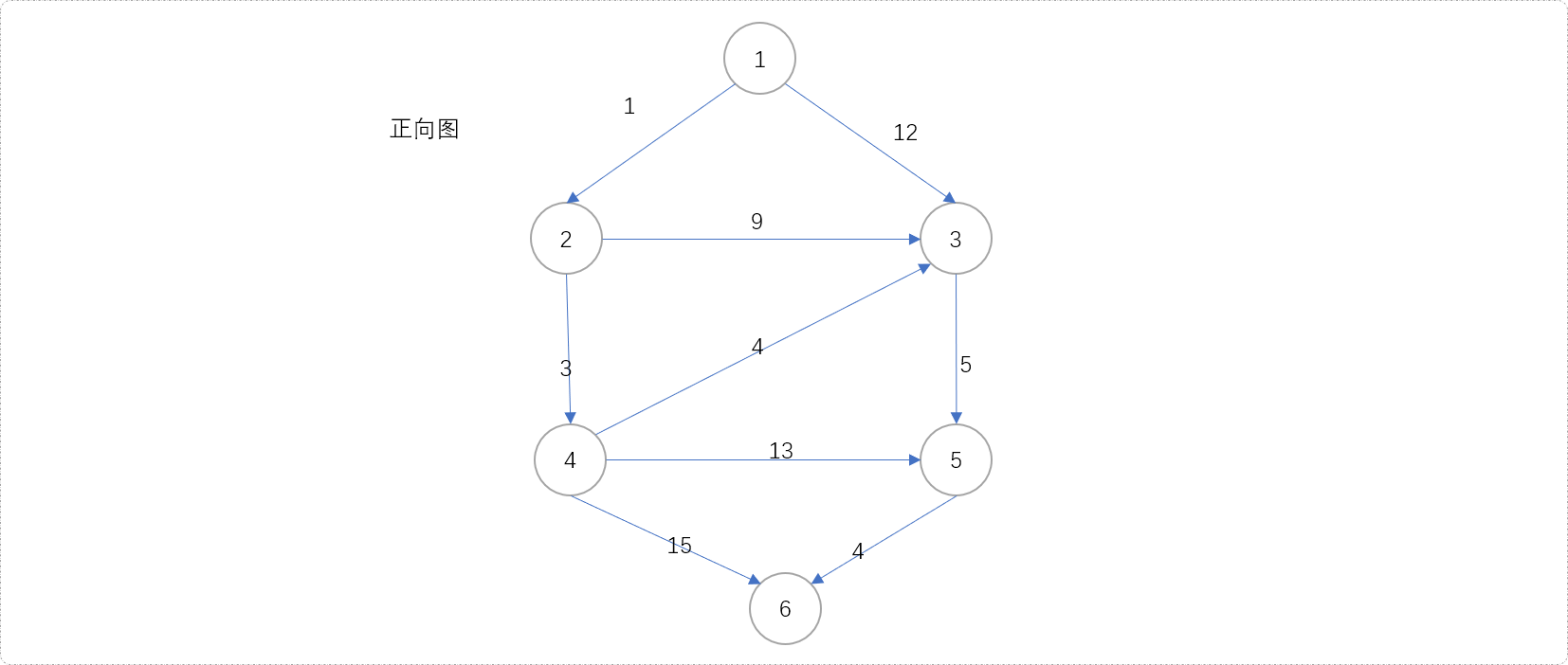
• 我这里直接使用迪杰斯特拉算法，不甚了解此算法的，可以翻阅相关文档。准备一个优先队列，用来存储节点，优先队列的策略以节点到源点的距离为参考；准备一个一张二维数组，用来存储当前节点到源点之间的最短距离。初始dis[1][1]=0。即源点到自身的最短距离为0。

  **Tips：**熟悉迪杰斯特拉算法的可能要问，为什么要准备一张二维数组？不急，在讲解流程中慢慢揭晓。

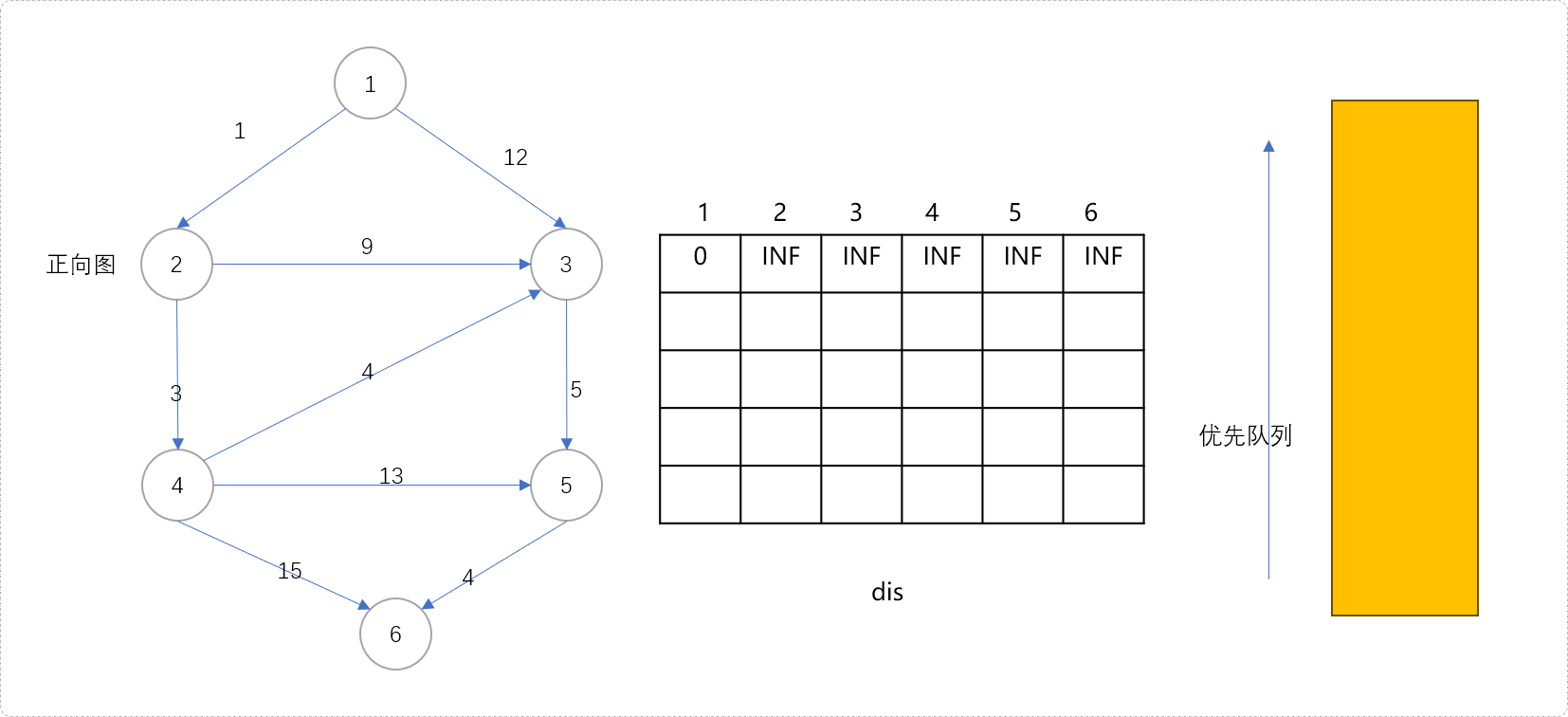
• 初始化队列。把源点1及其最短距离0组合成一个二无信息(1,0)一起入队列。

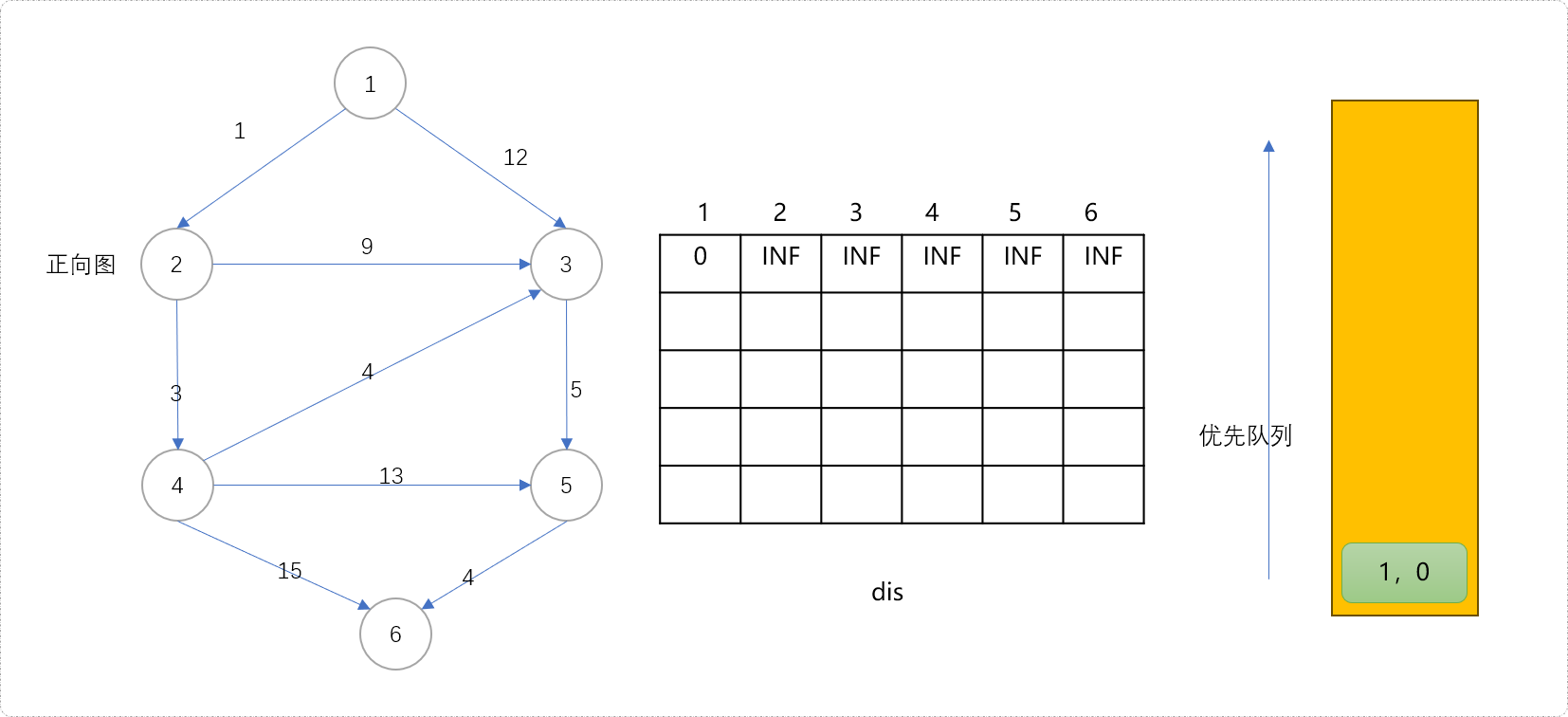
• 扩展队列，从队列中拿出头节点，扩展其子节点。扩展过程中更新子节点到源点的最短距离。节点1可以扩展节点2和3。因节点2和3原来到源点的距离是INF，现在分别被更新为1和12。这对于节点2和3来说，这是第一次更新（最短距离并不能一步到位）。

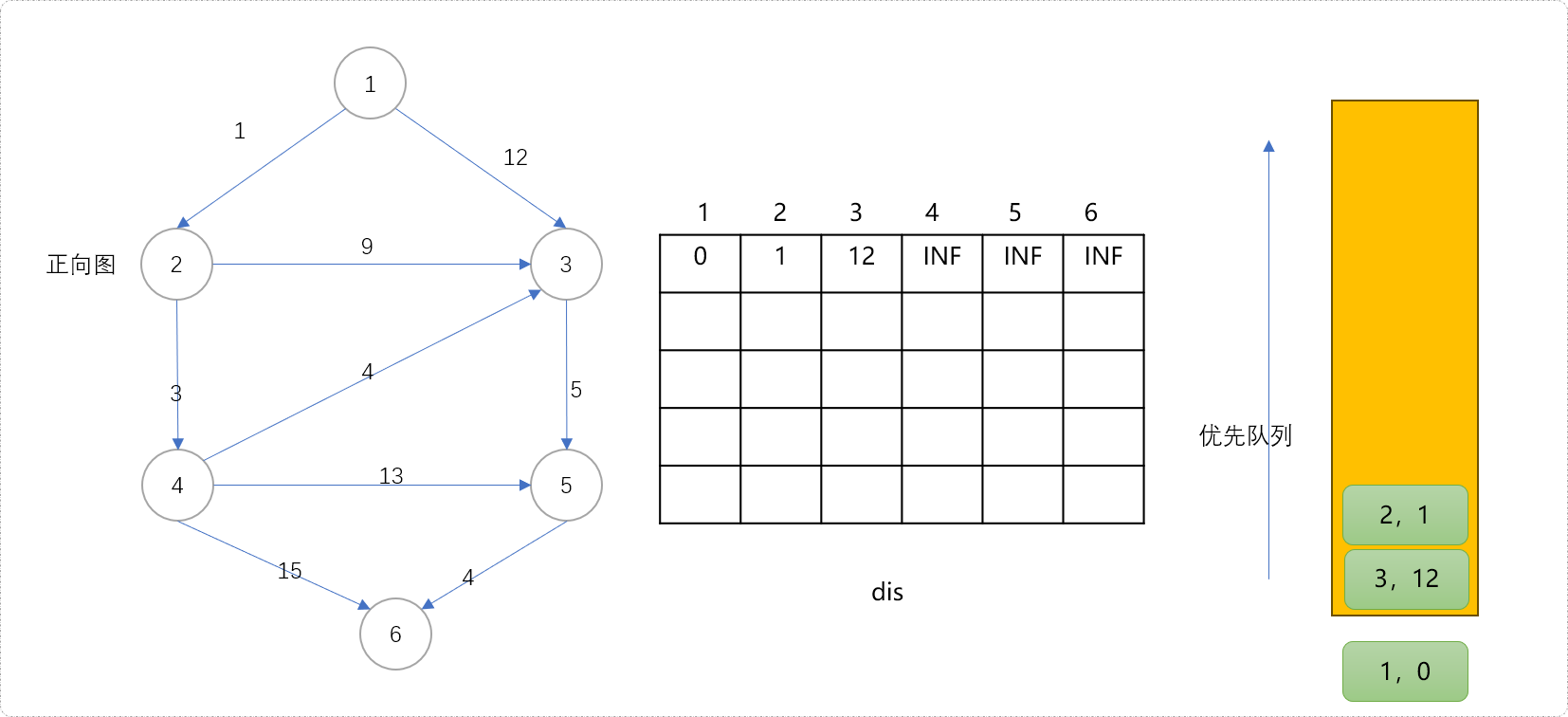
• 根据优先策略。从队列中拿出(2,1)节点。用此节点扩展3和4节点。节点3可以更新为更短距离10，这里节点3的第2次更新。节点4被更新为4，是此节点的第一次更新。如下图所示，相信大家明白了二维数组的作用，存储每一次更新的值。

  思考一下。每一次更新意味着什么？

  对！通过每一次更新，逐渐逼近最短距离，而每一次被更新的值，记录着次最短或说第k短距离。

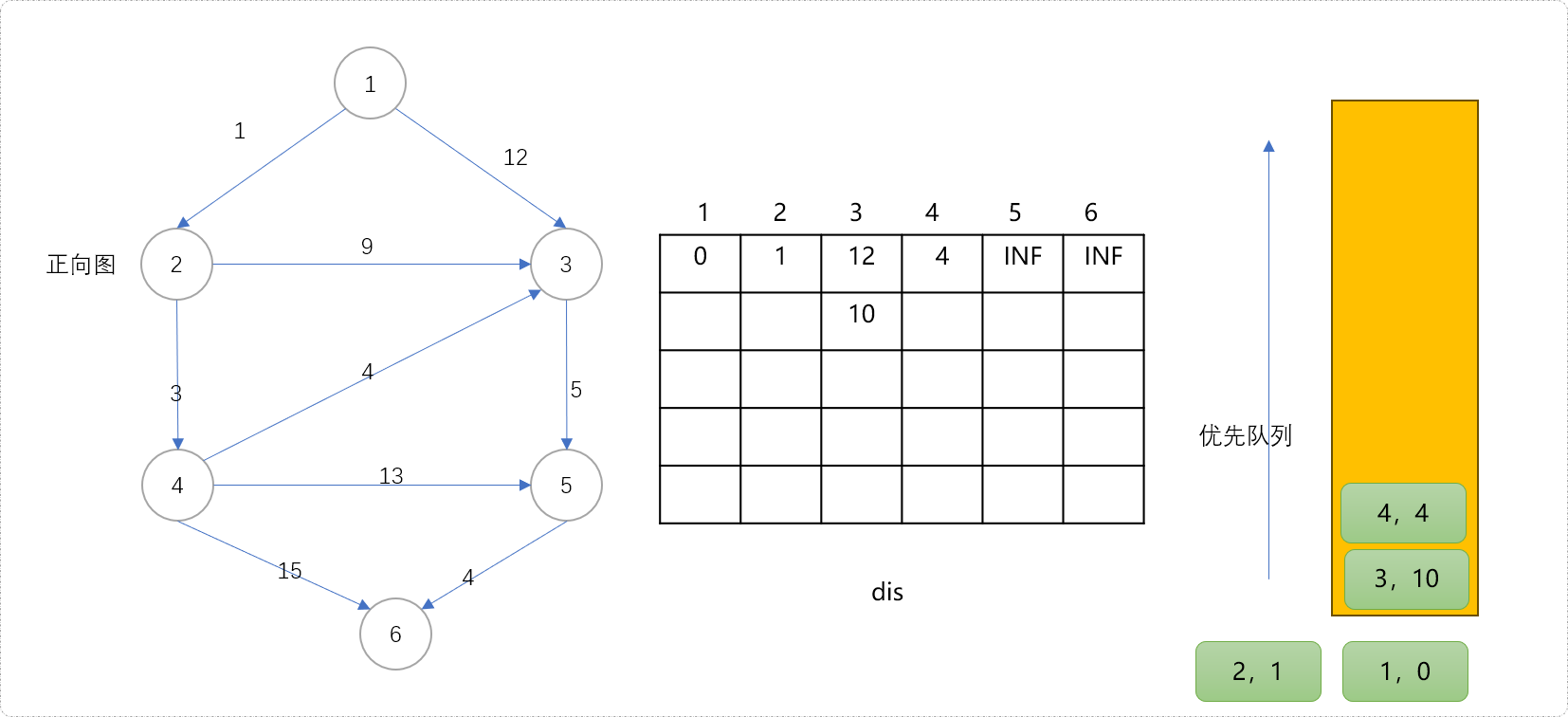
• 从队列中拿出(4,4)节点扩展其子节点。这里得到一个结论，当节点第一次从队列中拿出后，意味着最短距离已经找到。此时节点3更新为8，节点5更新为17，节点6更新为19。

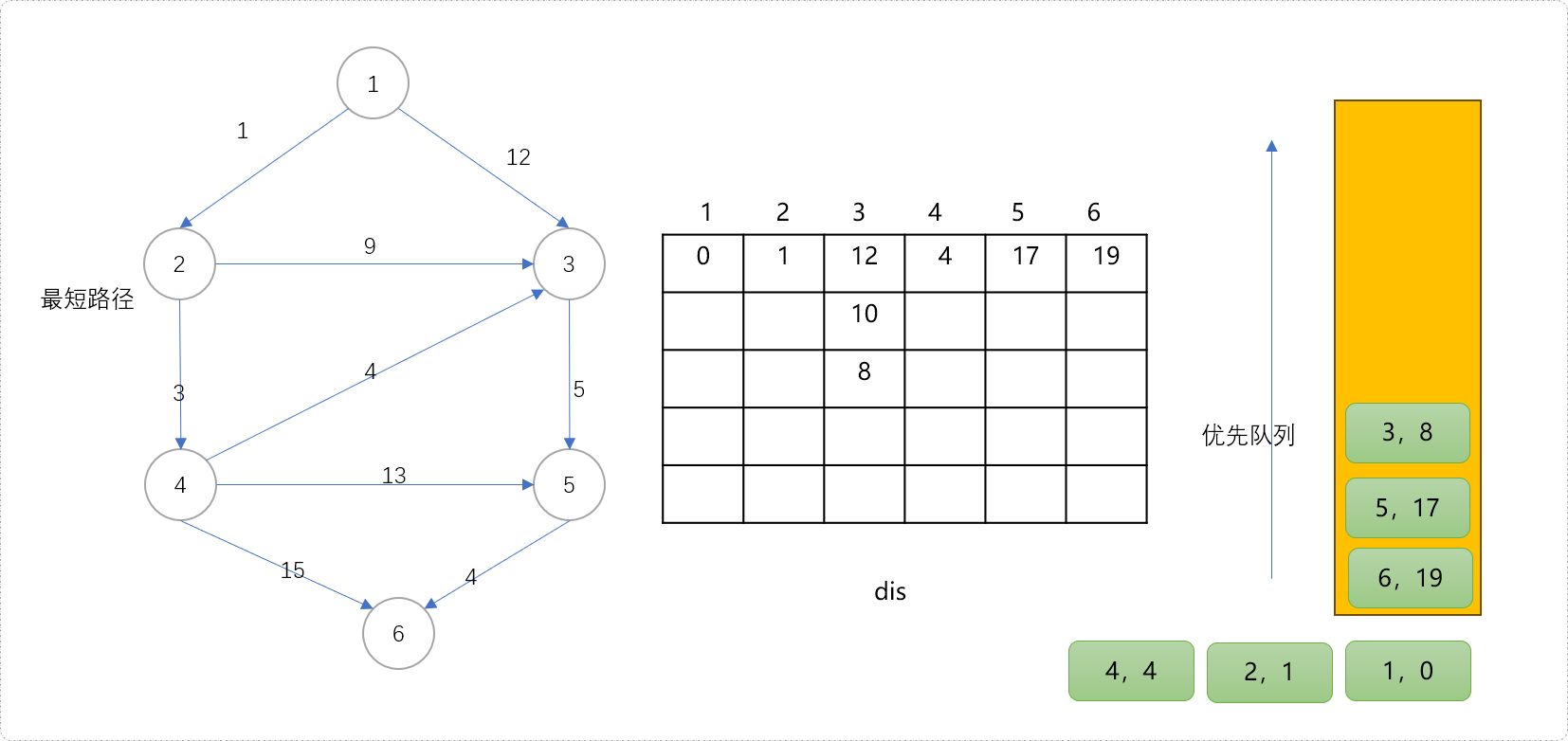
• 从队列中拿出(3,8)节点，意味着节点3到源点1的最短距离为8；次短距离为10，次次短距离为12。是不是惊讶到你了，那么是不是可以说，迪杰斯特拉算法不仅可以求解源点至任意点的最短距离，也可以求解出源点至任意点的第K短路径？

  从现在的情况来看，似乎可以这么认为，而事实是这么说是有瑕疵的，但是至少能得到解决问题的一些线索。

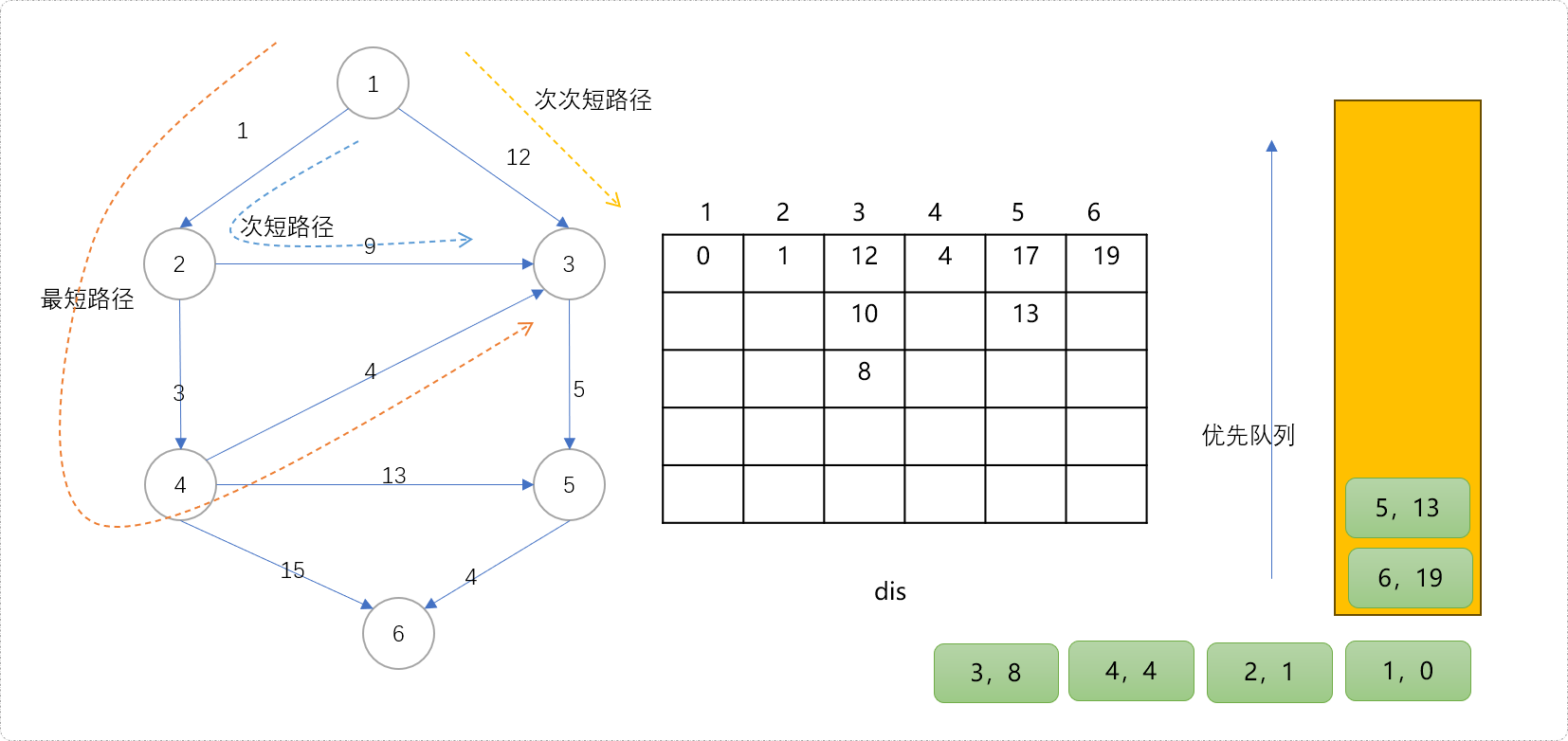
• 下图的二维数组中记录了任意点到源点的所有路径信息。

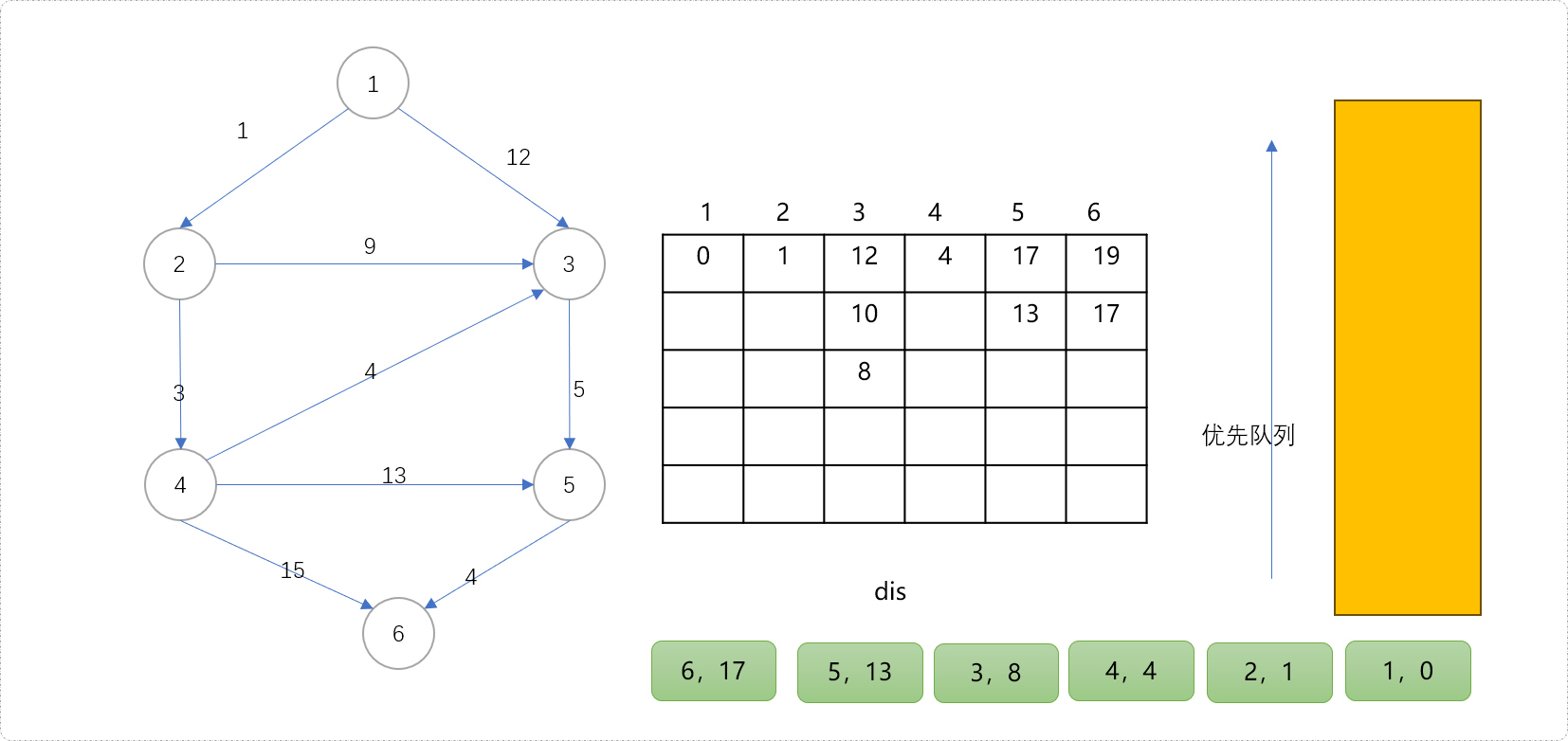
二维表上可以看出，源点至节点3有 3 条路径，直观而言，也只有3条路径。记录上看源点至节点5只有 2 条路径，而实际上不止。因为源点可以经过节点3到节点5，也就是说从源点到节点5至少有3条。同理，源点也可以经过节点4到达节点5，至少有1条。粗算下来，源点到节点5至少应该有4条路径，距离分别为17、15、13、17。

为什么二维数组中的记录节点5的路径只有2条？

原因很简单，迪杰斯特拉算法每次试图做最优更新。如节点5当前值为13，当节点3值为10时，试图更新5号节点是不会成功的。也就得不到值为15的路径。

好了，借次机会详细介绍了迪杰斯特拉算法，仅使用此算法解决第k短路，不是说不行，感觉还是稍有些麻烦。分析到此结束，至于编码就看你的个人兴趣。

A*算法的实现流程

回归正解，计解A*算法。

前文介绍过，A*算法是有带有估计函数的优先队列。估计函数包括两个子函数，一个是当前代价函数g和启发函数h。f(x)=g(x)+h(x)。

g函数计算当前点离源点的最小代价，h函数计算当前点离目标点的预估最小代价。在扩展子节点时，选择两者和最小的子节点扩展，或者说优先队列的优先策略。可以保证搜索过程的方向正确，避免少走不必要的路。

如下图，当选择节点2后，基于搜索的盲目性，即可以向节点3方向，也可以向节点4方向。选择那一条可以减少搜索量？

从2号到3号的g值很容易计算出，1+9=10。也就是从源点到节点3的当前代价是10。

从2号到4号的g值也容易计算出，1+3=4。也就是从源点到节点4的当前代价是4。

是不是理所当然的选择4号节点进行扩展，不能这么早下结论，也许当前的代价很少，但是未来的路很长。当前的最大化利益不能说明未来的利益也是最大化的。

可以用3号和4号节点到目标点(即节点6)的最短路径作为h(x)值。如此算出现在的当前代价和未来的代价之和，方可做为最佳启发值。道理很简单，知道当前代价，也知道未来代码，两者之和，一定是到达目标点的最小代价。

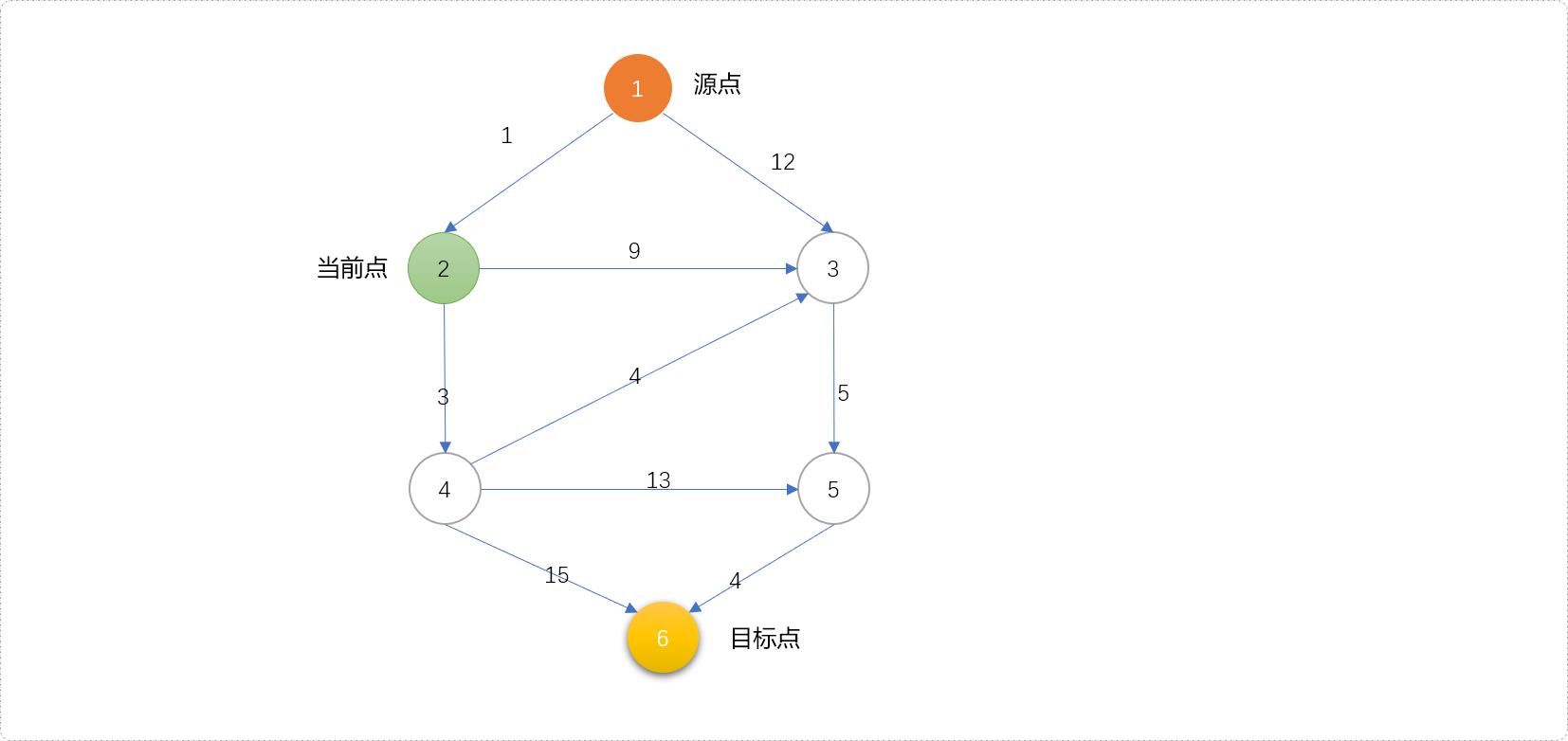
如果能计算出图中的节点到目标点的最短距离，便能得到任一点到目标点的h(x)值。这个实现简单，把原图进行反向，以目标点为源点，走一次迪杰斯特拉算法，便能计算出任意点到目标点的最短距离，用此值作为任意点到目标点的h(x)值。

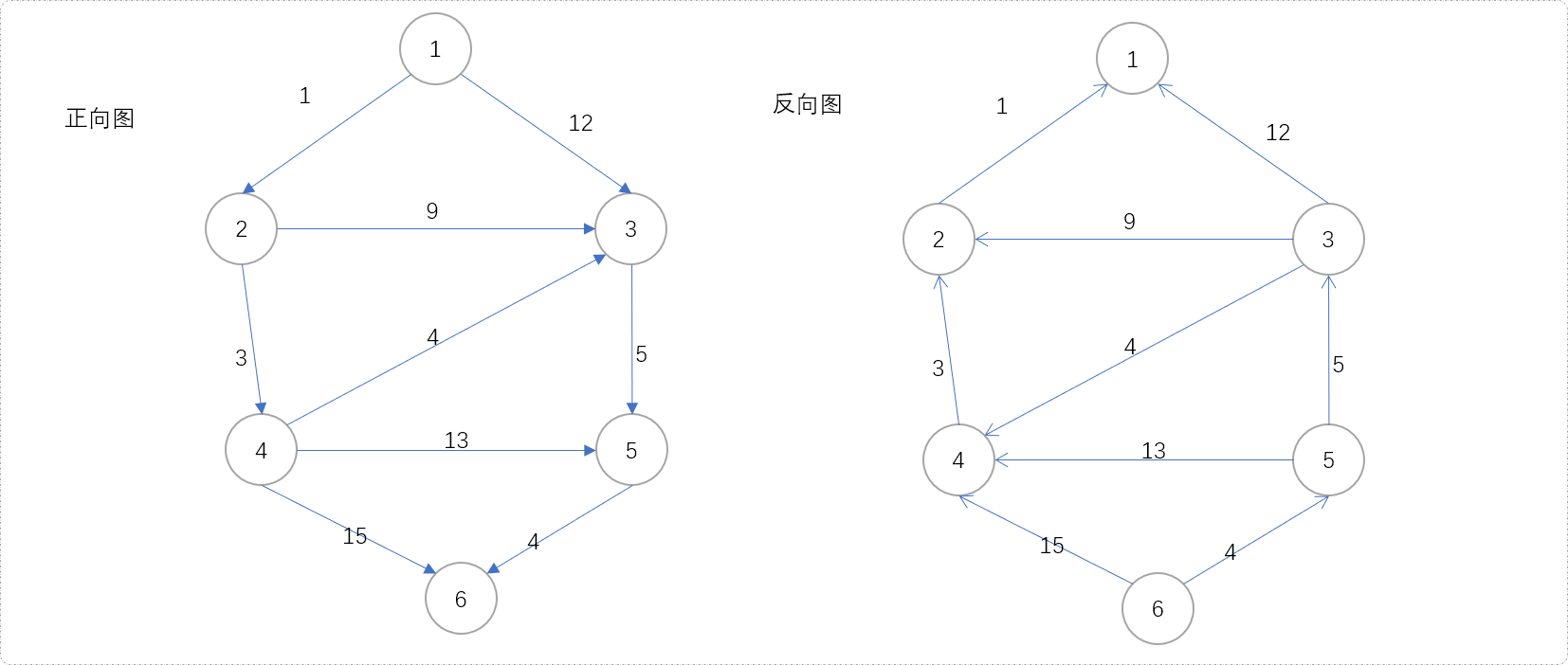
现在，让我们得到反向图中各节点到目标点之间的最短距离。

#include <bits/stdc++.h>
#define MAX 300000 + 50
#define INF 0x3f3f3f3f
using namespace std;

/*
*顶点类型
*/
struct Ver {
	//编号
	int vid;
	//离终点的最短距离
	int toDis=INF;
	//离源点的最短距离
	int fromDis=INF;
	//正向图头指针
	int head=0;
	//反向图头指针
	int rhead=0;

	const bool operator<(const Ver & ver) const {
		return this->toDis>ver.toDis;
	}

} vers[MAX];
//顶点和边数
int n,m;
//边类型
struct Edge {
	//邻接点
	int to;
	//下一个边
	int nex;
	//权重值
	int val;
}  edges[MAX];

//边索引
int tot=0;

//添加边
void addEdge(int type,int f, int t, int w) {
	edges[++tot].to = t;
	edges[tot].val = w;
	if(type==0) {
        //正向边
		edges[tot].nex = vers[f].head;
		vers[f].head= tot;
	} else {
        //反向边
		edges[tot].nex = vers[f].rhead;
		vers[f].rhead= tot;
	}
}

//构建正向图和反向图
void buildGraph() {
	for( int i=1; i<=n; i++ )vers[i].vid=i;
	int f,t,w;
	for(int i = 1; i <= m; ++i) {
		cin >> f >> t >> w;
		addEdge(0,f,t,w);
		addEdge(1,t,f,w);
	}
}
/*
*
*对原图的反图求各节点到目标节点的最短距离
*/
void dijkstra(int s) {
	//优先队列
	priority_queue<Ver>  priQue;
	vers[s].toDis=0;
	//初如化队列
	priQue.push( vers[s] );
	while( !priQue.empty()  ) {
		//取头顶点
		Ver u=priQue.top();
		//删除头顶点
		priQue.pop();
		//扩展子节点
		for( int i=u.rhead; i!=0; i=edges[i].nex ) {
			Ver v=vers[  edges[i].to ];
			if( v.toDis> edges[i].val+u.toDis  ) {
				//更新
				v.toDis= edges[i].val+u.toDis;
				vers[ edges[i].to ]=v;
				priQue.push(v);
			}
		}
	}
}
void show() {
	for(int i=1; i<=n; i++) {
		cout<<vers[i].vid<<"\t"<<vers[i].toDis<<endl;
	}
}

int main() {
	cin>>n>>m;
	buildGraph();
	dijkstra(6);
	show();
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105

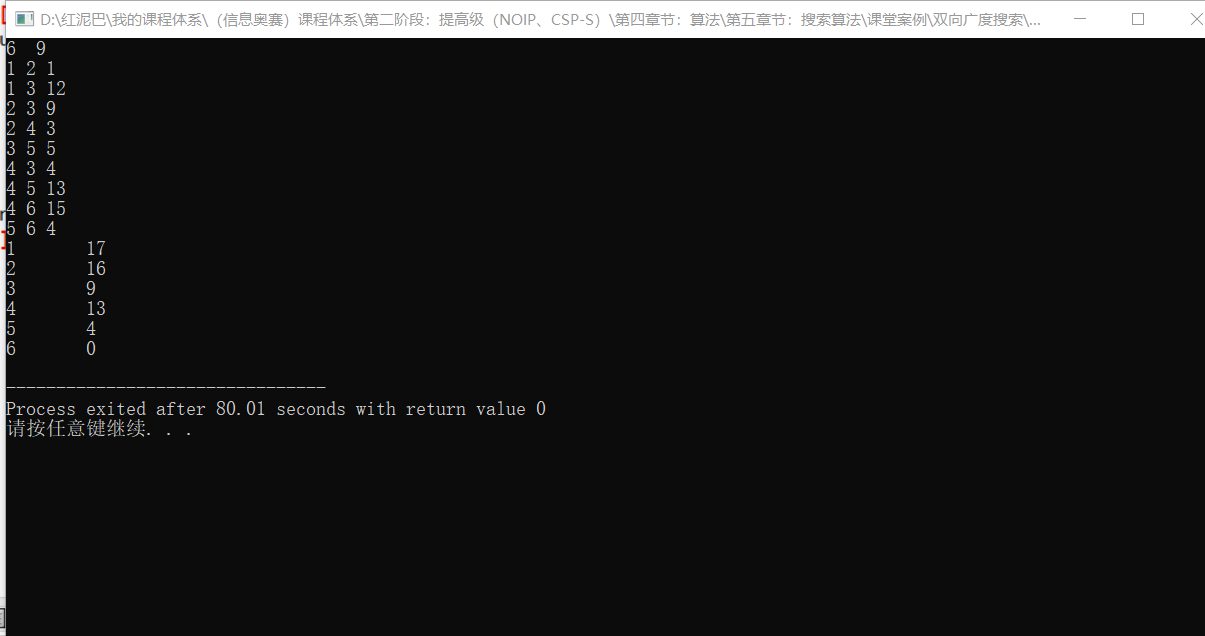
根据计算结果，可知节点3的g(3)+h(3)=10+9=19；节点4的g(4)+h(4)=4+13=17。显然，选择节点4更接近目标点。

知道了优先策略以及计算方式。下面具体演示，看如何得到最终结果。

• 准备好优先队列。用节点、节点离源点距离、节点离目标点的距离三元素构建一个三元信息组，存入队列。初始存入节点1的三元信息(1,0,0)。

  Tips： 如果节点1到节点6的最短距离为INF，则表示两者之间没有路径。

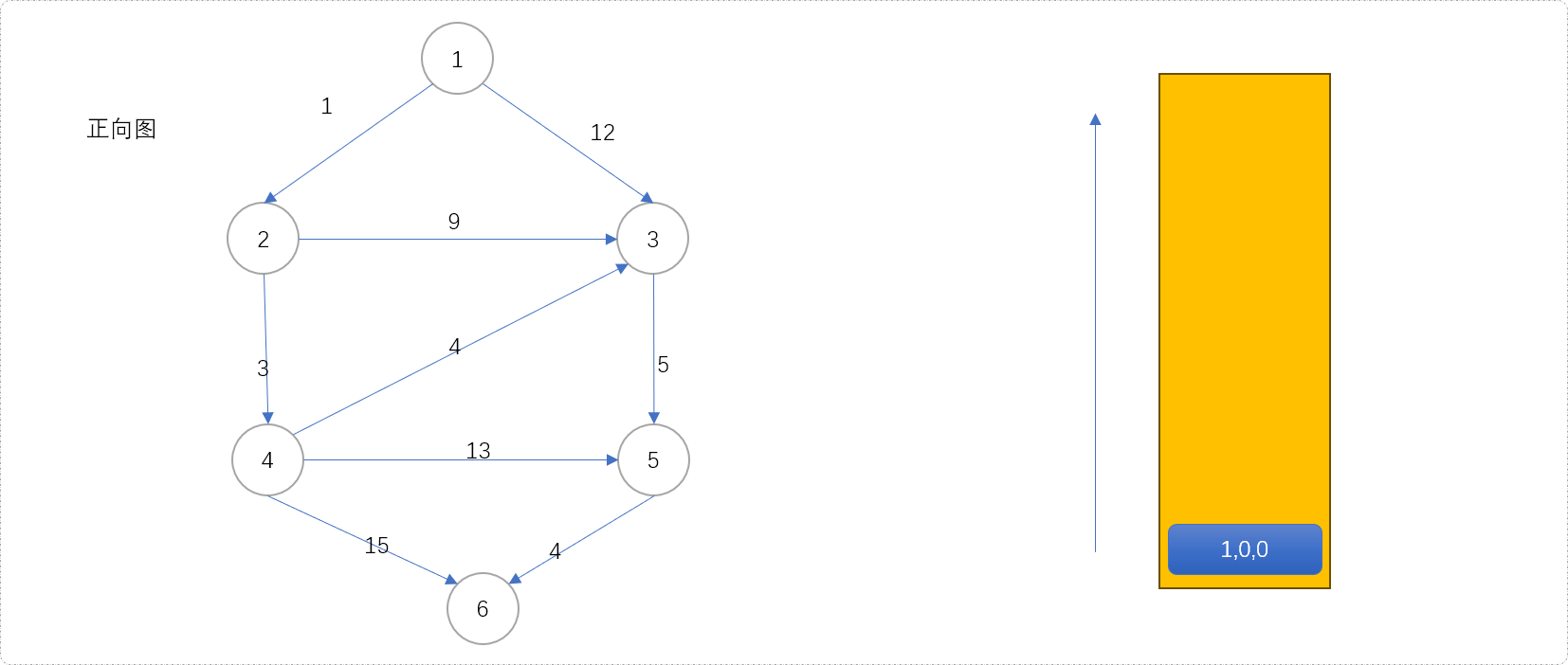
• (1,0,0)出队列，扩展2、3号节点，分别计算2、3号节点的三元组信息(2,1,16)、(3,12,9)且压入队列。

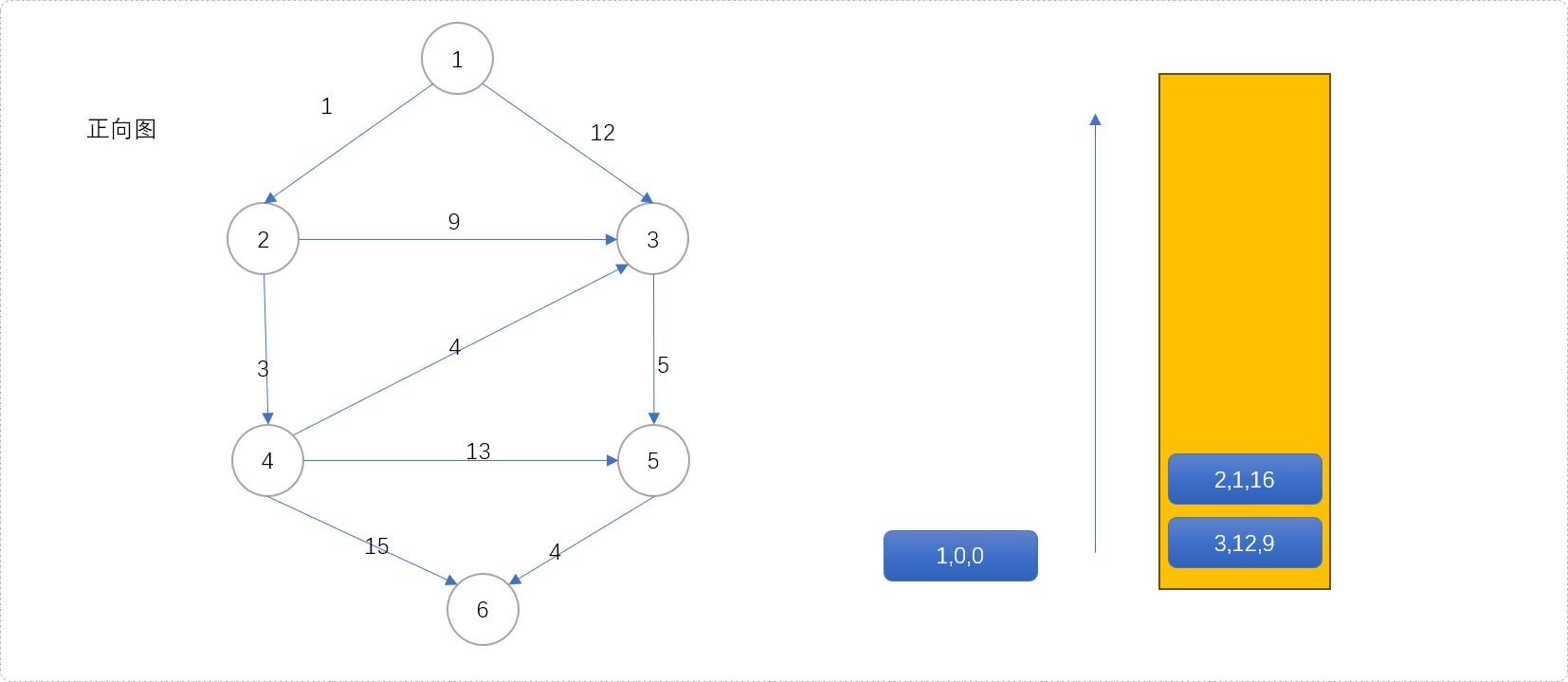
• 根据优先策略，(2,1,16)第一次出队列，其值1+16=17即为源点经过节点2到目标点的最短距离，扩展(3,10,9)和(4,4,13)。

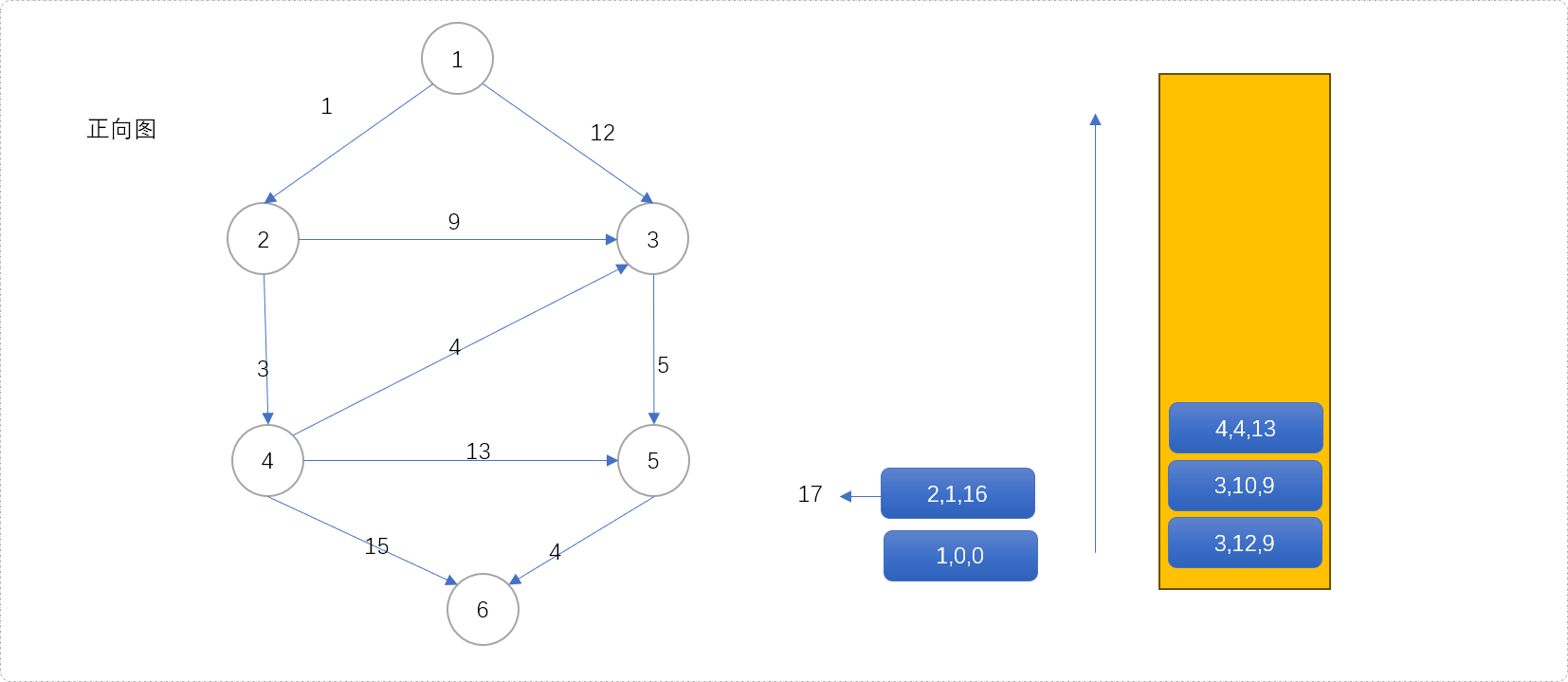
• (4,4,13)出队列，得到源点经过4到达目标点的最短距离为17。扩展(3,8,9)、(5,17,4)、(6,19,0)。从下图可知，节点3会入队列三次。因为节点3有三个入度，意味着有三个节点可以经过它进入下一个位置，即有三次扩展机会。

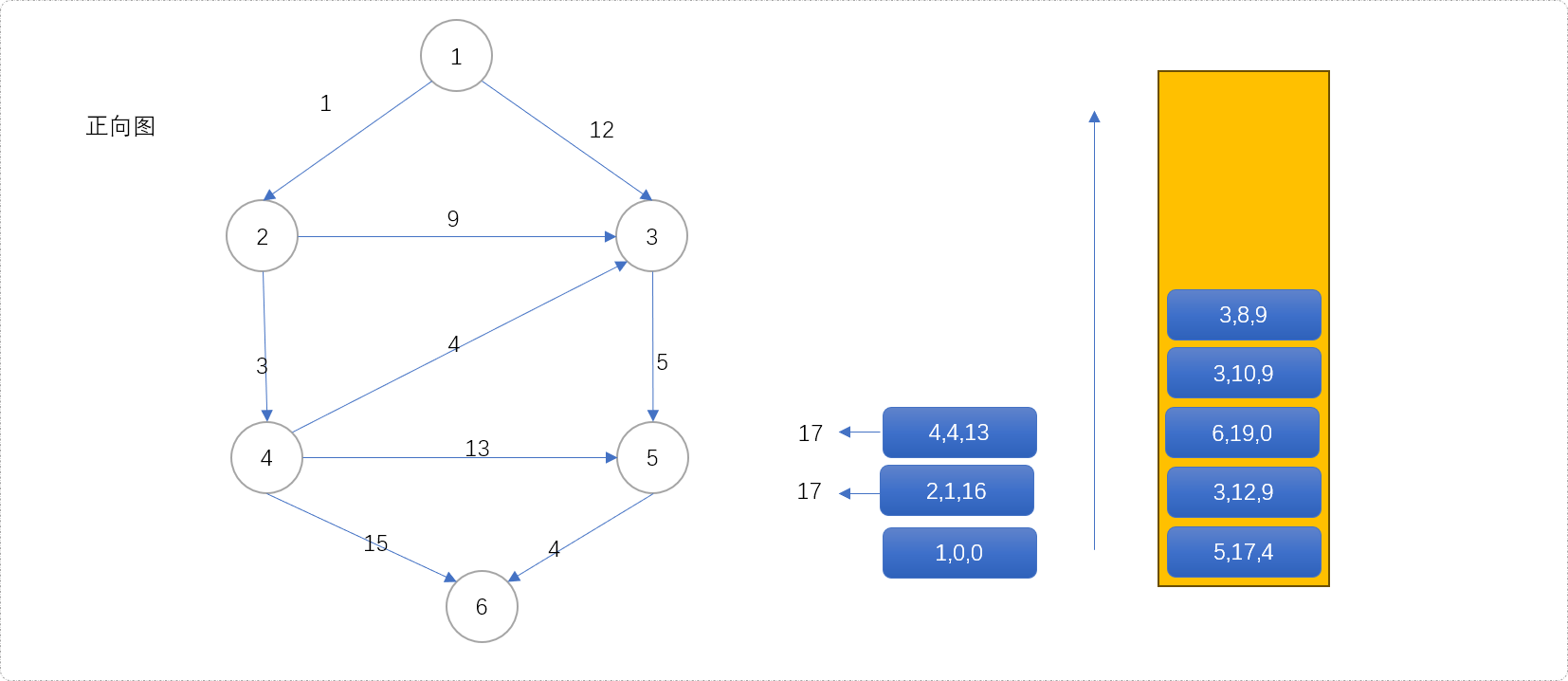
• (3,8,9)第一次出队列，意味着源点经过3号节点到达目标点的最短距离为17。原因很简单，根据队列的优先策略，只有当g(x)+h(x)值最小时，才有机会出队列，而这两个值，一个表示离源点最优值，一个是表示离目标点的最优值，两者之和一定是源点经过此点到达目标点的最优值。此时，扩展(5,13,4)入队列。

  观察可得，节点3会出队列三次，同时扩展节点5进入三次队列，这样，不会漏掉任何一条路径。在迪杰斯特拉算法中，如果节点3当前值为15，扩展后的值为17，是不会再入队列的，迪杰斯特拉算法中存储的永远是比上一次更优的值。

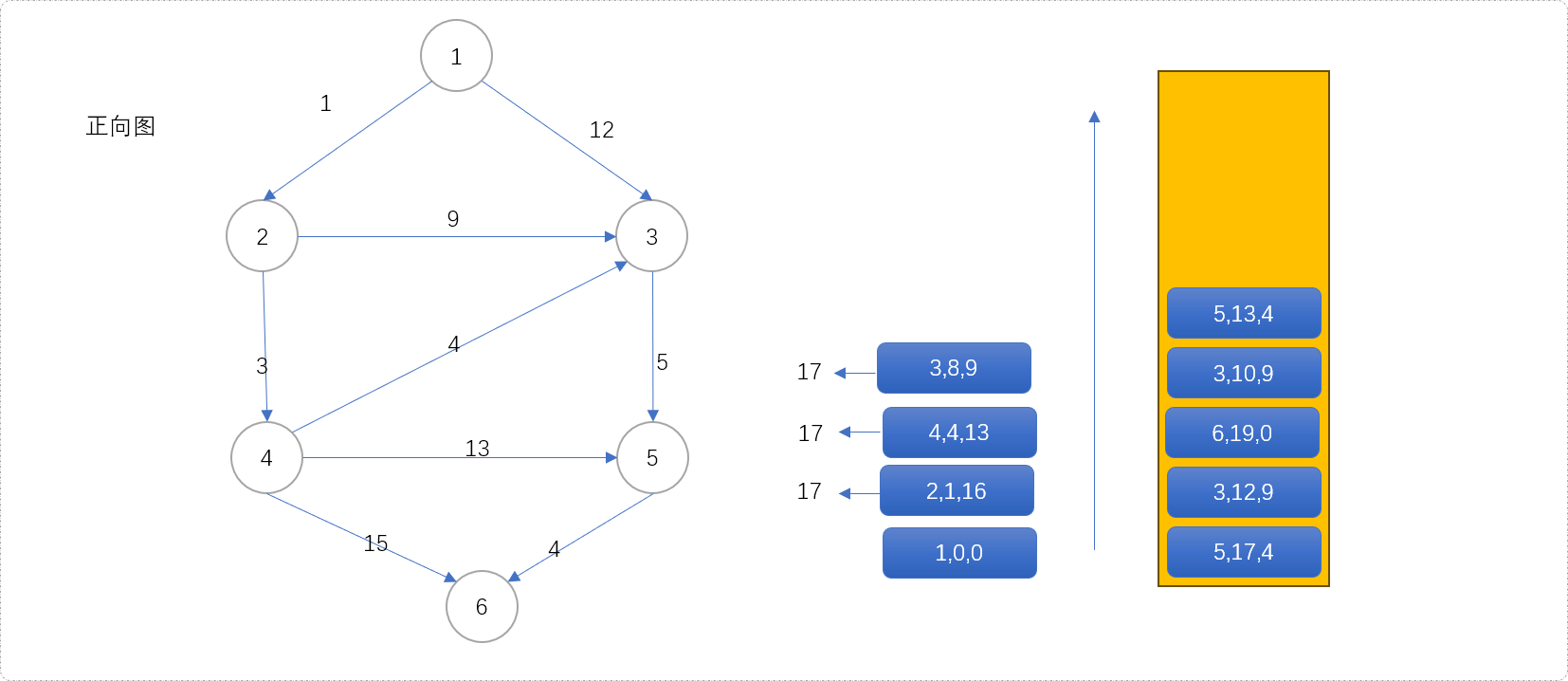
• (5,13,4)第一次出队列，得到源点经过5到达目标点的最短距离是17。同时扩展(6,17,0)入队列。

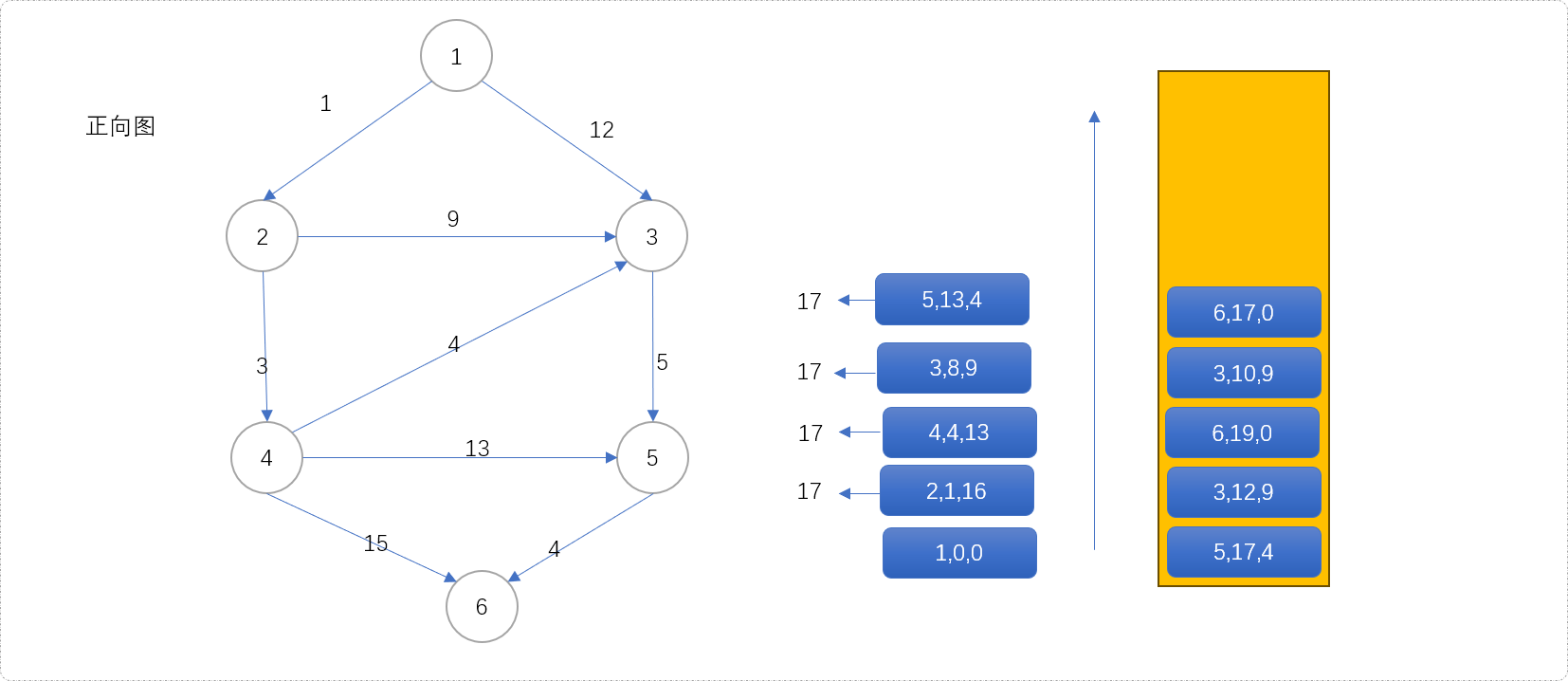
• (6,17,0)第一次出队列，源点到目标点的最短距离为17。

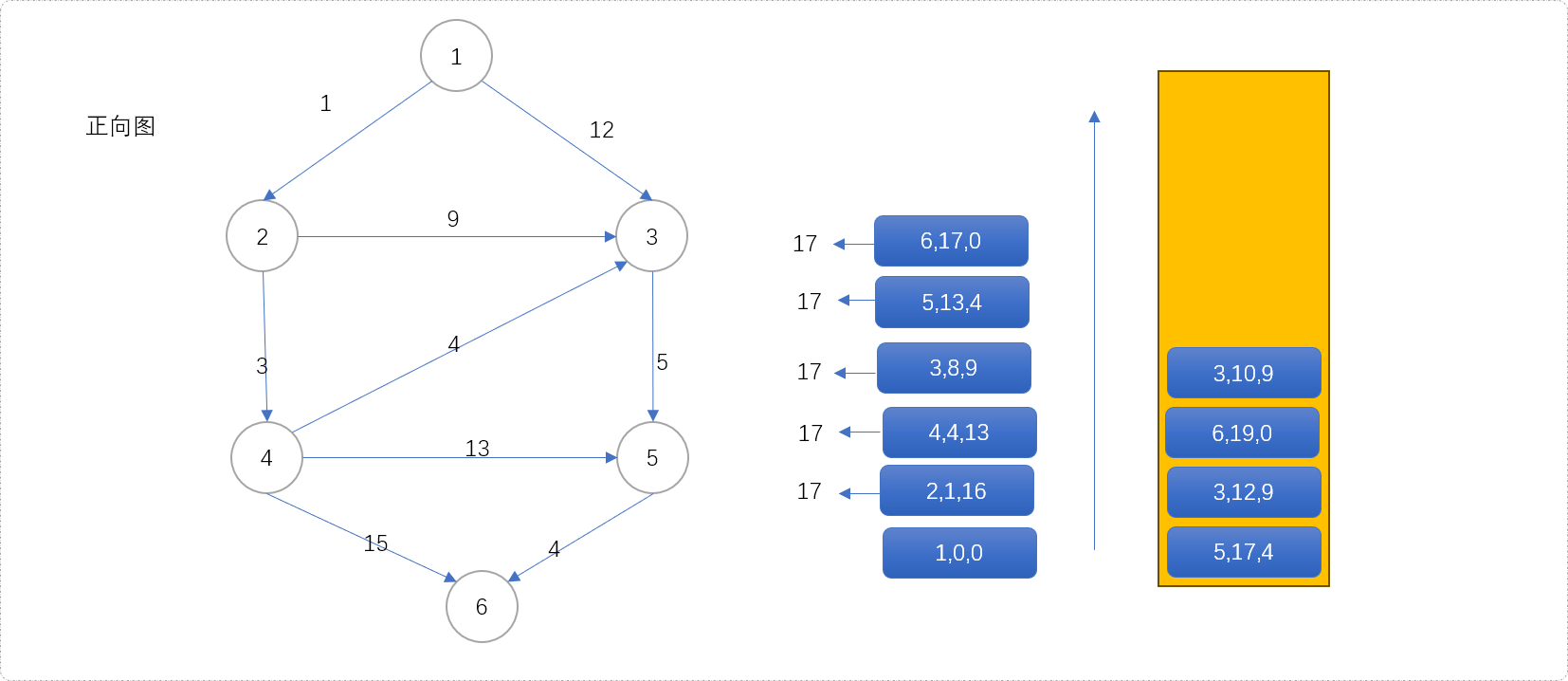
• (3,10,9)第二次出队列，则得到源点经过3到达目标点的次短距离为19。

  (6,19,0)第二次出队列时，得到源点到目标点次最短距离为19，其实和前分析迪杰斯特拉算法的更新信息是一致的。只是迪杰斯特拉算法会漏掉一些路径，A*算法不会。

  如下图是当整个算法结束后得到的出队结果，可以看到节点5入了4次队列，出了4次队列。说明源点经过节点5到少有4条不同路径到达目标点。分别是1->3->5->6、1->2->3->5->6、1->2->4->3->5->6、1->2->4->5->6。

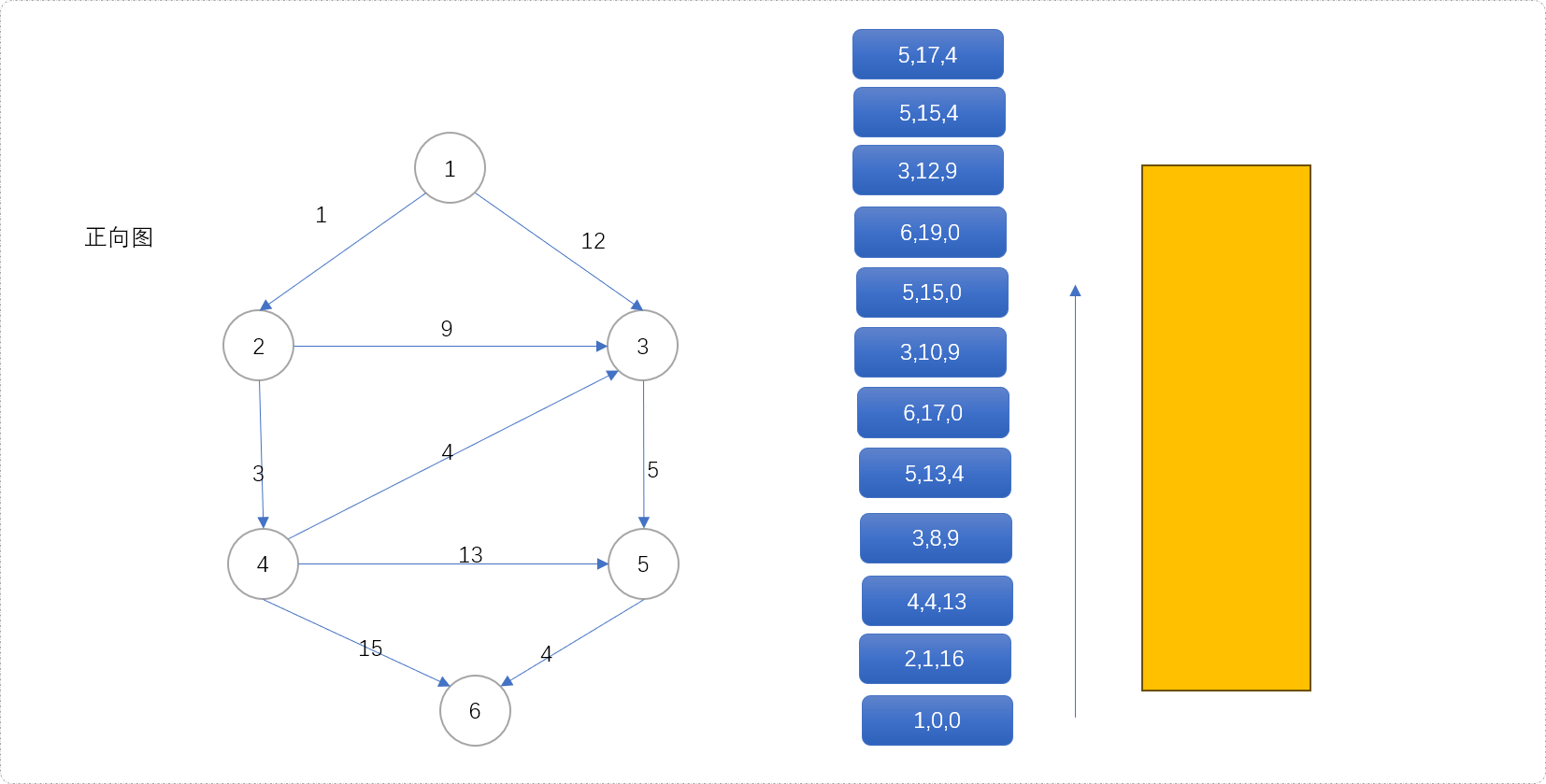
通过上述分析，可以得到一个结论：

当目标节点从队列中第i次出队时，就是离源点的第i次最短距离。

完整代码如下所示：

#include <bits/stdc++.h>
#define MAX 300000 + 50
#define INF 0x3f3f3f3f
using namespace std;

/*
*顶点类型
*/
struct Ver {
	//编号
	int vid;
	//离终点的最短距离
	int toDis=INF;
	//离源点的最短距离
	int fromDis=INF;
	//正向图头指针
	int head=0;
	//反向图头指针
	int rhead=0;

	const bool operator<(const Ver & ver) const {
		return this->toDis>ver.toDis;
	}

} vers[MAX];
//顶点和边数
int n,m;
//边类型
struct Edge {
	//邻接点
	int to;
	//下一个边
	int nex;
	//权重值
	int val;
}  edges[MAX];

//边索引
int tot=0;

//添加正向边
void addEdge(int type,int f, int t, int w) {
	edges[++tot].to = t;
	edges[tot].val = w;
	if(type==0) {
		edges[tot].nex = vers[f].head;
		vers[f].head= tot;
	} else {
		edges[tot].nex = vers[f].rhead;
		vers[f].rhead= tot;
	}
}

//构建图
void buildGraph() {
	for( int i=1; i<=n; i++ )vers[i].vid=i;
	int f,t,w;
	for(int i = 1; i <= m; ++i) {
		cin >> f >> t >> w;
		addEdge(0,f,t,w);
		addEdge(1,t,f,w);
	}
}

/*
*
*对原图的反图求各节点到目标节点的最短距离
*/
void dijkstra(int s) {
	//优先队列
	priority_queue<Ver>  priQue;
	vers[s].toDis=0;
	//初如化队列
	priQue.push( vers[s] );
	while( !priQue.empty()  ) {
		//取头顶点
		Ver u=priQue.top();
		//删除头顶点
		priQue.pop();
		//扩展子节点
		for( int i=u.rhead; i!=0; i=edges[i].nex ) {
			Ver v=vers[  edges[i].to ];
			if( v.toDis> edges[i].val+u.toDis  ) {
				//更新
				v.toDis= edges[i].val+u.toDis;
				vers[  edges[i].to ]=v;
				priQue.push(v);
			}
		}
	}
}

template<typename T>
struct Cmp {
	bool operator()(T & ver1,T & ver2) {
		return ver1.fromDis+ver1.toDis>ver2.fromDis+ver2.toDis;
	}
};

//A* 算法
int nums[MAX]= {0};
int astar(int s,int e,int k) {
	//对反向图求最短距离 
	dijkstra(e);
	//初始化计时器 
	if(vers[s].toDis==INF)return -1;
	for(int i=1; i<=n; i++)nums[i]=0;
	priority_queue<Ver,vector<Ver>,Cmp<Ver>> myq;
	//初始化队列
	vers[s].fromDis=0;
	vers[s].toDis=0;
	myq.push(vers[s]);
	while( !myq.empty() ) {
		//出队列
		Ver u=myq.top();
		myq.pop();
		//计算节点出队列的次数
		nums[u.vid]++;
		//如果次数和k值相同，且当前出队列节点是目标节点 
		if( nums[u.vid]==k && u.vid==e ) {
			//找到答案 
			return u.fromDis+u.toDis;
		}
		//如果计数器值大于K 
		if( nums[u.vid]>k )continue;
		//扩展子节点
		for( int i=u.head; i!=0; i=edges[i].nex ) {
			Ver v=vers[  edges[i].to ];
			v.fromDis=edges[i].val+u.fromDis;
			vers[  edges[i].to ]=v;
			myq.push(v);
		}
	}
	return -1;
}

void show() {
	for(int i=1; i<=n; i++) {
		cout<<vers[i].vid<<"\t"<<vers[i].toDis<<endl;
	}
}

int main() {
	cin>>n>>m;
	buildGraph();
	int res= astar(1,6,3);
	cout<<res;
//	show();
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150

3. 总结

本文讲解有向图如何使用A*算法。记住，当选择很多时，预估出每一个选择要付出的代价，可以减少不必要的损失。人生如此，代码如此。