Pytorch学习笔记（五）——CNN中卷积和池化操作后的特征图大小计算方法_torch输出卷积后的结果

特别的：
当计算尺寸不被整除时，卷积向下取整，池化向上取整。（只在GoogLeNet中遇到过。）
一般的：
卷积池化均向下取整

一、卷积操作

假设：
设输入图像尺寸为WxW，卷积核尺寸为FxF，步幅为S，填充为P,经过该卷积层后输出的图像尺寸为NxN,计算公式为：
$$N=\frac{W-F+2P}{S}+1$$
设输入图像尺寸为WxH，卷积核的尺寸为FxF，步幅为S，图像深度(通道数)为C，填充为P，则：
$$W=\frac{W-F+2P}{S}+1$$
$$H=\frac{H-F+2P}{S}+1$$
如果无填充，公式可以简化为“
WxW:
$$N=\frac{W-F}{S}+1$$
WxH:
$$W=\frac{W-F}{S}+1$$
$$H=\frac{H-F}{S}+1$$
也可使用以下公式计算：

二、池化操作

设输入图像尺寸为WxH，其中W:图像宽，H:图像高，卷积核的尺寸为FxF，S:步长，当计算池化操作时，参数量为0，且由于没有padding操作：

池化后输出图像大小：
WxW:
$$N=\frac{W-F}{S}+1$$
WxH:
$$W=\frac{W-F}{S}+1$$
$$H=\frac{H-F}{S}+1$$

三、实战

3.1.卷积计算例1

假设我们有如下一个3x3的input，Kernel大小为2x2，其中stride为1，padding为0，卷积后的大小和结果如output

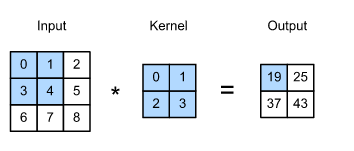
现在我们来看卷积操作是如何得到这个结果的：
1.计算卷积后输出特征图的大小：
将W=2,F=2,P=0,S=1带入如下公式
$$N=\frac{W-F+2P}{S}+1=\frac{3-2+2\times 0}{1}+1=2$$
由于N=2，故而我们的输出将会是一个2x2的矩阵。
2.计算矩阵的值。
在二维互相关运算中，卷积窗口从输入张量的左上角开始，从左到右、从上到下滑动。 当卷积窗口滑动到新一个位置时，包含在该窗口中的部分张量与卷积核张量进行按元素相乘，得到的张量再求和得到一个单一的标量值，由此我们得出了这一位置的输出张量值。 在如上例子中，输出张量的四个元素由二维互相关运算得到，这个输出高度为 2 、宽度为 2 ，如下所示：
$$\begin{gathered} 0\times 0+1\times 1+3\times 2+4\times 3=19 \\ 1\times 0+2\times 1+4\times 2+5\times 3=25 \\ 3\times 0+4\times 1+6\times 2+7\times 3=37 \\ 4\times 0+5\times 1+7\times 2+8\times 3=43 \end{gathered}$$
用代码实现的话，如下：

def corr2d(X, K):  #@save
    """计算二维互相关运算。"""
    h, w = K.shape
     
     #设置输出矩阵的大小
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1)) 

    #卷积核移动求值
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
    return Y
1
2
3
4
5
6
7
8
9
10
11
12

3.2.卷积计算例2

如例1的3x3的input，Kernel大小为2x2，其中宽度方向stride为2，高度方向的stride为3，padding为1，卷积后的大小和结果如output。

现在我们来看卷积操作是如何得到这个结果的：
1.计算卷积后输出特征图的大小：
将W=3,F=2,P=1,S_W=2,S_H=3带入如下公式
$$\begin{gathered} W=\frac{W-F+2P}{S_W}+1=\frac{3-2+2\times 1}{2}+1=2.5 \\ H=\frac{H-F+2P}{S_H}+1=\frac{3-2+2\times 1}{3}+1=2 \end{gathered}$$
其中，我们向下取整得W=2，且H=2，故而我们的输出仍然将会是一个2x2的矩阵。
2.计算矩阵的值。
在二维互相关运算中，卷积窗口从输入张量的左上角开始，从左到右、从上到下滑动。 当卷积窗口滑动到新一个位置时，包含在该窗口中的部分张量与卷积核张量进行按元素相乘，得到的张量再求和得到一个单一的标量值，由此我们得出了这一位置的输出张量值。 在如上例子中，输出张量的四个元素由二维互相关运算得到，这个输出高度为 2 、宽度为 2 ，如下所示：
$$\begin{gathered} 0\times 0+0\times 1+0\times 2+0\times 3=0 \\ 0\times 0+0\times 1+1\times 2+2\times 3=8 \\ 0\times 0+6\times 1+0\times 2+0\times 3=6 \\ 7\times 0+8\times 1+0\times 2+0\times 3=8 \end{gathered}$$

3.3.池化操作例1

与卷积层类似，汇聚层运算符由一个固定形状的窗口组成，该窗口根据其步幅大小在输入的所有区域上滑动，为固定形状窗口（有时称为 池化窗口*）遍历的每个位置计算一个输出。 然而，不同于卷积层中的输入与卷积核之间的互相关计算，汇聚层不包含参数。 相反，池运算符是确定性的，我们通常计算池化窗口中所有元素的最大值或平均值。这些操作分别称为 *最大汇聚层 （maximum pooling）和 平均汇聚层 （average pooling）。

在这两种情况下，与互相关运算符一样，池化窗口从输入张量的左上角开始，从左到右、从上到下的在输入张量内滑动。在池化窗口到达的每个位置，它计算该窗口中输入子张量的最大值或平均值，具体取决于是使用了最大汇聚层还是平均汇聚层。
我们只讲一下最大pooling操作，其操作是选取窗口中值最大的单元。

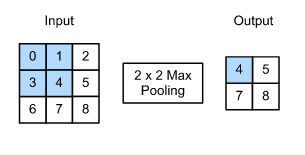
1.计算池化后输出特征图的大小：
将W=3,F=2,S=1，带入如下公式
$$N=\frac{W-F}{S}+1=\frac{3-2}{1}+1=2$$
故而我们的输出将会是一个2x2的矩阵。
2.计算矩阵的值。

$$\begin{gathered} max(0,1,3,4)=4 \\ max(1,2,4,5)=5 \\ max(3,4,6,7)=7 \\ max(4,5,7,8)=8. \end{gathered}$$
参考：
图像卷积和池化操作后的特征图大小计算方法