NOIP2017 提高组奶酪（DFS、BFS、并查集）一题三解_p3958 [noip2017 提高组] 奶酪

作者：IT小白 | 2024-07-06 08:59:00

踩

p3958 [noip2017 提高组] 奶酪

原文链接：NOIP真题第三讲：奶酪

题目来源：2017 年 NOIP 提高组第一题

本题考察点：【DFS、BFS、并查集】

一、题目及链接

题目链接：

https://www.luogu.com.cn/problem/P3958

题意：老鼠是否可以从下表面的空洞一直沿着空洞走到上表面，如果可以，输出Yes，否则输出No；

二、问题分析

该题可以通过搜索来实现，找出所有的入口（即与下表面相切或相交的空洞）作为搜索的入口，在搜索的过程中，对已经搜过的空洞进行标记，每搜到一个空洞，判断是否为出口（即该空洞与上表面相交或相切），如果是，输出Yes，然后return，否则继续搜索，直到以所有入口为起点搜索完，还未找到出口，则说明不能从入口到出口，输出No并返回即可。

该问题还可以使用并查集来解决，暴力遍历任意两个空洞，检查，如果两个空洞相交或相切，则合并，遍历结束后，再分别遍历所有入口和出口，如果任意两个入口和出口是并查集中的同一合集，则说明可以从入口到出口，输出Yes，否则输出No；

三、问题解决

Q1: 如何判断一个空洞为入口或出口呢？

A1：如果为入口，则空洞的纵坐标z小于等于半径r；如果为出口，则空洞的纵坐标z加上半径r大于等于高度h；

Q2: 如何判断两个空洞是否相交或相切？

A2: 两个空洞的球心坐标距离小于等于半径的2倍即说明相交或相切。

Q3: 搜索过程中如何标记哪些点已经被搜索过呢？

A3: 用bool类型的vis数组标记。

下面我会分别使用DFS、BFS和并查集实现一次，请结合代码和注释一起阅读和思考。

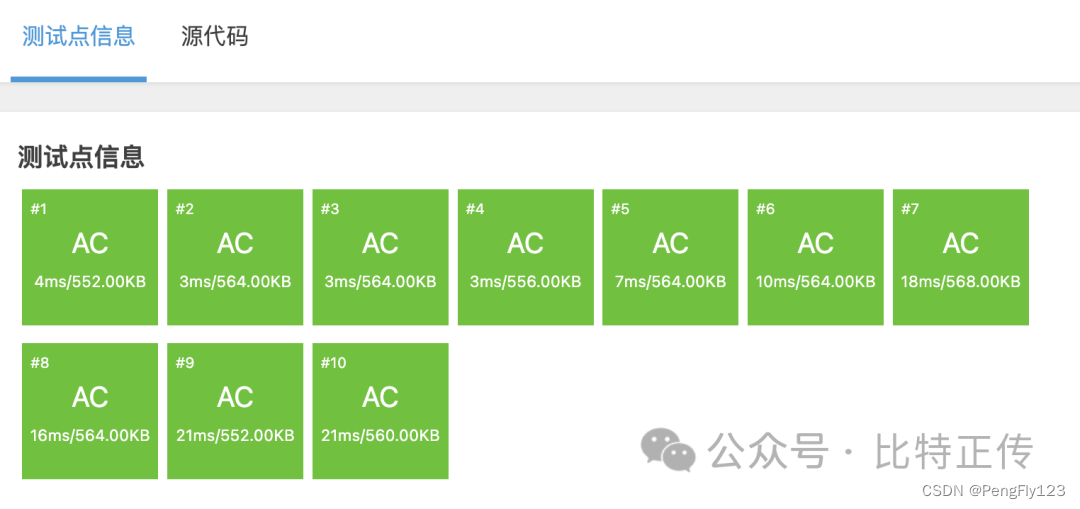
四、AC Code

DFS


#include "bits/stdc++.h"
using namespace std;
const int N = 1e3+7;
long long t, n, h, r;
bool vis[N];
 
struct Node{  // 球心坐标
    int x, y ,z;
}a[N];
 
// 计算两点之间的距离，为避免小数，返回距离的平方（即省去开根号）
long long dist(int idx1, int idx2) {
    return pow(a[idx1].x-a[idx2].x, 2) + pow(a[idx1].y-a[idx2].y, 2) +
    pow(a[idx1].z-a[idx2].z, 2);
}
 
// 检查两个空洞是否相切，相切或相交返回true，否则返回false
bool check(int idx1, int idx2) {
    long long d = 4*r*r;
    if(dist(idx1, idx2) <= d) return true;
    return false;
}
 
// 判断是否为入口
bool isIn(int idx) {
    return a[idx].z <= r;
}
// 判断是否为出口
bool isOut(int idx) {
    return a[idx].z + r >= h;
}
// 从第idx个空洞是否可以搜索到出口，如果可以搜索到出口，返回true，否则返回false
bool dfs(int idx) {
    if(vis[idx]) return false;  // 已经被搜索过，返回false
    if(isOut(idx)) return true;  // 搜索到了出口，返回true
    vis[idx] = true;  // 标记
    for(int i=1; i<=n; i++) {
        if(vis[i]) continue;  // 搜索过的不再搜索
        if(check(idx, i) && dfs(i)) return true;  // 如果相交且能搜索出口，返回true
    }
    return false;
}
 
int main(){
    cin >> t;
    while(t--) {
        cin >> n >> h >> r;
        memset(vis, false, sizeof vis);
        for(int i=1; i<=n; i++) {
            cin >> a[i].x >> a[i].y >> a[i].z;
        }
        bool isTrue = false;
        for(int i=1; i<=n; i++) {
            // 如果没有被访问过且是入口且搜索到了出口，则输出YES，并结束本组数据，看下一组数据
            if(!vis[i] && isIn(i) && dfs(i)) {
                cout << "Yes" << endl;
                isTrue = true;
                break;
            }
        }
        if(!isTrue) cout << "No" << endl;  // 如果没输出YES，则输出NO
    }
    return 0;
}

BFS


#include "bits/stdc++.h"
using namespace std;
const int N = 1e3+7;
long long t, n, h, r;
bool vis[N];
queue<int> q;
 
struct Node{  // 球心坐标
    int x, y ,z;
}a[N];
 
// 计算两点之间的距离，为避免小数，返回距离的平方（即省去开根号）
long long dist(int idx1, int idx2) {
    return pow(a[idx1].x-a[idx2].x, 2) + pow(a[idx1].y-a[idx2].y, 2) +
    pow(a[idx1].z-a[idx2].z, 2);
}
 
// 检查两个空洞是否相切，相切或相交返回true，否则返回false
bool check(int idx1, int idx2) {
    long long d = 4*r*r;
    if(dist(idx1, idx2) <= d) return true;
    return false;
}
 
// 判断是否为入口
bool isIn(int idx) {
    return a[idx].z <= r;
}
// 判断是否为出口
bool isOut(int idx) {
    return a[idx].z + r >= h;
}
 
void bfs() {
    while(!q.empty()) {
        int head = q.front();  // 拿出队头
        if(isOut(head)) {   // 如果队头为出口
            cout << "Yes" << endl; // 输出并返回
            return;
        }
        q.pop();  // 弹出队头
        for(int i=1; i<=n; i++) {
            if(!vis[i] && check(i, head)) {  // 没有访问并相交
                vis[i] = true;
                q.push(i);  // 加入队列
            }
        }
    }
    cout << "No" << endl;
    return ;
}
 
int main(){
    cin >> t;
    while(t--) {
        cin >> n >> h >> r;
        memset(vis, false, sizeof vis);
        while(!q.empty()) q.pop();
        for(int i=1; i<=n; i++) {
            cin >> a[i].x >> a[i].y >> a[i].z;
            if(isIn(i)) {  // 将所有的入口放入队列
                q.push(i);
                vis[i] = true;  // 并标记
            }
        }
        bfs();
    }
    return 0;
}

并查集


#include "bits/stdc++.h"
using namespace std;
const int N = 1e3+7;
long long t, n, h, r;
unordered_set<int> st;
struct Node{  // 球心坐标
    int x, y ,z;
}a[N];
 
int p[N];  // 并查集中的parent数组，p[i]表示i的父亲，初始时p[i]等于i，表示自己是自己的父亲
// 计算两点之间的距离，为避免小数，返回距离的平方（即省去开根号）
long long dist(int idx1, int idx2) {
    return pow(a[idx1].x-a[idx2].x, 2) + pow(a[idx1].y-a[idx2].y, 2) +
    pow(a[idx1].z-a[idx2].z, 2);
}
 
// 检查两个空洞是否相切，相切或相交返回true，否则返回false
bool check(int idx1, int idx2) {
    long long d = 4*r*r;
    if(dist(idx1, idx2) <= d) return true;
    return false;
}
 
// 寻找child的根父亲节点，并查集的模板
int findFather(int child) {
    if(child == p[child]) return p[child];
    p[child] = findFather(p[child]);  // 并查集的压缩路径
    return p[child];
}
 
// 合并两个空洞为一个集合，并查集的模板
void unionFind(int idx1, int idx2) {
    int p1 = findFather(idx1), p2 = findFather(idx2);  // 找到各自的根父亲
    if(p1 != p2) p[p1] = p2;  // 如果两个根父亲不是一个节点，则合并
    return;
}
 
// 判断是否为入口
bool isIn(int idx) {
    return a[idx].z <= r;
}
// 判断是否为出口
bool isOut(int idx) {
    return a[idx].z + r >= h;
}
// 初始化st为空，且p数组中p[i]=i;
void init() {
    for(int i=1; i<=n; i++) p[i] = i;
    st.clear();
}
 
int main(){
    cin >> t;
    while(t--) {
        cin >> n >> h >> r;
        init();  // 更新p数组
        for(int i=1; i<=n; i++) {
            cin >> a[i].x >> a[i].y >> a[i].z;
        }
        for(int i=1; i<n; i++) {
            for(int j=i+1; j<=n; j++) {
                if(check(i, j)) unionFind(i, j);  // 搜索任意两个空洞，如果相切或相交，合并
            }
        }
        for(int i=1; i<=n; i++) {
            if(isIn(i)) {  // 如果第i个空洞为入口，则将其根父节点加入到st集合中
                int f = findFather(i);  // 找到根父节点
                st.insert(f);  // 插入st
            }
        }
        bool isTrue = false;  // 是否找到相连的入口和出口
        for(int i=1; i<=n; i++) {  // 遍历所有空洞
            // 如果是入口且该节点和出口有共同的根父节点，则一定可以到出口
            if(isOut(i) && st.count(findFather(i)) > 0) {
                cout << "Yes" << endl;
                isTrue = true;
                break;
            }
        }
        if(!isTrue) cout << "No" << endl;  // 如果isTrue为false，说明不能从入口到出口，输出NO；
    }
    return 0;
}

五、往期文章

NOIP真题第二讲：摆花

NOIP 真题第一讲：FBI 树