- 1vscode推送gitee方法_vscode 推送到git
- 2常见的排序算法_14.请写出长度为len顺序表a的比较排序伪算法?
- 3内网渗透——macOS上搭建Web服务器_mac本地搭建公网
- 4linux系统配置php环境,linux下php环境的搭建
- 5【Java基础】Java中不能被实例化的类 -- p267_不能实例化类型怎么解决
- 6随机森林分类器_随机森林的重要属性之一:estimators_
- 7跑yolov3时,出现RuntimeError: There were no tensor arguments to this function (e.g., you passed。。。如何解决_notimplementederror: there were no tensor argument
- 8Java编程环境搭建_java编程环境如何搭建
- 9AWS实验|实验 4 - 使用 EBS [Lab 4 - EBS]_sudo mkfs -t ext3 /dev/sdf
- 10scanf和scanf_s函数详解_scanf_s与scanf的区别
人工智能之深度学习_人工智能深度学习
赞
踩
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助
一、神经网络的思想
1.1神经网络和深度学习
1.人工智能、深度学习、机器学习的关系?
人工智能 > 机器学习 > 深度学习
- 1
2.深度学习以神经网络为出发点
神经元
(1)神经元形成网络;
(2)对于从其他神经元传递过来的信号,如果它们的和不超过某个固定大小的值(阙值),则神经元不做出任何反应;
(3)对于从其他神经元传递过来的信号,如果它们的和超过某个固定大小的值(阙值),则神经元做出反应(称为点火),向另外的神经元传递固定强度的信号;
(4)在(2)和(3)中,从多个神经元传递过来的信号之和中,每个信号对应的权重不同;
3.用神经网络实现的人工智能
能够自己学习过去的数据;
4.“人教导机器”类型的的人工智能问题
“人教导机器”类型的的人工智能无法胜任图像、语音的模式识别;
1.2神经元工作的数学表示
1.神经元点火的结构
(1)来自其他神经元的信号之和称为神经元的输入;
(2)如果这个神经元之和超过神经元固有的阙值则点火;
(3)神经元的输出信号可以用数字信号0和1表示,即使有多个输出端,其值也是同一个;
2.用数学式表示神经元点火的结构
(1)输入信号:有两种信息表示:
无输入信号:x=0
有输入信号:x=1
(2)输出信号:有两种信息表示:
无输入信号:y=0
有输入信号:y=1
即使有多个输出端,输出信号的大小也相同;
3.点火的判定条件
(1)输入信号之和: w1x1 + w2x2 + w3x3
式中w1、w2、w3是x1、x2、x3的权重(weight)
(2)判定条件
无输入信号:y=0 :w1x1 + w2x2 + w3x3 < r
有输入信号:y=1 :w1x1 + w2x2 + w3x3 >=r
式中 r 神经元固有的阙值
3.点火条件的图形表示


1.3激活函数:将神经元的工作一般化
1.激活函数
点火的式子:y = u(w1x1 + w2x2 + w3x3 -r) u 是单位阶跃函数,
将该式一般化: y = a(w1x1 +w2x2 + w3x3 -r)----激活函数
2.神经元和神经单元的不同点
| 神经元 | 神经单元 | |
|---|---|---|
| 输出值y | 0或1 | 模型允许的任意数值 |
| 激活函数 | 单位阶跃函数 | 由分析者给出,其中著名的是Sigmoid函数 |
| 输出的解释 | 点火与否 | 输出单元的兴奋度、反应度、活性度 |
Sigmoid函数:

3.偏置
y = a(w1x1 + w2x2 + w3x3 -r)
-> y = a(w1x1 + w2x2 + w3x3 + b) (b --偏置)
加权输入:
z = w1x1 + w2x2 + w3x3 + b ---->z = w1x1 + w2x2 + w3x3 + b*1
1.4什么是神经网络
将神经单元的多个输入x1,x2,…,xn整理为加权输入z
z = w1x1 + w2x2 + … +wnxn+ b
其中w1,w2…wn为权重,b为偏置,n为输入的个数;神经单元通过激活函数a(z),根据加权输入z输出y
y = a(z) 将这样的神经单元连成网络状,就形成了神经网络;
1.阶层型神经网络

(1)按照 层(layer) 划分神经单元,通过这些神经单元处理信号,然后通过输出层输出结果;
(2)前一层的神经单元与后一层的所有神经单元都有箭头连接,这样的层构造称为 全连接层;
(3)神经网络各层的职责
输入层:负责读取给予神经网路的信息。属于这个层的神经单元没有输入箭头,是简单的神经单元,只是将从数据得到的值原样输出;
隐藏层:隐藏层的神经单元执行信息处理操作。在神经网络中,这是实际处理信息的部分;
输出层:输出层和印尼擦高层一样执行信息处理操作,并显示神经网络计算出的结果,也就是整个神经网路的输出;
深度学习就是叠加了很多层的神经网络。
1.5网络自学习的神经网络
(1)神经网络的参数确定方法分为有监督学习和无监督学习;
(2)有监督学习:为了确定神经网络的权重和偏置,实现给予数据,这些数据称为学习数据;
(3)根据给定的数据确定权重和偏置,称为学习;
(4)计算神经网络得出的预测值和正解的为误差,确定使得误差总和达到最小的权重和偏置,这在数学上称模型的最优化;
(5)针对全部学习数据,计算预测值与正解的误差的平方(称为平方误差),在相加,得到的误差总和称为代价函数,用Ct表示;
二、神经网络的数学基础(上)
2.1神经网络所需的函数
1.一次函数
(1)单个自变量: y = ax + b (a、b为常数,a !=0)
a-----斜率 b-----截距
(2)两个自变量:y = ax1 + b*x2 + c(a、b、c为常数,a、b !=0)
(3)在神经网络中,神经单元的加权输入可以表示为一次函数关系,
z = w1x1 + w2x2 + w3x3 + b
2.二次函数
(1)单个自变量:y = ax^2 + bx + c (a、b、c为常数,a !=0)
(2)两个自变量:y = ax1^2 + bx1x2 + cx2^2 + q1x1 + q2x2 + r
(3)实际的神经网络需要处理更多变量的二次函数;
3.单位阶跃函数

4.指数函数

5.正态分布的概率密度函数

正态分布是服从概率密度函数 f(x)的概率分布;
用计算机实际确定神经网路时,必须设定权重和偏置的初始值,使用正态分布的随机数,容易取得好结果;
2.2有助于理解神经网络的数列和递推公式
1.数列
(1)数列是数的序列; (2)数列的每一个数称为项
2.数列的通项公式
将数列的第 n 项用一个关于 n 的式子表示出来,这个式子即该数列的通项公式;
3.数列与递推关系式
一般地,如果已知首先a1,以及相邻两项 an,an+1的关系式,就可以确定这个数列,这个关系式称为递推关系式;
4.联立递推关系式
2.3神经网络中经常用到的Σ符号
1.Σ符号的含义
表示数列的总和
2.Σ符号的性质
线性性质:
1.和的Σ为Σ的和;
2.常数倍的Σ为Σ的常数倍;
2.4有助于神经网络的向量基础
1.有向线段
(起点)A---->B(终点)
2.向量
(1)向量是具有方向和大小的量;
(2)向量的坐标表示:把箭头的起点放在原点,用箭头的终点的坐标表示向量,向量a = (a1,a2);
(3)向量的大小:表示向量的箭头的长度称为这个向量的大小,用|a|表示,|a| = √(a1^2 + a2^2);
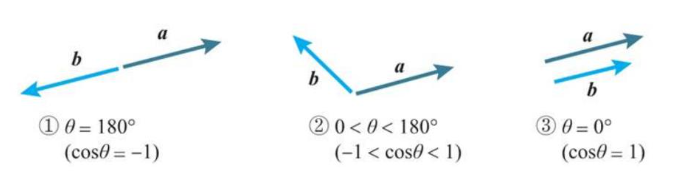
(4)向量的内积:a · b = |a|*|b|*cos(θ),(θ为a,b夹角);
3.柯西-施瓦茨不等式
-|a||b| <= a · b <= |a||b|
梯度下降法的原理:
(1)当两个向量方向相反时,内积取得最小值;
(2)当两个向量不平行时,内积取平行时的中间值;
(3)当两个向量方向相同时,内积取得最大值;
通过内积可以知道两个向量的相对的相似度;
4,内积的坐标表示
当向量a(a1,a2) , b(b1,b2)时,a · b = a1a2 + b1b2;
当向量a(a1,a2,a3) , b(b1,b2,b3)时,a · b = a1a2 + b1b2 + a3b3;
5.向量的一般化
(1)向量的坐标表示:a = (a1,a2,…,an)
(2)内积的坐标表示:a · b =(a1b1,a2b2,…,anbn)
(3)柯西-施瓦茨不等式:-|a||b| <= a · b <= |a|*|b|
6.加权输入表示为内积形式
神经单元有多个输入x1,x2,…,xn时,将它们整理为如下加权输入,z = w1x2,w2x3,…,wnxn + b;
其中w1,w2…wn为权重,b为偏置,;
使 w =(w1,w2…wn),x =(x1,x2…xn)这两个向量,我们可以将加权输入表示为内积形式,z = w·x + b
2.5有助于神经网络的矩阵基础
1.矩阵的定义
(1)矩阵是数的阵列,横排是行,竖排是列,位于第 i 行第 j 列的值(称为元素)用aij 表示;
(2)方阵:行数和列数相同的矩阵;
(3)行向量、列向量
(4)单位矩阵:对角线上的元素 aii 为1,其他元素为 0 的矩阵;
2.矩阵相等
两个矩阵A、B相等的含义是它们的元素对应相等,记A = B;
3.矩阵的和、差、常数倍
(1)两个矩阵A、B的和A+B,差A-B定义为相同位置的元素的和、差所产生的矩阵;
(2)矩阵的常数倍定义为各个元素的常数倍所产生的矩阵;
4.矩阵的乘积
(1)对于两个矩阵 A、B,将 A 的第 i 行看作行向量, B 的第 j 列看作列向量,将它们的内积作为第 i 行第 j 列元素,由此而产生的矩阵就是矩阵;
(2)矩阵的乘法不满足交换律:AB !=BA
(3)单位矩阵与任意矩阵的乘积满足以下交换律:AE = EA =A
5.转置矩阵
将矩阵 A 的第 i 行第 j 列的元素与第 j 行第 i 列的元素交换,由此产生的矩阵称为矩阵 A 的转置矩阵,用 tA、At 等表示
2.6神经网络的导数基础
1.导数的定义

(1)已知函数 f(x),求导函数 f’(x),称为对函数 f(x) 求导
(2)当导函数的值存在时,称函数可导
(3)神经网络中用到的函数的导数公式:
2.导函数的含义

3.导数符号
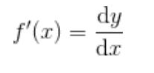
4.导数的性质
线性性
5.最小值的条件

2.7神经网络的偏导数基础
1.多变量函数的定义
有两个以上自变量的函数称为多变量函数;
2.偏导数
关于某个特定变量的导数称为偏导数
3.多变量函数的最小值条件

三、神经网络的数学基础(下)
3.1误差反向传播法必需的链式法则
1.神经网络和复合函数
已知函数 y = f(u),当 u 表示 u = g(x)时,y 作为 x 的函数可以表示为形如 y = f(g(x))的嵌套结构(u,x表示多变量),这时,嵌套结构 f(g(x))称为发 f(u)和 g(x)的复合函数;
2.单变量函数的链式法则
已知单变量函数 y = f(u),当 u 表示为单变量函数 u = g(x)时,复合函数 f(g(x))的导函数可以如下求出:
3.多变量函数的链式法则