二项分布_二项分布的分布律

       

   说起二项分布(binomial distribution)，不得不提的前提是伯努利试验(Bernoulli experiment)，也即n次独立重复试验。伯努利试验是在同样的条件下重复、相互独立进行的一种随机试验。

   伯努利试验的特点是：

（1）每次试验中事件只有两种结果：事件发生或者不发生，如硬币正面或反面，患病或没患病；

（2）每次试验中事件发生的概率是相同的，注意不一定是0.5；

（3）n次试验的事件相互之间独立。

   举个实例，最简单的抛硬币试验就是伯努利试验，在一次试验中硬币要么正面朝上，要么反面朝上，每次正面朝上的概率都一样p=0.5，且每次抛硬币的事件相互独立，即每次正面朝上的概率不受其他试验的影响。如果独立重复抛n=10次硬币，正面朝上的次数k可能为0,1,2,3,4,5,6,7,8,9,10中的任何一个，那么k显然是一个随机变量，这里就称随机变量k服从二项分布。

 

   

   我们推导下随机变量X=k的分布律。显然0<=k<=n，n次抛硬币中获得k次正面，第1次正面在n次抛硬币中出现有n种方式，则第2次正面在n次抛硬币中出现有n-1种方式，以此类推，则出现的总可能方式是：n(n-1)...(n-k+1)种，如果我们并不考虑这k次正面出现的排列顺序，因此恰好出现k次的总可能性是n(n-1)...(n-k+1)/k！种，分子和分母同时乘以(n-k)！，则该式等于n！/(k！*(n-k)！)，也就是通常的组合公式C(n,k)=n！/(k！*(n-k)！)。

        那么对于抛n次硬币，其中正面出现的次数是k，反面出现的次数必然为n-k次，不考虑顺序的情况下，则每一次恰好获得k次正面的概率是p^k*(1-p)^n-k，而n次试验中恰好出现k次正面的可能性是C(n,k)=n！/(k！*(n-k)！)种，因此，n次抛硬币中恰好出现k次的概率为

P(X=k) = C(n,k) * p^k*(1-p)^n-k

这就是二项分布的分布律，记作X~B(n,p)，其中C(n,k)是组合数，在数学中也叫二项式系数，这就是二项分布名称的来历。判断某个随机变量X是否符合二项分布除了满足上述的伯努利试验外，关键是这个X是否表示事件发生的次数。二项分布的数学期望E(X)=n*p，方差D(X)=n*p*(1-p)，具体证明可见《二项分布均值和方差的简单推导》。

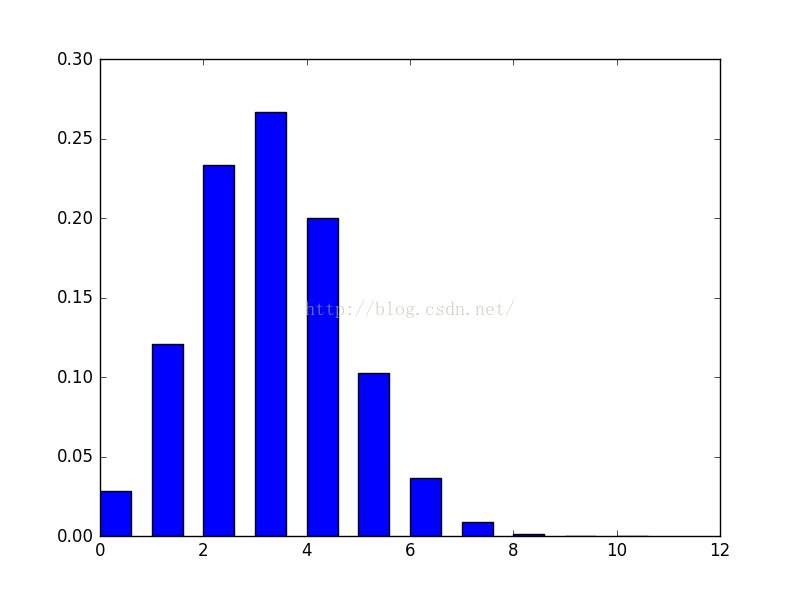
   看一个示例：某人篮球投篮的命中率是0.3，总共投篮10次，问至少投中2次的概率?

分析：

（1）每次投篮有2种结果，投中或没投中；

（2）每次投篮的投中概率是相同的，都为0.3；

（3）每次投篮可认为是独立事件。

 因此，符合二项分布。

投中次数的概率质量分布

   显然，二项分布属于离散型分布。

   至少2次投中概率即：P(X>=2)=P(X=2)+P(X=3)+P(X=4)+...+P(X=10)。

import numpy as np
import scipy.stats as sps
n = 10
p = 0.3
k = np.arange(n + 1)
PX = sps.binom.pmf(k, n, p)
print(sum(PX[2:]))

输出结果：

0.85

   再看一个例子：某种疫苗注射后过敏反应的概率是0.08，问某社区卫生院在接种该疫苗100人后，少于3人有过敏反应的概率是多少？

采用上例中的分析方法，该问题也属于二项分布问题。少于3人有过敏反应，即求：

P(X<3)=P(X=0)+P(X=1)+P(X=2)=C(100,0)(0.08)⁰(0.02)¹⁰⁰+C(100,1)(0.08)¹(0.02)⁹⁹+C(100,2)(0.08)²(0.02)⁹⁸=0.01127=1.127%

   在实际应用中还有伯努利分布、两点分布、0-1分布等，它们与二项分布之间有什么关系呢？

         X~B(n,p)，当n = 1时，二项分布就变成了伯努利分布(Bernoulli distribution)，伯努利分布又称为“两点分布”或“0-1分布”，或者说伯努利分布/两点分布/0-1分布是二项分布在n=1时的特例，即伯努利分布、两点分布、0-1分布这三种分布是同一个分布的不同名称，又都是二项分布在n=1时的特例。