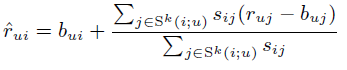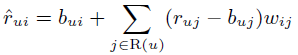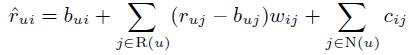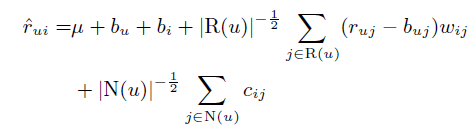- 1【正点原子FPGA连载】第一章Hello World实验 摘自【正点原子】DFZU2EG_4EV MPSoC之嵌入式Vitis开发指南_xczu4ev-sfvc784-1-i 原理图
- 2PgSQL过程中遇到的查询效率过慢问题
- 3[Python进阶] WindowsAPI:pywin32_python win32api
- 4基于java springboot仓库管理微信小程序源码_java+ 微信小程序物资管理系统
- 5canvas导出图片python_Python连连看小游戏源代码
- 6Unity手机游戏开发:从搭建到发布上线全流程实战
- 7School StartsFirstProject~UnityVR(HTCVive设备开发)_htc vive unity开发
- 8如何在Pycharm中导入第三方库(以pyecharts为例子)
- 9图解云原生应用设计模式_云原生应用 开发模式
- 10linux ACL权限,设定,删除_/dev/shm添加acl权限
结合因式分解(SVD++)与近邻模型的混合协同过滤推荐系统_基于svd++和ubcf算法的混合推荐方法
赞
踩
一、 介绍
推荐系统现在的应用已经非常广泛了,协同过滤(CF)是一种常见的推荐系统,仅根据用户过去的行为来进行推荐,不需要domain knowledge,也不需要进行大规模的数据收集。CF又分为 Neighborhood model (比如User-based 和 Item-based) 和 Latent factor model (例如SVD)。Neighborhood models 可以发现局部的强关联,但是不能发现全局性的特征和关联(因为其本质上是KNN), Latent factor model 可以挖掘全局性特征,却不能发现局部强关联。因此本文介绍的混合推荐系统将这两种模型结合起来,以期待既挖掘出局部强特征,又保留全局性特征。CF 算法的 Baseline estimates 是
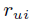
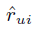
二、 Neighborhood models
对物品相似度的计算有各种不同的方法,jaccard、cosin similarity等,SVD++ 论文中所采用的方法是
在 baseline 的基础上增加了对被预测物品的各相似物品的误差的拟合,各相似物品的误差权重即为两者相似度,并对误差之和归一化。
其中 Sk 意为与物品 i 较像的 k 个物品的集合。
该模型具有可解释性、易实现等优势,缺点是如果用户 u 没有对物品 i 的相似物品打过分,预测得分就会变成 baseline, 而且只考虑 i 的相似物品集,未考虑全局特征。
三、 Latent factor models
这个类型的模型有很多,在这里我们使用 SVD 模型。SVD 模型的预测公式为: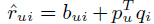
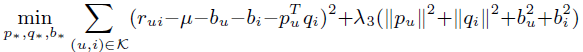
四、 隐式反馈
打分是用户对数据集的显式反馈,还有一些隐式反馈,如点击而未打分等。 SVD++ 综合利用了显式反馈和隐式反馈,使用更多的反馈数据可以提高模型的准确度。
五、 新 Neighborhood model
在增加隐式反馈的基础上,我们改进一下上面的Neighborhood model, 第一步将预测公式改进为
这里有两个较大的改动,一个是用 wij 代替 sij,之前的 sij 是基于皮尔逊系数的物品之间的相似度,这里的 wij 则是通过学习来得到的权重系数,不止局限于有共同打分记录的物品间,而是全局每两个物品之间都会有一个权重系数,并且未对 wij 进行归一化操作。这样,当两个物品的关联系数较小时,哪怕物品 j 的 baseline 拟合误差很大,对物品 i 的影响也很小。而当两个物品的关联系数很大时,哪怕物品 j 的baseline拟合误差很小,也会对 i 产生较大影响。
第二步的改动是
与第一步的区别是加了 cij, cij 是另一组需要学习的权重系数,和 wij区别在于来自的集合不同。 wij 中的物品 j 来自于显式反馈集合 R ,即物品 i j 被共同打过分; 而 cij 中的物品 j 来自于隐式反馈集合 N ,即物品 i j 可能没被打过分,但被同一用户点击过。
我们可以看到,在上面的公式中,有较多打分行为或隐式行为的用户会更多地偏离 baseline estimates,有较少行为的用户则会更接近于 baseline 的预测。而这有些过于强调了两类用户的不同,因此,第三步改进如下,加入了对行为次数的约束。
为了减少模型复杂度,可以做进一步改进,公式如下。新公式的集合上方有 k 意味着只考虑与物品 i 最接近的 k 个物品。当k取向于无穷大时,此公式趋向于上一公式。这样可以大大减少要学习的系数。
相应的损失函数如下:
其对应的系数更新公式如下
六、 Asymmetric-SVD 与 SVD++
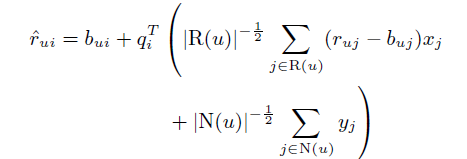
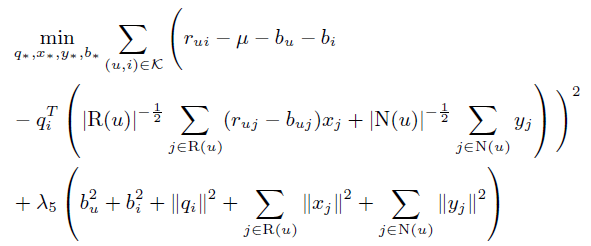
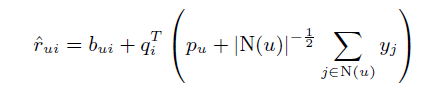
七、 混合模型

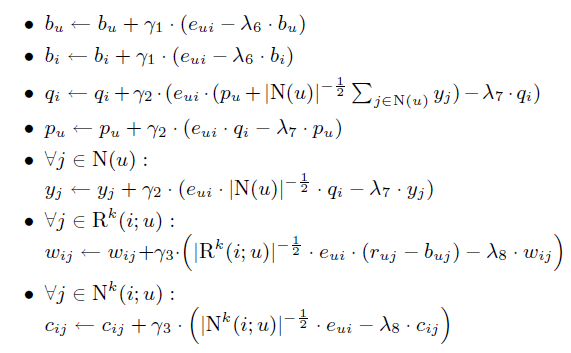
Copyright © 2003-2013 www.wpsshop.cn 版权所有,并保留所有权利。