- 1斯坦福CS193U-虚幻4C++课程学习笔记(14)_虚幻4 bindufunction
- 2STM32 HAL库开发——入门篇(2):定时器_stm32 hal 定时器
- 3分类问题的评价指标:多标签分类【基于标签度量(同多分类一样):准确率(Accuracy)、精确率(Precision)、召回率(Recall)、F1】【基于样本度量:Hamming Loss...】_多分类和多标签共用的评价指标
- 4TensorRT 安装笔记_the package you are trying to install is only a pl
- 5MongoDB的介绍和使用
- 6Vue视频插件(vue-video-player)_vue video player
- 7Ubuntu释放缓存/内存和显存_ubuntu 释放内存
- 8【RN】为项目使用React Navigation中的navigator
- 9小鹤双拼记忆口诀_你必须要掌握的一个小技能——双拼输入
- 10神经网络量化原理
MATLAB环境下基于变分贝叶斯的组织学病理图像颜色盲反卷积方法
赞
踩
图像盲反卷积问题仅根据模糊图像估计清晰图像和模糊核,也是一个欠定问题且求解更加困难。但图像盲反卷积算法更实际,因为许多情况下,模糊核都是未知或部分已知的。求解盲反卷积问题需要为未知量选择适当的先验模型,以得到清晰图像和模糊核的确定解。
贝叶斯推理的变分技术的发展遵循两条平行但独立的轨道。早在1987年,Peterson等研究了特定模型的第一个变分过程:神经网络。这篇论文以及统计力学的见解导致了一系列各种各样模型的变分推理程序。1993年,Hinton等为神经网络模型提出了一种变分算法。Dempster等提出变分贝叶斯推断算法与期望最大化算法建立重要的联系,然后导致了针对其他类型模型的多种变分推理算法的出现。
近年来变分贝叶斯推断算法成为了研究者们研究的热点,该算法被广泛用于模型参数的估计以及对模型的选择。目前,变分贝叶斯推断算法在大多数领域的应用有很多研究,例如将该算法应用信息科技、医学等领域。现代变分贝叶斯推理研究主要集中在几个方面:(1)处理涉及海量数据的贝叶斯推理问题;(2)使用改进的优化方法来求解方程最优变分后验分布;(3)开发通用变分贝叶斯推理,将该算法易于应用于各种模型,并提高变分推理的准确性。
鉴于图像盲反卷积和变分贝叶斯方法的优势,提出一种基于变分贝叶斯的组织学病理图像颜色盲反卷积方法,算法运行环境为MATLAB R2018A,压缩包=数据+代码+参考文献。部分代码如下:
- %% Load image and reference vectors
- clc,clear all
- I = imread('histWB.jpg');
- load 'MLandini' RM;
- [m,n,nc] = size(I);
- subplot(241),imshow(I)
- title('Original H&E Image')
- %% Deconvolution
- ns=2; %number of stains
-
- epsilon = 2.0e-5;
- niter = 1000;
-
- %% Band visualization (OD space)
-
- ns = size(M,2)
- concentrations = reshape(CT',m,n,ns);
- %figure()
- subplot(242),imshow(concentrations(:,:,1))
- title('OD H Band')
- subplot(246),imshow(concentrations(:,:,2))
- title('OD E Band')
- %% Band reconstruction (RGB space)
- Hrec_OD = reshape((M(:,1)*CT(1,:))',m,n,nc);
- Hrec_RGB = OD2intensities(Hrec_OD);

出图如下:
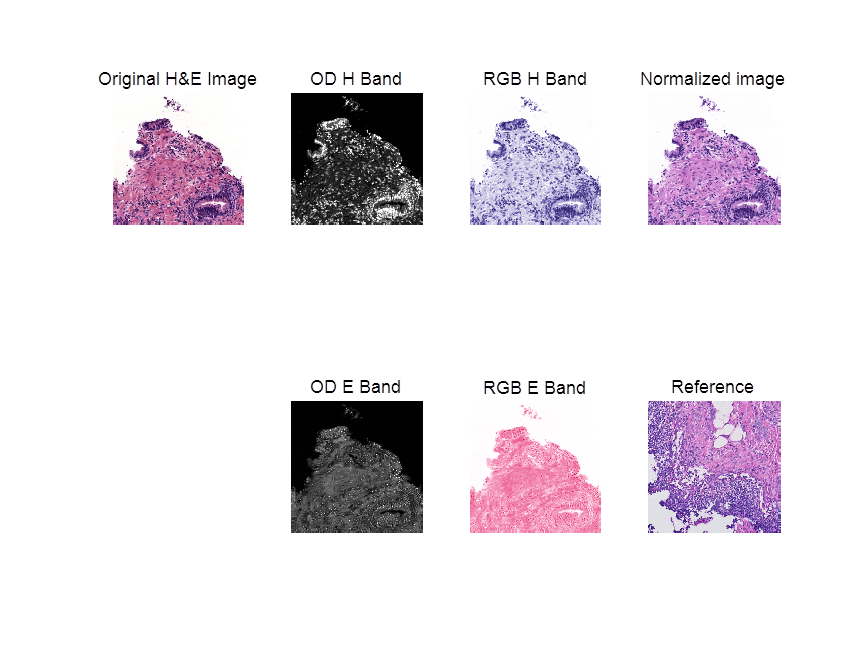
工学博士,担任《Mechanical System and Signal Processing》审稿专家,担任
《中国电机工程学报》优秀审稿专家,《控制与决策》,《系统工程与电子技术》,《电力系统保护与控制》,《宇航学报》等EI期刊审稿专家。
擅长领域:现代信号处理,机器学习,深度学习,数字孪生,时间序列分析,设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。


