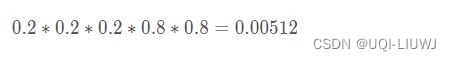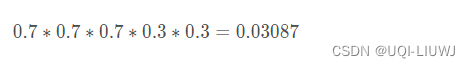- 1jenkins自动化部署_jenkins打包,发布,部署
- 2vuecli3直接在本地打开dist文件中的index.html出现白屏的问题_vue dist 不能直接访问
- 3自然语言处理实验—用隐马尔可夫模型在分词中的应用计算概率矩阵(含python代码和详细例子解释)_发射概率矩阵
- 4【Kotlin基础系列】第6章 包与导入_kotlin import
- 5华为系统鸿蒙流畅度,鸿蒙系统流畅度怎么样 华为鸿蒙系统流畅度评测详解
- 6微信小程序--Taro框架实际开发中的问题汇总_taro 小程序 报错 exports.usecontext (vendors.js? [sm]:1
- 7python学生管理器_完成数据模型类studentmodel
- 8当微信小程序邂逅知识问答,订单就按耐不住了!_mini订单内容
- 9从关键新闻和最新技术看AI行业发展(2023.12.4-12.17第十二期) |【WeThinkIn老实人报】_phi-2 开源地址
- 10鸿蒙OS基于安卓11,华为鸿蒙OS 2.0、EMUI 11对比:安卓底层没了
机器学习笔记:EM算法(期望最大算法)_期望最高求法
赞
踩
1 算法介绍
1.0 EM算法的引入
EM算法主要解决的问题是,具有隐变量的混合模型的参数估计,即其极大似然估计
如果是简单的问题,我们可以直接求出P(x|θ)的时候,我们可以直接用最大似然估计来求出解析解
但如果在模型中有了隐变量之后,就不太好求解析解P(x|θ)了,也就无法用最大似然估计来得到最佳的θ
——》这时候就需要EM算法了
1.1 EM算法介绍
EM算法是一个迭代的算法,其会不断地更新θ,直至收敛。
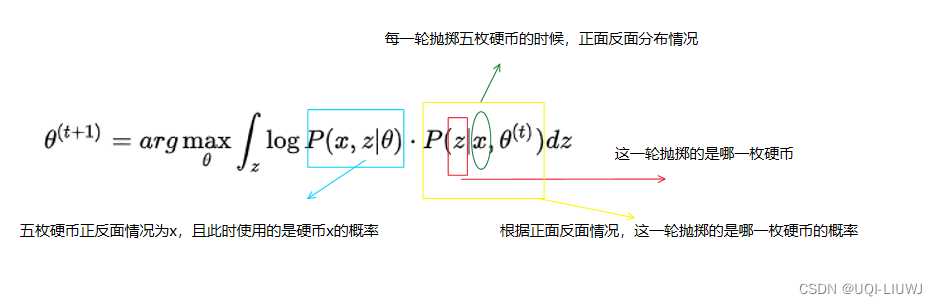
第t轮迭代的公式如下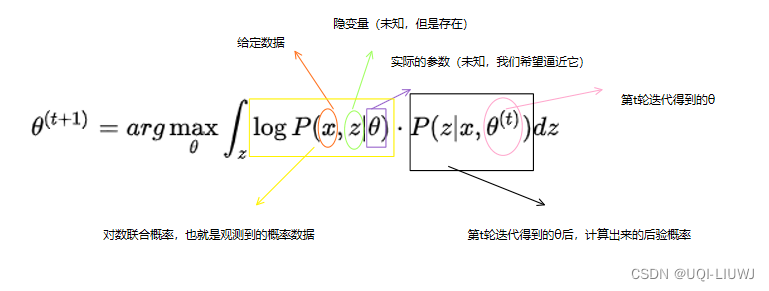
我们对上式稍作修改,便有了期望形式:
——>EM 算法可以分成两步
————>第一步(E):求出期望
————>第二步(M):期望最大化
2 EM算法推导
2.1 第一种推导方法:ELBO+KL散度
根据条件概率的性质,我们有:
进一步化简
令q是任意一个关于z的分布:
也就是
对等号两边求期望,有:
左边
右边
- KL散度见NTU 课程 CE7454:信息论概述_UQI-LIUWJ的博客-CSDN博客
- ELBO表示evidence lower bound
因为KL散度始终大于等于0(当KL散度比较的两个分布相同时取等号),所以
,当q(z)和
分布相同时取等号。
于是我们令q(z)就是
所以
由于
和θ无关,所以
不难发现和第一小节的式子是一样的

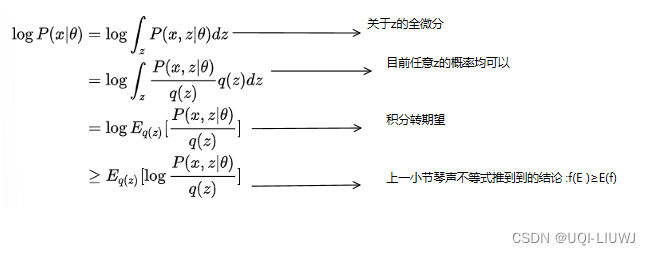
2.2 第二种推导方法:ELBO+琴声不等式
2.2.1 琴声不等式
对于凸函数f,f[ta+(1-t)b]≥tf(a)+(1-t)f(b)
等号成立条件 a=b
在这里,我们令t为0.5:
也即f(E)≥E(f)
2,2,2 推导
这里等号成立条件,对所有的z,
均相等,我们令其为C
不难发现
就是2.1中说的ELBO,下面的问题就在于,q(z)此时是否等于
——>
等号两边对z求微分

【最后一个等号:关于z的全微分,所以把z可以提出来】
所以
,将其带入
所以用这种方式也能推导出EM的式子
3 EM算法举例:抛硬币问题
3.0 问题的引入:没有隐变量z的情况
假设现在有两枚硬币1和2,,随机抛掷后正面朝上概率分别为P1和P2。
为了估计P1和P2,每次取一枚硬币,连掷5下,记录的结果如下所示:
| 硬币 | 结果 | 统计 |
|---|---|---|
| 1 | 正正反正反 | 3正-2反 |
| 2 | 反反正正反 | 2正-3反 |
| 1 | 正反反反反 | 1正-4反 |
| 2 | 正反反正正 | 3正-2反 |
| 1 | 反正正反反 | 2正-3反 |
在这种情况下,由于我们知道每一次抛掷的是哪一枚硬币,所以概率很好求
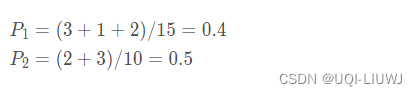
3.1 引入隐变量z
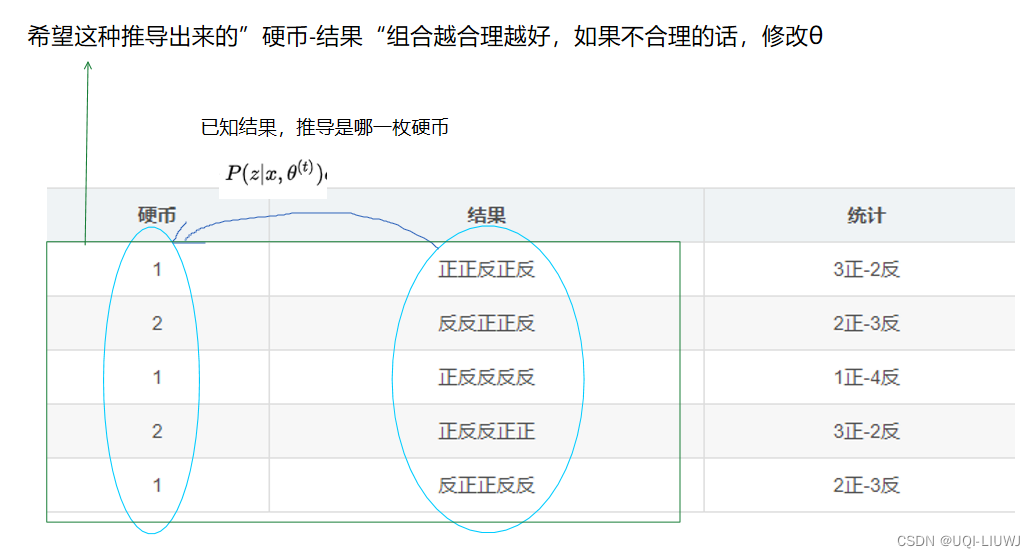
现在我们不知道每轮投掷时使用的是哪一每硬币,那么此时记录的结果如下所示:
硬币 结果 统计 Unknown 正正反正反 3正-2反 Unknown 反反正正反 2正-3反 Unknown 正反反反反 1正-4反 Unknown 正反反正正 3正-2反 Unknown 反正正反反 2正-3反 那么现在怎么估计P1和P2呢?
这时候就需要EM算法了
用期望的形式写,翻译成白话就是:假定我们知道了 硬币朝向和抛掷硬币的对应关系,那么我们希望此时 出现的各种 (硬币朝向,抛掷硬币)对的概率最大
3.2 解决方法
我们先 随便给P1和P2赋一个值,比如P1=0.2,P2=0.7
第一轮是:正正反正反,那么是硬币1/硬币2的概率为
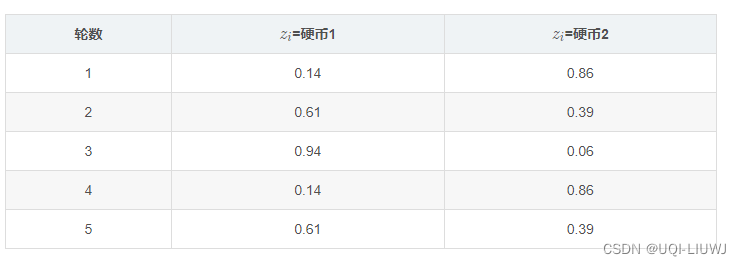
于是我们可以得到这五轮的概率
然后我们对每一行,分别计算是硬币1 or 硬币2的概率
接下来,我们需要重新估计P1和P2(θ)
计算一下期望,看看有多少次等价的硬币1抛出来为正,多少次抛出来为负
以硬币1为例,其第一轮的正正反正反,等价于 一枚硬币1期望跑出如下的正负次数

同理可得硬币1其他轮次的情况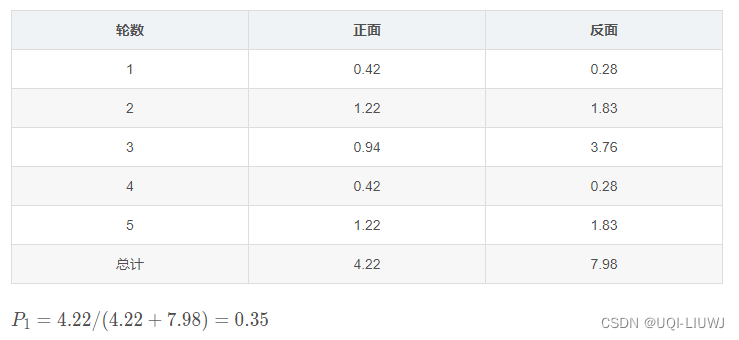
4 K-means
 K-means是一个clustering的模型,首先我随机挑几个点作为center(center是哪几个点就是这边的隐变量),然后每一轮我根据点和cluster 中心点的远近程度,重新找cluster中心点
K-means是一个clustering的模型,首先我随机挑几个点作为center(center是哪几个点就是这边的隐变量),然后每一轮我根据点和cluster 中心点的远近程度,重新找cluster中心点
参考内容