- 1SpringBoot3.0 集成 Redis2.6_springboot3.0 redis
- 2决胜B端(二)设计篇-从业务诊断到形成方案-调研_决胜b端2
- 3github上如何添加Demo动画_github.io在个人主页添加视频
- 4JAVA安全之Log4j-Jndi注入原理以及利用方式
- 5DataGridView取消默认选中行_datagridview取消选中状态
- 6MySQL的安装与环境变量配置_mysql中如何设置环境变量
- 7学校作业5_3字符串_统计英文文件中的单词数(头哥作业[Python])_统计英文文件中的单词数python头歌
- 8微信小程序picker多列选择器:四级联动
- 9ant design pro v5 - 03 动态菜单 动态路由(配置路由 动态登录路由 登录菜单)_ant design pro 动态菜单
- 10垃圾分类数据集-8w张图片245个类附赠tensorflow代码_垃圾分类数据集(垃圾图片数据集)
人工智能入门
赞
踩
一、人工智能入门
人工智能(Artificial Intelligence),英文缩写为AI。它是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学。
人工智能是计算机科学的一个分支,它企图了解智能的实质,并生产出一种新的能以人类智能相似的方式做出反应的智能机器,该领域包括机器人、语言识别、图像识别、自然语言处理和专家系统等。人工智能可以对人的意识、思维的信息过程进行模拟。
思想阶段
人工智能的最初思想是创造像人一样有自我意识和思维能力的生命体。这种思想萌芽于古希腊时代,希腊神话中的塔洛斯和潘多拉都是这种思想的体现。
近代主要以阿西莫夫等科幻小说作家为代表,提出了著名的“机器人三大定律”。
思想阶段的产物
第一定律:机器人不得伤害人类个体,或者目睹人类个体将遭受危险而袖手不管。
第二定律:机器人必须服从人给予它的命令,当该命令与第一定律冲突时例外。
第三定律:机器人在不违反第一、第二定律的情况下要尽可能保护自己的生存。
科学阶段
基于规则的系统。将关于世界的知识用形式化的语言进行硬编码,计算机使用逻辑推理规则来自动理解这些形式化语言中的声明。计算机并没有获得自我学习的能力。
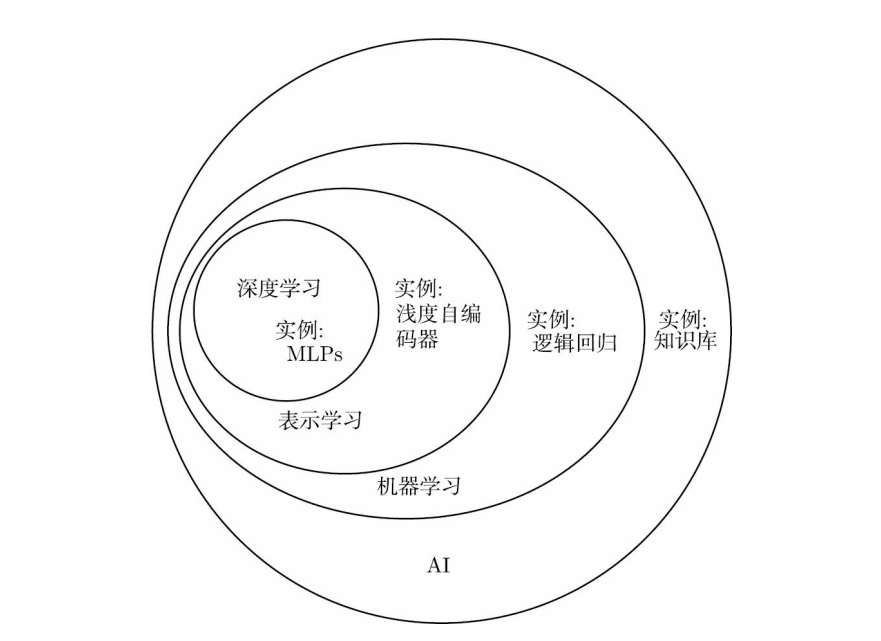
机器学习。赋予计算机从特征集中提取模式的能力。人为设置一个特征集,计算机经过训练可以学习这些特征跟最终的结果如何关联。机器学习的性能很大程度上依赖于给定数据的表示。
表示学习。使用机器学习方法来发掘数据的表示本身,而不是仅仅把人类提炼好的特征映射到结果。也就是让计算机自己去发掘特征集。但是从原始数据中提取高层次抽象的特征是非常困难的。
深度学习。通过比较简单的表示来表达复杂表示,解决了表示学习中的核心问题。例如在图像识别中,深度学习通过像素这种最初级的表示去提取边,通过边去提取角度和轮廓,通过角和轮廓去提取对象,最终映射到输出结果。


二、数学建模入门
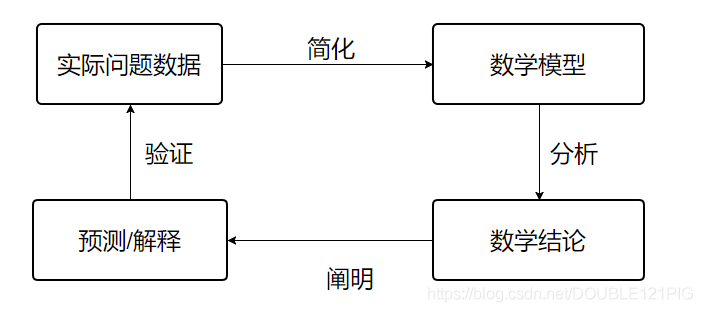
数学建模(Mathematical Modeling),它是利用数学方法解决实际问题的一种实践。即通过抽象,简化,假设,引进变量等处理过程,将实际问题用数学方式表达,建立起数学模型。
数学建模是对现实世界的理想化,但永远不会是完全精确的表示,尽管任何模型都有其局限性,但是好的模型能够提供有价值的结果和结论。
伽利略发现自由落体的数学规律。他的原话是:“奇数1,3,5,7隐藏在物体的下落过程中。”
设下落时间为t。
自由落体的下落距离s=1/2*(g*t的平方)。
第1秒的下落距离s1=1/2*g=1/2*g*1;
第2秒的下落距离s2=1/2*g*(4-1) =1/2*g*3;
第3秒的下落距离s3=1/2*g*(9-4) =1/2*g*5;
第4秒的下落距离s4=1/2*g*(16-9) =1/2*g*7;
伽利略发现自由落体的数学规律的过程也是一个数学建模的过程。他面临的最大难点在于对准确数据的收集,最大亮点是对简化原则的使用。
伽利略的建模过程
在伽利略的年代(16世纪),如何准确记录落体的下落时间和下落距离?
没有精确的计时器,也没有摄像机。
伽利略想到一个绝妙的解决办法,那就是减缓运动速度。他让一个小球缓慢的滚下斜坡(在物理学中被称为斜面)。
伽利略用一块长而薄的木板作为斜面,沿纵向切出一个凹槽作为小球的通道。通过减缓斜面的斜率直到接近水平状态,他可以使球的下降速度变得尽可能缓慢,即使运用那时可用的仪器,也能测量出球在每一刻的位置。
伽利略利用水钟作为计时工具。开始计时的时候,打开阀门,水会以恒定的速度通过细管流入容器。停止计时的时候,关闭阀门。通过对球下降过程中容器里积累的水进行称重,他可以将流逝的时间精确到比较理想的程度。
伽利略说他把“凹槽雕刻得非常平直,打磨地十分光滑”。他为什么要这么做?他要避免什么?
面对复杂的数学建模问题,伽利略做出了正确的选择 :简单,简洁和最小化。
输入都是海量的原始数据。
都依赖数学知识,如微积分,线性代数,概率论,统计学等。
都要针对问题建立相应的数学或算法模型。
得到的结论都需要在实践中进行验证。
根据验证的结果不断优化模型。
结论:人工智能和数学建模有着高度一致的方法论。人工智能离不开数学建模的思想方法,从数学建模的角度去理解和学习人工智能是一种合适的学习方法。
三、数学基础
统计量(数理统计)
矩阵概念和计算(线性代数)
概率和概率分布(概率论)
导数,微分,积分(高等数学)
总体(全部研究对象,如全校学生的身高)
个体(总体的一个基本单位,如学生A的身高x=170)
样本(若干个体的集合,是总体的一部分)。样本的数理成为样本容量。
统计的任务就是从样本去推测总体。
算术平均值(均值)

中位数(将数据从小到大排序后位于中间位置的那个数值)
标准差

方差(标准差的平方)
极差是样本中最大值与最小值的差
矩阵是对类似产量统计表,价目表等数理关系的表示
例如,某户居民第二季度每个月的水,电,天然气的使用情况

矩阵有m行,n列,则称为m×n矩阵。
记作
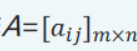
当m=n时,称为n阶矩阵或n阶方阵。
零矩阵 矩阵中所有元素都是0
单位矩阵 必然是方阵,对角线上元素全是1,其余元素全是0。
矩阵相等 两个矩阵A和B的行数和列数都相同,且每两个相同位置上的元素都相等。
记作
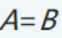
加法 两个m×n矩阵相加,则每两个相同位置上的元素做加法。
记作

同理,两个矩阵的减法记作
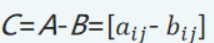
数乘 λ为任意实数,矩阵C是λ与矩阵A的乘积,则矩阵C的每个元素等于矩阵A的对应位置元素乘以λ 。记作

乘积 A是m×s矩阵,B 是s×n矩阵,则矩阵C为A和B的乘积,其中C的元素aij等于A的第i行元素与B的第j列对应元素的乘积之和。记作

互斥事件与对立事件
事件A和B不可能同时发生,则A和B为互斥事件。
记作P(A∪B)=P(A)+P(B)
其中必有一个发生的互斥事件叫做对立事件。
记作P(A)=1-P(B)
独立事件与对立事件
事件A或B发生时,事件B或A的发生概率不受影响,则A和B为独立事件。
记作P(AB)=P(A)P(B)
伯努利分布
是只有两种可能结果的单次试验,例如扔一次硬币的概率分布。
二项分布
是n重伯努利分布,在同一条件下重复n次独立的试验。单次实验中A发生的概率为p,A出现的次数k是一个随机变量

多项式分布
将二项展开为多项就得到多项分布,例如掷色子。

高斯分布
正态分布,是一种连续的分布,有着很广泛的应用,例如本市同年龄的男生或女生身高。



