[论文笔记]Root Mean Square Layer Normalization

引言

今天带来论文Root Mean Square Layer Normalization的笔记，论文题目是均方根层归一化。

本篇工作提出了RMSNorm，认为可以省略重新居中步骤。

简介

层归一化对Transformer等模型非常重要，它可以帮助稳定训练并提升模型收敛性，因为它能够处理输入和权重矩阵的重新居中(re-centering)和重新缩放(re-scaling)。然而，LayerNorm引入的计算开销使这些改进变得昂贵，并且严重减慢了底层网络的速度。

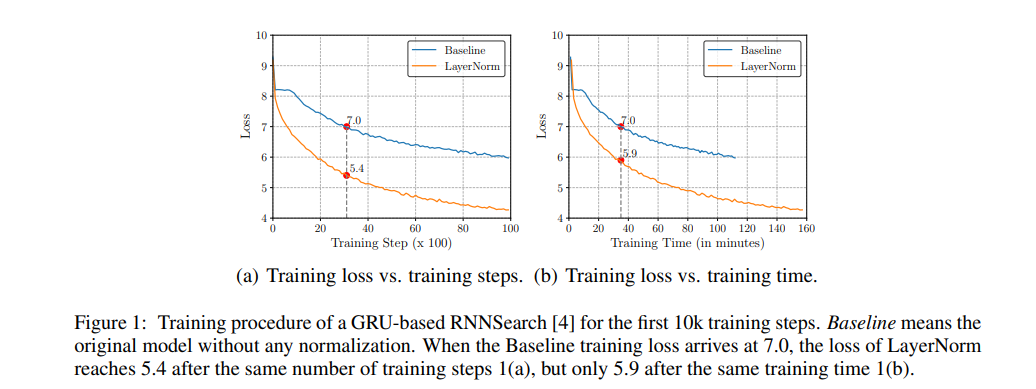
对于少量归一化层的小型和浅层神经模型来说，这个问题是微不足道的。但当底层网络变得更大更深时，这个问题就变得严重了。

因此，从更快、更稳定的训练(以训练步骤的数量为衡量)中获得的效率提升被每个训练步骤增加的计算成本所抵消，这降低了净效率，如图1所示。

在本篇工作中，作者提出了均方根层归一化(MSNorm)，它仅使用均方根统计数据对一层中神经元的总输入进行正则化。与LayerNorm相比，RMSNorm减少了计算量，提高了效率。尽管公式更简单，但RMS归一化器有助于稳定层激活的幅度，确保对权重和数据集的重新缩放具有不变性。

背景知识

本节简要回顾了基于标准前馈神经网络的LayerNorm。给定一个输入向量 $x\text{x}x\in {\mathbb{R}}^m$，一个前馈网络通过线性变换将其投影到一个输出向量 $y\text{y}y\in {\mathbb{R}}^n$​，然后通过非线性激活进行如下处理：
$$a_i=\sum _{j=1}^m{w}_{ij}{x}_j,y_i=f(a_i+b_i)\text{\hspace{1em}(1)}$$
其中$w_i$是第 i 个输出神经元的权重向量，$b_i$是通常初始化为0的偏置标量，$f(\cdot )$是逐元素的非线性函数。$\pmb a ∈ \R^n $​表示神经元的加权和输入，也是归一化的目标。

这个普通的网络可能会遭受内部协变量偏移问题，即随着前面的层被更新，某一层的输入分布也会发生变化。这可能会对参数的梯度稳定性产生负面影响，延迟模型的收敛。为了减少这种偏移，LayerNorm 对输入进行归一化，使其均值和方差保持不变，具体如下：
$${\bar{a}}_i=\frac{a_i-\mu }{\sigma }{g}_i,y_i=f({\bar{a}}_i+b_i)\text{\hspace{1em}(2)}$$

其中${\bar{a}}_i$是向量$\overline{a\text{a}a}\in {\mathbb{R}}^n$的第 i 个值，它作为$a_i$在层激活中的归一化替代值。$g\text{g}g\in {\mathbb{R}}^n$ 是用于重新缩放标准化的加权和输入的增益参数，初始值设为1。$\mu$和${\sigma }^2$分别是从原始加权和输入$a\text{a}a$估计得出的均值和方差统计量：
$$\mu =\frac{1}{n}\sum _{i=1}^n{a}_i,\sigma =\sqrt{\frac{1}{n}\sum _{i=1}^n(a_i-\mu {)}^2}\text{\hspace{1em}(3)}$$

RMSNorm

LayerNorm成功的一个著名解释是其重新居中和重新缩放不变性属性。前者使得模型对于输入和权重上的偏移噪声不敏感，而后者在输入和权重都被随机缩放时保持输出表示不变。在本文中，作者假设重新缩放不变性是LayerNorm成功的原因，而不是重新居中不变性。

作者提出了RMSNorm，它仅关注重新缩放不变性，并根据均方根统计量简单地对加权和输入进行正则化：
$${\bar{a}}_i=\frac{a_i}{\text{RMS}(a\text{a}a)}{g}_i\text{\hspace{1em}(4)}$$
其中$\text{RMS}(a\text{a}a)$为：
$$\text{RMS}(a\text{a}a)=\sqrt{\frac{1}{n}\sum _{i=1}^n{a}_i^2}\text{\hspace{1em}(4.1)}$$
对比公式(4)和(2)发现，确实只是去掉了均值$\mu$。RMSNorm通过完全删除公式(3)中的均值统计量简化了LayerNorm。当加权和输入的均值为零时，RMSNorm与LayerNorm完全相等。虽然RMSNorm不像LayerNorm那样重新居中加权和输入，但通过实验证明，这个属性并不是LayerNorm成功的根本原因，而且RMSNorm同样或更加有效。

RMS测量输入的平方均值，在RMSNorm中，它将加权和输入强制缩放到一个$\sqrt{n}$倍的单位球中。通过这样做，输出分布不受输入和权重分布的缩放影响，有利于层激活的稳定性。虽然欧几里得范数与RMS仅差一个$\sqrt{n}$的因子，已经成功应用于一些领域，但经验证明，它在层归一化中并不奏效。

作者假设根据输入向量的大小来缩放单位球是重要的，因为它使得归一化在不同大小的向量之间更加鲁棒。

不变性分析

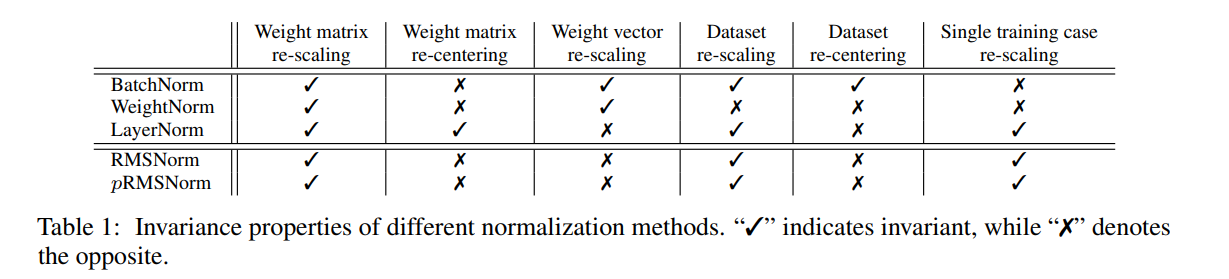
不变性衡量模型在归一化后输出是否高度按照其输入和权重矩阵变化。不同的归一化方法显示出不同的不变性属性，这对模型的稳健性贡献很大。

我们考虑RMSNorm的以下一般形式：
$$y=f\left(\frac{Wx\text{x}x}{\text{RMS}(a\text{a}a)}\odot g\text{g}g+b\text{b}b\right)\text{\hspace{1em}(5)}$$
其中$\odot$表示逐元素相乘。主要结果总结在表1中。由于RMS的以下线性性质，RMSNorm对于权重矩阵和输入的重新缩放都是不变的：
$$\text{RMS}(\alpha x\text{x}x)=\alpha \text{RMS}(x\text{x}x)\text{\hspace{1em}(6)}$$

其中$\alpha$是缩放值。假设权重矩阵通过一个因子$\delta$缩放，比如，$W^{\prime }=\delta W$，那么这个改变不会影响最终层输出：
$${y\text{y}y}^{\prime }=f\left(\frac{W^{\prime }x\text{x}x}{\text{RMS}({a\text{a}a}^{\prime })}\odot g\text{g}g+b\text{b}b\right)=f\left(\frac{\delta Wx\text{x}x}{\delta \text{RMS}(a\text{a}a)}\odot g\text{g}g+b\text{b}b\right)=y\text{y}y\text{\hspace{1em}(7)}$$
相比之下，如果仅对个别权重向量进行缩放，这个性质就不再成立，因为不同的缩放因子会破坏RMS的线性性质。同样地，如果我们强制对输入进行一个因子为$\delta$的缩放，比如${x\text{x}x}^{\prime }=\delta x\text{x}x$，通过与公式(7)类似的分析，RMSNorm的输出将保持不变。我们还可以轻松地将这个等式推广到基于批次的输入以及整个数据集。因此，RMSNorm对于其输入的缩放是不变的。

与LayerNorm的主要区别在于，RMSNorm没有重新居中，因此在变量偏移方面没有类似的线性性质。它不对所有重新居中操作都具有不变性。

梯度分析

上述分析仅考虑了输入缩放和权重矩阵对层输出的影响。然而，在一般情况下，通过标准的随机梯度下降方法来训练经过RMSNorm增强的神经网络，模型梯度的稳健性对于参数更新和模型收敛非常关键。

Santurkar等人认为归一化方法的成功并不是因为增加了对层输入的稳定性，而是由于优化过程的平滑性增加。

我们研究RMSNorm中模型梯度的性质。给定一个损失函数KaTeX parse error: Undefined control sequence: \cal at position 1: \̲c̲a̲l̲ ̲L，我们通过公式(4)进行反向传播，得到参数$g\text{g}g$、$b\text{b}b$的梯度如下：
$$\frac{\partial \mathcal{L}}{\partial b\text{b}b}=\frac{\partial \mathcal{L}}{\partial v\text{v}v},\frac{\partial \mathcal{L}}{\partial g\text{g}g}=\frac{\partial \mathcal{L}}{\partial v\text{v}v}\odot \frac{Wx\text{x}x}{\text{RMS}(a\text{a}a)}\text{\hspace{1em}(8)}$$
其中，$v\text{v}v$代表公式(4)中$f(\cdot )$内部的整个表达式，$\partial \mathcal{L}/\partial v\text{v}v$是从KaTeX parse error: Undefined control sequence: \cal at position 1: \̲c̲a̲l̲ ̲L到$v\text{v}v$的反向传播梯度。无论对于输入$x\text{x}x$的缩放还是对于权重矩阵$W$(对于$\partial \mathcal{L}/\partial g\text{g}g$来说，是因为公式(6)中的线性性质)，梯度KaTeX parse error: Undefined control sequence: \cal at position 2: ∂\̲c̲a̲l̲ ̲L/∂\pmb b和KaTeX parse error: Undefined control sequence: \cal at position 2: ∂\̲c̲a̲l̲ ̲L/∂\pmb g都是不变的。此外，$g\text{g}g$的梯度与归一化的输入之和成正比，而不是原始输入。这增强了$g\text{g}g$的幅度稳定性。

与这些向量参数不同，权重矩阵W的梯度由于RMS中的二次计算而更加复杂。具体来说，
$$\frac{\partial \mathcal{L}}{\partial W}=\sum _{i=1}^n\left[{x\text{x}x}^{\top }\otimes \left(\text{diag}\left(g\text{g}g\odot \frac{\partial \mathcal{L}}{\partial v\text{v}v}\right)\times R\right)\right]\text{\hspace{1em}(9)}$$
其中
$$R=\frac{1}{\text{RMS}(a\text{a}a)}=\left(I\text{I}I-\frac{(Wx\text{x}x)(Wx\text{x}x{)}^{\top }}{n\text{RMS}(a\text{a}a{)}^2}\right)\text{\hspace{1em}(9.1)}$$

$\text{diag}(\cdot )$表示输入的对角矩阵，$\otimes$表示克罗内克内积，而$I\text{I}I$​表示单位矩阵。

为了清晰起见，使用$\times$表示矩阵乘法。矩阵项$R$将$W$的梯度与输入$x\text{x}x$和权重矩阵$W$联系起来。通过彻底分析，我们可以证明该项与输入和权重矩阵的缩放呈负相关。在将输入$x\text{x}x（{x\text{x}x}^{\prime }=\delta x\text{x}x)$或权重矩阵$W^{\prime }=\delta W$分配一个因子$\delta$的尺度后，我们有以下关系：
$$R^{\prime }=\frac{1}{\delta \text{RMS}(a\text{a}a)}\left(I\text{I}I-\frac{(\delta Wx\text{x}x)(\delta Wx\text{x}x{)}^{\top }}{n{\delta }^2\text{RMS}(a\text{a}a{)}^2}\right)=\frac{1}{\delta }R\text{\hspace{1em}(10)}$$
如果我们将缩放后的$R^{\prime }$项放回到公式(9)中，可以轻松证明梯度$\partial \mathcal{L}/\partial W$对于输入缩放是不变的，但与权重矩阵的缩放呈负相关。

减少梯度$\partial \mathcal{L}/\partial W$​对于输入缩放的敏感性可以确保其平滑性，并提高学习的稳定性。另一方面，负相关作为一个隐式的学习率适应器，动态地控制梯度的范数，避免了范数较大的权重矩阵，提高了模型的收敛性。

结论

本文介绍了RMSNorm，保留了LayerNorm的重新缩放不变性属性，但舍弃了重新居中不变性属性。与LayerNorm相比，采用RMSNorm的模型的计算开销较小，可以作为LayerNorm的替代方案，轻松应用于不同的模型架构。

总结

⭐ 作者在层归一化的基础上移除掉均值相关项，得到了RMSNorm。然后通过实现证明其效果还不错。