决策树学习与实战

目录

什么是决策树？

1.举例：

2.程序实现思路

划分选择

1、信息熵

2、信息增益

3、增益率

4、基尼指数

剪枝处理

1.预剪枝

2.后剪枝

连续值与缺失值

连续值处理

缺失值处理

多变量决策树

决策树实战

---

什么是决策树？

决策树分类的思想类似于找对象。现想象一个女孩的母亲要给这个女孩介绍男朋友，于是有了下面的对话：

女儿：多大年纪了？   (年龄)

母亲：26。

女儿：长的帅不帅？   (长相)

母亲：挺帅的。

女儿：收入高不？       (收入情况)

母亲：不算很高，中等情况。

女儿：是公务员不？  (是否公务员)

母亲：是，在税务局上班呢。

女儿：那好，我去见见。

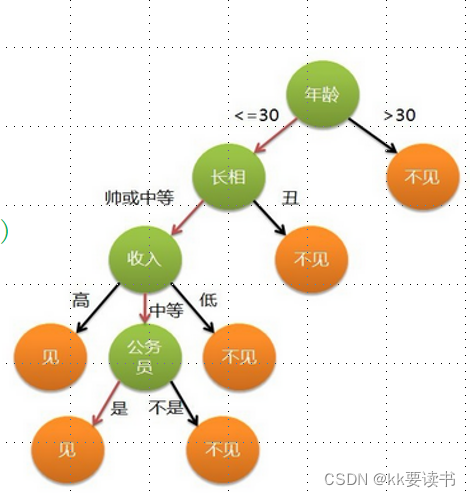
 分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点和有向边组成。结点有两种类型：内部结点和叶节点。内部结点表示一个特征或属性，叶节点表示一个类。

决策树学习的目的是为了产生一棵泛化能力强，即处理未见示例能力强的决策树

1.举例：

判断西瓜是不是好瓜，我们从 色泽 、 根蒂 、 敲声三个属性来判断

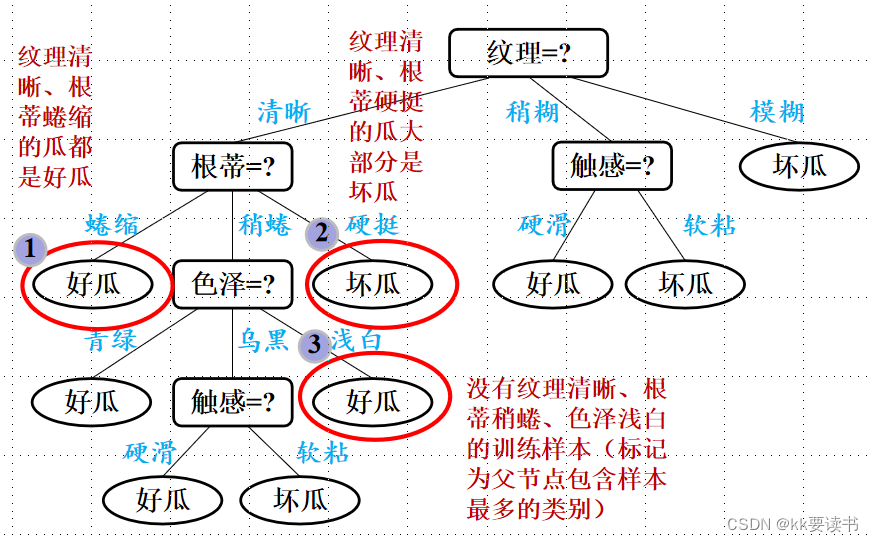
2.程序实现思路

决策树的生成是一个递归过程

递归结束条件有三种情况

情况1：当前结点所有样本都属于同一类别 （已经分好了）

情况2：当前结点所有样本在所有属性上取值相同（属性都一样，没法区分）

情况3：当前结点包含的样本集为空，不能划分（没有样本了，自然无法再分了）

划分选择

决策树的划分选择是指在构建决策树的过程中，如何选择最优的特征进行节点的划分。

即： 结点的“纯度”越来越高

1、信息熵

信息熵”是衡量样本集合纯度最常用的一种指标，信息熵的值越小，代表样本集合的纯度越高。

假定当前样本集合D中第k类样本所占的比例为 pk (K=1, 2, ..., |y|)   ，则D的信息熵定义为

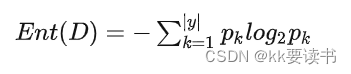
Ent(D)的值越小，则D的纯度越高。

例如：一共30个瓜，其中色泽为青绿、乌黑和浅白的分别有8,10,12个

2、信息增益

信息增益是一种用于选择最优划分特征的准则，它衡量了通过某个特征对样本进行划分后，整个系统的不确定性减少的程度。Ent（D）是“划分前的信息熵”，Ent（D|A）是“划分后的总信息熵”

即：

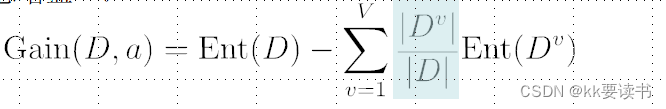
信息增益越大，意味着使用来划分所获得的“纯度提升”越大

3、增益率

增益率（Gain Ratio）是决策树算法中用于特征选择的一种准则，它对信息增益进行了修正，解决了信息增益对取值数目较多的特征有所偏好的问题。计算公式：增益率=信息增益​|分裂信息

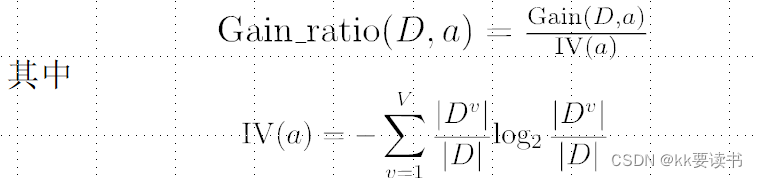
属性的可能取值数目越多（即V越大），则IV()的值通常就越大

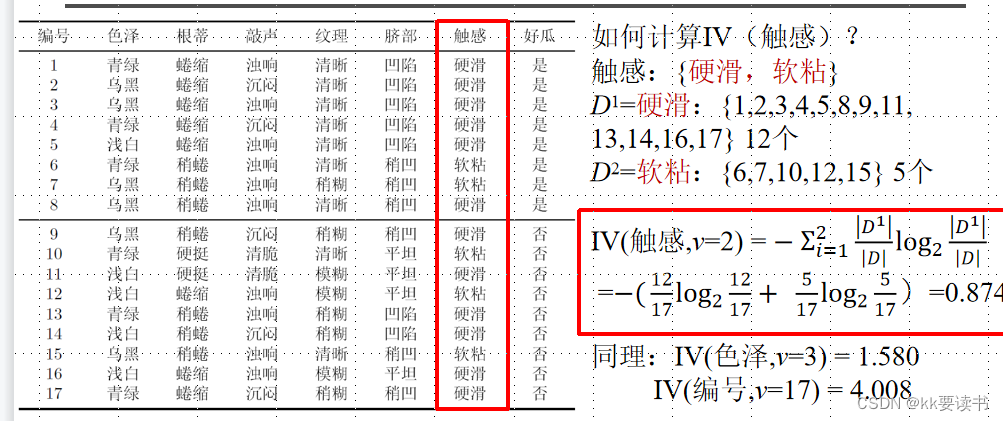
4、基尼指数

基尼指数（Gini index）是决策树算法中一种用于特征选择的准则，它衡量了通过某个特征对样本进行划分后，样本集合的不纯度（impurity）或混乱程度。基尼指数越小，表示样本集合的纯度越高，特征对分类的贡献越大。

比如属性A108，B39

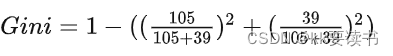
基尼指数的取值范围为 0 到 1，当样本集合完全纯净时（即只包含某个类别的样本），基尼指数为 0；当样本集合的每个类别的样本比例相等时，基尼指数最大，为 1−1/k。

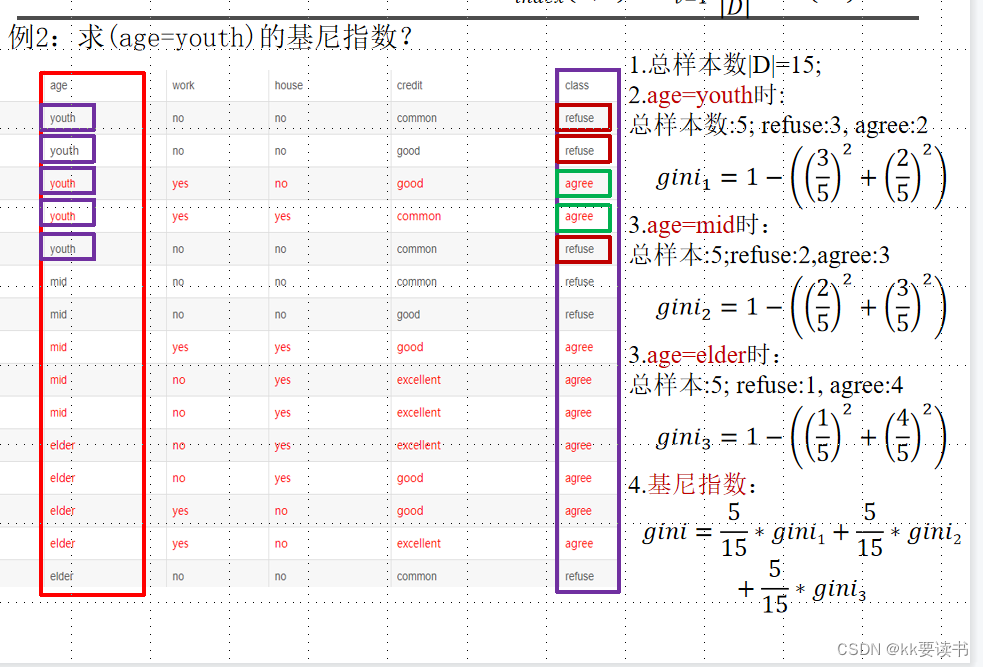
剪枝处理

剪枝是决策树学习算法对付“过拟合”的主要手段

1.预剪枝

看划分后能不能带来性能的提升，如果不能就不划分了

未剪枝

预剪枝

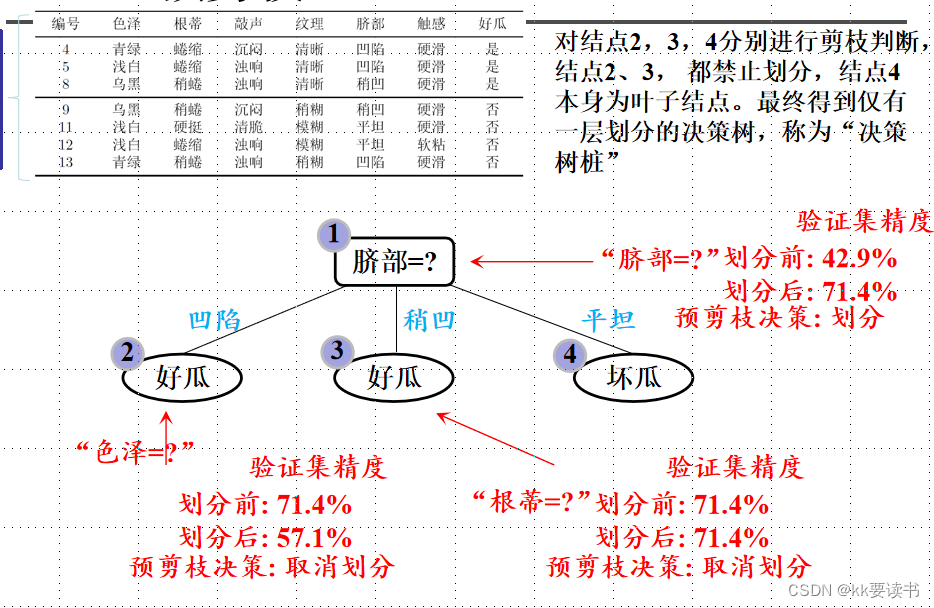
预剪枝虽然简单易于实现，但其可能会导致决策树欠拟合，即对训练数据的拟合程度较差，从而影响决策树的预测性能。预剪枝一般适用于数据集较小、噪声较大或者特征数目较多的情况下，以避免过拟合产生。

2.后剪枝

如果把分枝剪了，发现性能变好了，就把该分枝剪了

生成一棵完整的决策树（如上图未剪枝），然后自底向上地对非叶结点进行分析计算，若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升，则将该子树替换为叶结点。

考虑结点6

然后结点5,精度无改变可以不用剪枝，接着结点2

后剪枝的目的是通过减少决策树的规模，降低模型复杂度，以防止过拟合。相比于预剪枝，后剪枝在构建决策树时没有限制树的生长，因此可以更好地拟合训练数据。但是，后剪枝需要额外的验证集来评估修剪后的决策树的性能，并且修剪的过程相对复杂。

连续值与缺失值

连续值处理

将连续属性 a 在样本集 D 上出现 n 个不同的取值从小到大排列，记为 a1, a2, ..., an 。基于划分点t，可将D分为子集Dt+和Dt-，其中Dt-包含那些在属性a上取值不大于t的样本，Dt+包含那些在属性 a上取值大于t的样本。考虑包含n-1个元素的候选划分点集合。

  即把区间 [ai, ai-1) 的中位点 (ai+ai-1)/2作为候选划分点。

采用离散属性值方法，计算这些划分点的增益，选取最优的划分点进行样本集合的划分：

 其中Gain(D, a, t)是样本集D基于划分点 t 二分后的信息增益，于是， 就可选择使Gain(D, a, t)最大化的划分点。

缺失值处理

缺失值是指数据集中某些观测值或属性的值缺失或未记录。

在决策树中处理缺失值是一个重要的步骤，因为缺失值可能会影响模型的性能和准确性。以下是一些常用的处理缺失值的方法：

1. 删除缺失值：最简单的方法是直接删除包含缺失值的样本或特征。但是，这种方法可能会导致信息损失，并且在数据集较小的情况下可能会影响模型性能。

2. 使用默认值：对于数值型特征，可以用均值、中位数或众数等默认值来填充缺失值。对于类别型特征，可以用最常见的类别来填充缺失值。

3. 插值方法：可以使用插值方法来预测缺失值。常用的插值方法包括线性插值、多项式插值、样条插值等。这些方法可以根据已有的数据样本推断出缺失值。

4. 构建指示变量：对于类别型特征，可以将缺失值作为一个新的类别进行处理，即构建一个指示变量。这样可以保留缺失值的信息，并且不会引入偏差。

5. 使用模型预测：可以利用其他特征值构建一个模型，然后使用该模型来预测缺失值。例如，可以使用回归模型或分类模型来预测缺失值。

多变量决策树

多变量决策树是一种基于决策树算法的模型，用于处理具有多个输入变量的分类或回归问题。传统的决策树算法通常只考虑一个特征或变量来进行分割，而多变量决策树则可以同时考虑多个特征或变量来进行分割。

多变量决策树的主要思想是在每个节点上选择多个特征来进行划分，从而更准确地捕捉特征之间的相互关系。它通过比较不同特征组合的分割效果，选择最佳的特征组合来进行划分。这样可以提高模型的预测能力，并且能够处理特征之间的交互作用和高维数据。

在构建多变量决策树时，可以使用一些特定的算法或技术，如CART（Classification and Regression Trees）算法、随机森林（Random Forest）等。这些方法都可以在节点划分时同时考虑多个特征，并根据一定的准则选择最佳的特征组合。

多变量决策树在许多领域中都有应用，例如金融风险评估、医学诊断、自然语言处理等。它的优点包括能够处理复杂的关系和交互作用，具有较好的解释性和可解释性，同时还能够自动进行特征选择。

然而，多变量决策树也存在一些挑战和限制，例如容易出现过拟合问题、计算复杂度高等。因此，在应用多变量决策树时需要注意参数调节和模型评估，以及对数据进行适当的预处理和特征工程。

决策树实战

现在用波士顿房屋价格预测的案例来进行实战。我们将使用一个包含房屋面积、位置、卧室数量等特征的数据集，并通过构建一个决策树模型来预测未知房屋的价格。

1.数据集说明

scikit-learn 是基于Python 的一个机器学习库，简称为sklearn，其中实现了很多机器学习算法。我们可以通过sklearn 官方手册 来学习如何使用它。

我们使用sklearn 库的datasets 模块中自带的波士顿房价数据集：load_boston()，通过下面方式导入

from sklearn.datasets import load_boston
boston = load_boston()

在sklearn波士顿房价数据集中，重要的参数包括以下13个特征：

1. CRIM：城镇人均犯罪率
2. ZN：住宅用地所占比例
3. INDUS：城镇中非商业用地所占比例
4. CHAS：是否靠近Charles River的边界（如果是，则为1；否则为0）
5. NOX：一氧化氮浓度（每千万分之一）
6. RM：每栋住宅的平均房间数
7. AGE：1940年以前建成的自住单位比例
8. DIS：距离五个波士顿就业中心的加权距离
9. RAD：距离高速公路的便利指数
10. TAX：每万美元的不动产税率
11. PTRATIO：学生与教师的比例
12. B：黑人比例（以1000(Bk - 0.63)^2计算）
13. LSTAT：较低地位人口的百分比。

2.导入所需要的包

from sklearn.datasets import load_boston
from sklearn.tree import DecisionTreeRegressor, plot_tree
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt

3.数据集划分

X变量表示数据集的特征部分，包含了13个特征（如前面所提到的）组成的二维数组。y变量表示数据集的目标变量，即房价，是一个一维数组，使用train_test_split()函数将数据集划分为训练集和测试集。

boston = load_boston()
X = boston.data
y = boston.target
 
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42

3.构建决策树模型
​​​​​

# 构建决策树模型并设置最大深度为5
clf = DecisionTreeRegressor(max_depth=5)
 
# 训练模型
clf.fit(X_train, y_train)

模型得分Accuracy: 100.00%

4.打印决策树

# 可视化决策树
fig, ax = plt.subplots(figsize=(15,10))
plot_tree(clf, filled=True, feature_names=boston.feature_names)
plt.show()

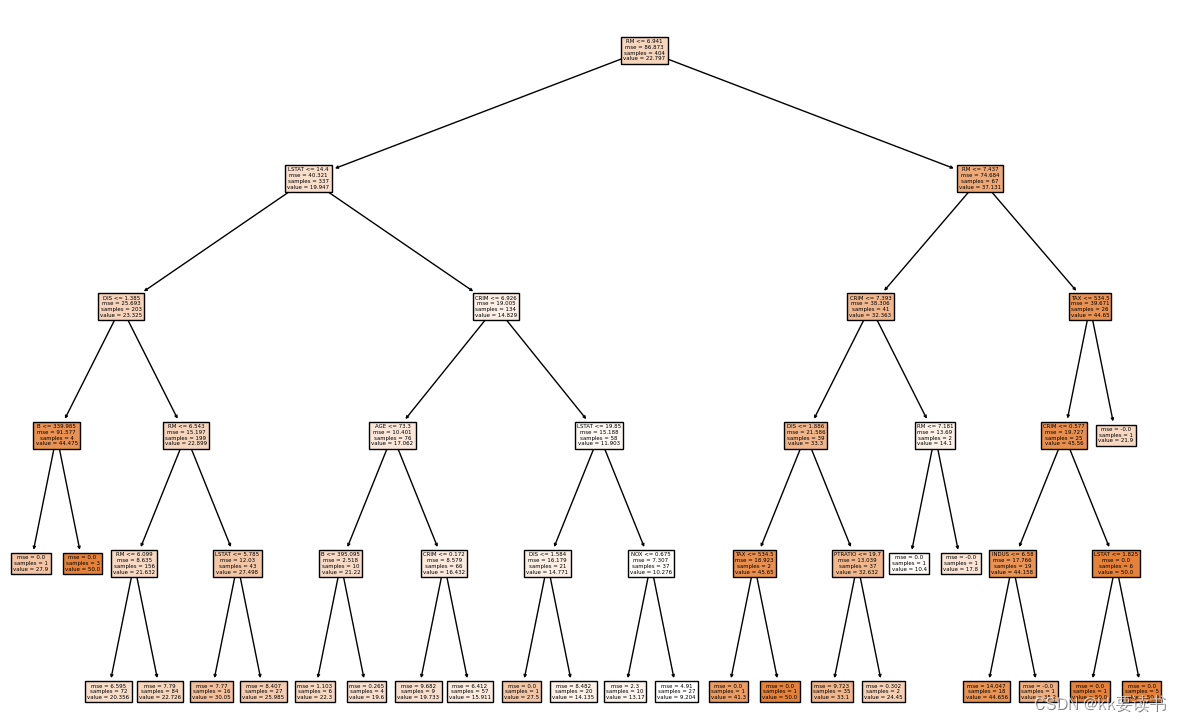
节点太多，我们可以先查看属性对应的重要性的数值

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestRegressor
 
# 加载波士顿房价数据集
boston = load_boston()
X = boston.data
y = boston.target
 
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
 
# 创建并训练随机森林回归模型
model = RandomForestRegressor()
model.fit(X_train, y_train)
 
# 获取属性重要性数值
importance = model.feature_importances_
 
# 将属性重要性数值与属性名称对应起来
feature_names = boston.feature_names
feature_importance = dict(zip(feature_names, importance))
 
# 打印每个属性的重要性数值
for feature, importance in feature_importance.items():
    print(f"{feature}: {importance}")

将有下面输出

CRIM: 0.049352244609685306
ZN: 0.0015039071811990308
INDUS: 0.006550118681426682
CHAS: 0.0013304043055677407
NOX: 0.017250456850065733
RM: 0.3752577747841356
AGE: 0.01808575495930588
DIS: 0.06122847662028567
RAD: 0.0049787240161058235
TAX: 0.01223464447852929
PTRATIO: 0.01837228820171694
B: 0.012023325898140243
LSTAT: 0.412380839493071

4.调参确认最佳剪枝参数并重新训练模型

在不加限制的情况下，一棵决策树会生长到衡量不纯度的指标最优，或者没有更多的特征可用为止。这样的决策树 往往会过拟合，这就是说， 它会在训练集上表现很好，在测试集上却表现糟糕 。

# 导入GridSearchCV库用于寻找最优参数
from sklearn.model_selection import GridSearchCV
 
# 定义参数范围
param_grid = {'max_depth': range(1, 11)}
 
# 使用GridSearchCV寻找最优参数
grid_search = GridSearchCV(DecisionTreeRegressor(), param_grid, cv=10)
grid_search.fit(X_train, y_train)
 
# 输出最优参数
print("最优参数: {}".format(grid_search.best_params_))
 
# 使用最优参数重新训练模型
clf = DecisionTreeRegressor(max_depth=grid_search.best_params_['max_depth'])
clf.fit(X_train, y_train)
 
# 在测试集上进行预测
y_pred = clf.predict(X_test)
 
# 计算均方误差
mse = mean_squared_error(y_test, y_pred)
 
# 打印结果
print("均方误差：{:.2f}".format(mse))

均方误差：8.55

总结

决策树模型具有易于理解、解释和可视化的特点，能够处理多分类问题，并且对缺失数据有一定的容错性。同时，决策树模型也存在一些缺点，如容易过拟合、对噪声敏感等问题，需要注意在模型选择和调参时进行充分的考虑。