人工智能——分类器性能指标之ROC曲线、AUC值_classifier roc auc

二分类模型预测的结果是否足够好，ROC和AUC是重要指标。

ROC曲线

ROC曲线概念

ROC曲线：接收者操作特征(receiveroperating characteristic)，roc曲线上每个点反映着对同一信号刺激的感受性。

ROC曲线坐标系

横轴：负正类率(false postive rate FPR)特异度，划分实例中所有负例占所有负例的比例；(1-Specificity)

纵轴：真正类率(true postive rate TPR)灵敏度，Sensitivity(正类覆盖率)

ROC曲线重要概念

针对一个二分类问题，将实例分成正类(postive)或者负类(negative)。但是实际中分类时，会出现四种情况.

1. 若一个实例是正类并且被预测为正类，即为真正类(True Postive TP)
2. 若一个实例是正类，但是被预测成为负类，即为假负类(False Negative FN)
3. 若一个实例是负类，但是被预测成为正类，即为假正类(False Postive FP)
4. 若一个实例是负类，但是被预测成为负类，即为真负类(True Negative TN)

这四种情况在深度学习的结果中又代表如下情况

• TP:正确的肯定数目

• FN:漏报，没有找到正确匹配的数目

• FP:误报，没有的匹配不正确

• TN:正确拒绝的非匹配数目

列联表如下，1代表正类，0代表负类：

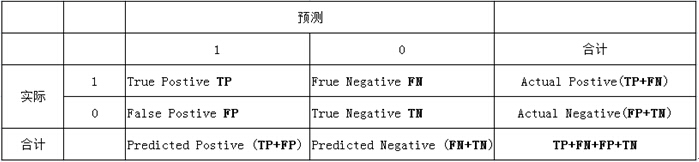
由上表可得出横，纵轴的计算公式：

• 真正类率(True Postive Rate)TPR: TP/(TP+FN),代表分类器预测的正类中实际正实例占所有正实例的比例。Sensitivity
• 负正类率(False Postive Rate)FPR: FP/(FP+TN)，代表分类器预测的正类中实际负实例占所有负实例的比例。1-Specificity
• 真负类率(True Negative Rate)TNR: TN/(FP+TN),代表分类器预测的负类中实际负实例占所有负实例的比例，TNR=1-FPR。Specificity

特异度(specificity)与灵敏度(sensitivity)

假设采用逻辑回归分类器，其给出针对每个实例为正类的概率，那么通过设定一个阈值如0.6，概率大于等于0.6的为正类，小于0.6的为负类。对应的就可以算出一组(FPR,TPR),在平面中得到对应坐标点。随着阈值的逐渐减小，越来越多的实例被划分为正类，但是这些正类中同样也掺杂着真正的负实例，即TPR和FPR会同时增大。阈值最大时，对应坐标点为(0,0)，阈值最小时，对应坐标点(1,1)。

如下面这幅图，(a)图中实线为ROC曲线，线上每个点对应一个阈值。

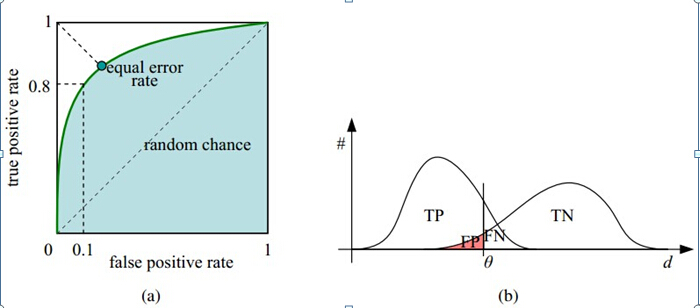
横轴FPR:1-TNR,1-Specificity，FPR越大，预测正类中实际负类越多。

纵轴TPR：Sensitivity(正类覆盖率),TPR越大，预测正类中实际正类越多。

理想目标：TPR=1，FPR=0，即图中(0,1)点，故ROC曲线越靠拢(0,1)点，越偏离45度对角线越好，Sensitivity、Specificity越大效果越好。

案例：画ROC曲线

假设已经得出一系列样本被划分为正类的概率，然后按照大小排序，下图是一个示例，图中共有20个测试样本，“Class”一栏表示每个测试样本真正的标签（p表示正样本，n表示负样本），“Score”表示每个测试样本属于正样本的概率。

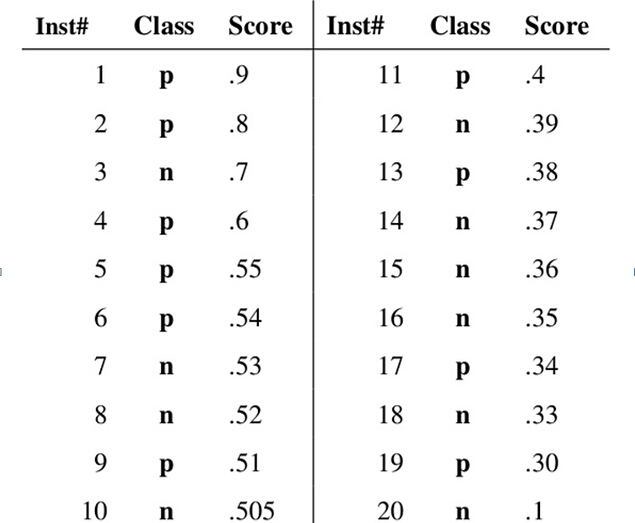
接下来，我们从高到低，依次将“Score”值作为阈值threshold，当测试样本属于正样本的概率大于或等于这个threshold时，我们认为它为正样本，否则为负样本。

举例来说，对于图中的第4个样本，其“Score”值为0.6，那么样本1，2，3，4都被认为是正样本，因为它们的“Score”值都大于等于0.6，而其他样本则都认为是负样本。每次选取一个不同的threshold，我们就可以得到一组FPR和TPR，即ROC曲线上的一点。这样一来，我们一共得到了20组FPR和TPR的值，将它们画在ROC曲线的结果如下图：

AUC值

AUC(Area under Curve)：Roc曲线下的面积，介于0.1和1之间。Auc作为数值可以直观的评价分类器的好坏，值越大越好。

首先AUC值是一个概率值，当你随机挑选一个正样本以及负样本，当前的分类算法根据计算得到的Score值将这个正样本排在负样本前面的概率就是AUC值，AUC值越大，当前分类算法越有可能将正样本排在负样本前面，从而能够更好地分类。

为什么使用Roc和Auc评价分类器

既然已经这么多标准，为什么还要使用ROC和AUC呢？因为ROC曲线有个很好的特性：当测试集中的正负样本的分布变换的时候，ROC曲线能够保持不变。在实际的数据集中经常会出现样本类不平衡，即正负样本比例差距较大，而且测试数据中的正负样本也可能随着时间变化。下图是ROC曲线和Presision-Recall曲线的对比：

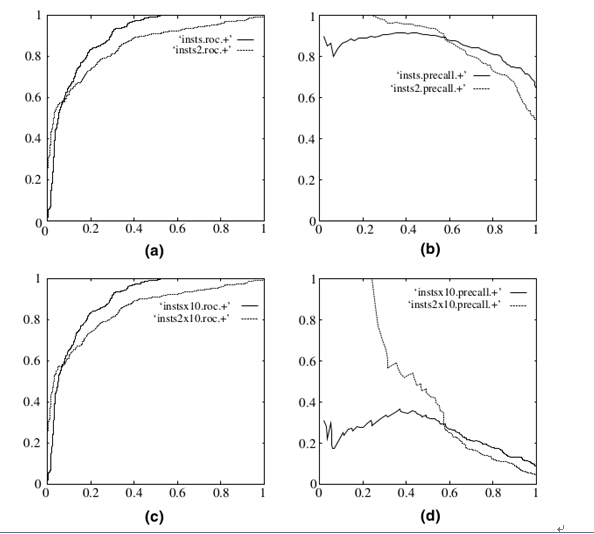
在上图中，(a)和©为Roc曲线，(b)和(d)为Precision-Recall曲线。

(a)和(b)展示的是分类其在原始测试集(正负样本分布平衡)的结果，©(d)是将测试集中负样本的数量增加到原来的10倍后，分类器的结果，可以明显的看出，ROC曲线基本保持原貌，而Precision-Recall曲线变化较大。