Python机器学习--分类\回归--决策树算法_决策树回归与分类算法

决策树算法类型

决策树是一系列算法，而不是一个算法。
决策树包含了 ID3分类算法，C4.5分类算法，Cart分类树算法，Cart回归树算法。
决策树既可以做分类算法，也可以做回归算法。因此决策树既可以解决分类问题，也可以解决回归问题。

一般来讲，在决策树中，根节点和分节点使用方块表示，而叶子节点使用椭圆表示。
决策树的关键点在于如何取建立出一个树，如何建立出一个在可以达成目标的前提下深度最浅的树

决策树中不同算法的介绍

CLS、ID3、C4.5、CART四种，其中ID3、C4.5、CART都采用贪心方法，其中决策树以自顶向下递归的分治方法构造，并且大多数决策树算法都采用这种自顶向下的方法。所谓贪心方法，通俗的讲就是在选取根节点时把所有的都计算一遍，使用穷举的方法找到最优

CLS算法简介

CLS是最早期的决策树算法，它并没有给出怎样确定根节点，只是给出了创建决策树的具体方法，其他三种算法是对CLS的优化和延伸。
CLS的基本流程：

• 生成一棵空的决策树和一个训练集样本属性集。
• 若训练集中所有样本都属于同一类，则生成一个叶子节点，终止算法。
• 根据某种策略从训练集样本的属性中选择属性作为分裂属性，生成测试节点。
• 根据测试节点的取值不同分为不同的的分支。
• 从训练样本的属性中删除已经分裂过的属性。
• 辗转至步骤 2 重复操作，直到分裂出所有的数据都属于同一类停止。

通俗点讲：

CLS就是从数据集中随机选择一列（等意于一个特征或一个属性），如果他所有的取值都属于同一类别，就终止，否则删除该列，再根据删除的列的取值分支进行分裂，直至所有的分裂都属于同一类别。

ID3分类算法简介

ID3主要针对于属性选择问题，使用信息增益来选择分裂属性的评断标准

ID3分类算法特点：

1. 只能实现分类算法
2. 特征必须是离散数据
3. 树是可以多分支（多叉树）---一个特征属性 有多个取值，每个取值是一个分支
4. 是多分类算法[标签数量可以大于2 活动的结果：进行 or 取消  or 暂定 ] 

ID3分类算法缺点:

优先选择属性取值多的特征进行分裂

什么是信息增益熵？

信息量的计算公式：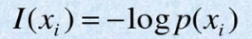

信息出现的概率越大，表示它信息量就越少，即出现概率越小，信息量越大。比如当概率等于1时，信息量就等于 -log(1)

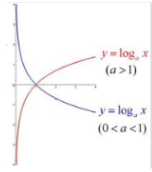
在信息论中，通常指数是以2为底，因此只需考虑图中的红色线即可。

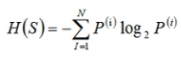
对于熵的理解可以简化为 加权平均信息量。特征S的取值有N种，而每种可能出现的概率乘以他的信息量并相加就是加权平均信息量。

条件熵 

相当于条件概率
1.先计算结果的熵值。
2.在计算已知某特征条件下的结果结果的熵值。

举例：
假设某 特征存在三个取值，标签有两个取值。
1.先计算出该特征三个取值的概率：p1,p2,p3.
2.计算每一个取值下结果的熵值。
3.条件熵=三个取值结果下的三个熵值的加权平均。

ID3分类算法信息增益

信息增益的作用就是确定作为根节点的特征，用结果的熵值减去已知特征的情况下结果的条件熵计算公式：

Gain(特征) = H(结果) - H( 结果 | 特征 )
结论：选择信息增益最大的作为根节点

总结：
1.假设存在一个包含若干特征，一个标签的数据集。
2.对标签计算出结果熵值。
3.对所有特征中的取值计算出对应结果的条件熵。
4.计算每个特征的信息增益，选出最大值作为根节点。
5.将分裂完成的特征列删除，如果结果为同一类，结束算法。
6.如果不是同一类，则继续计算剩下的特征的信息增益，选取最大的作为下一次分裂的特征。
7.重复计算信息增益，选择特征进行分裂，直到所有叶子节点为同一类结束。

 ID3分类算法原理计算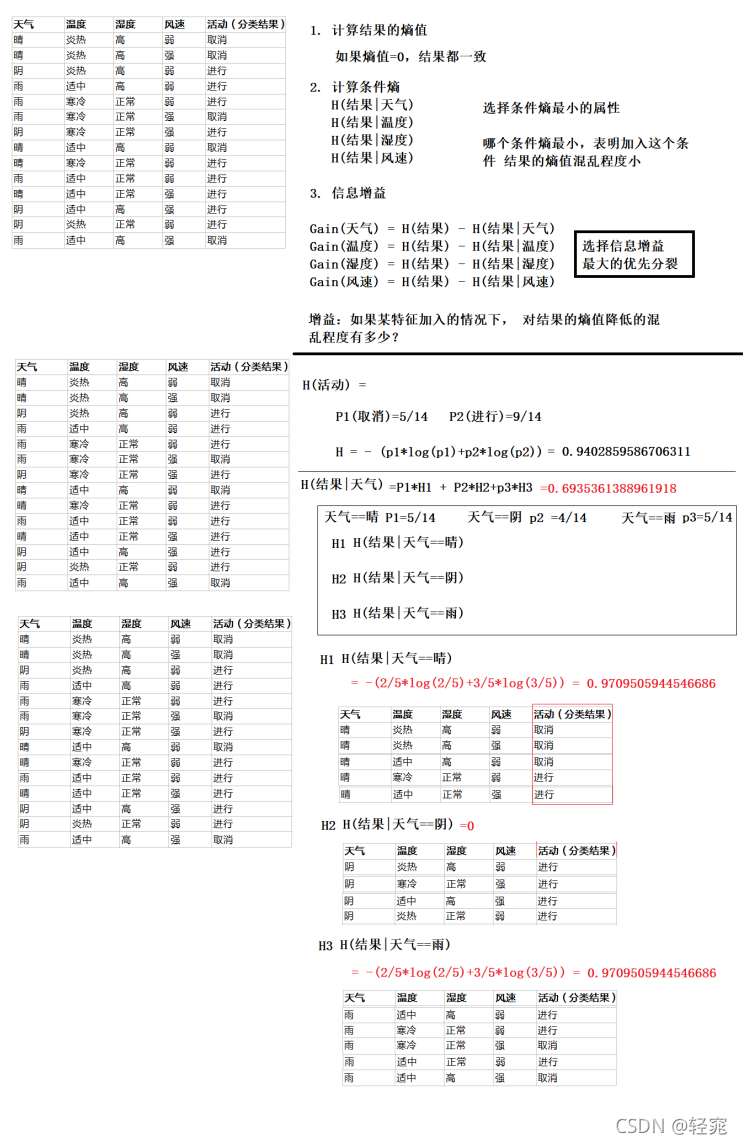

C4.5分类算法简介

在ID3的基础上做了一些优化，通过使用信息增益率选择分裂属性，克服了ID3算法中通过信息增益无法处理很多属性值的数据的缺陷，信息增益率能够处理离散数据和连续数据，还能处理有确实属性的训练数据。

C4.5分类算法的特点

1. 使用  信息增益率 作为分裂属性的评断标准
2. 只能实现分类算法
3. 能够处理连续数据的特征
4. 树是可以多分支（多叉树）
5. 是多分类算法 

C4.5分类算法信息增益率（Gainratio）

信息增益率能够有效避免倾向于选择拥有多个属性值的样本
信息增益率公式：
Gainratio(特征) = Gain(特征) / H(特征)
选择增益率最大的特征作为根节点，使用流程和使用信息增益的流程一样

C4.5分类算法连续值处理

对于连续型数据的处理，不再使用信息增益率处理，而使用下面的这种方式：

1. 假设某一特征中存在N个连续型数据。
2. 将这一列数据去重后升序排序。
3. 求出相邻两个值的均值，这样可以得到N-1个数据。
4. 先使用第一个数据，计算小于第一个数据的值的条件熵和大于第一个数据的条件熵，在计算出该数据的信息增益。
5. 以此计算剩下N-2个数据的信息增益。
6. 当比较信息增益，选择最大的信息增益对应的属性值作为分裂点（比如有一列为密度的特征，当密度=0.318时信息增益是最大的，选择这个点为分裂点，这是它的取值就变成了小于0.318的和大于等于0.318的两类，再进行分裂)
7. 

 

C4.5分类算法缺点

通过上述处理，只能将连续特征进行二分处理，依然是只能实现分类算法，下面的算法又进行了改进，可以实现处理分类算法和回归算法。

C4.5分类算法原理计算

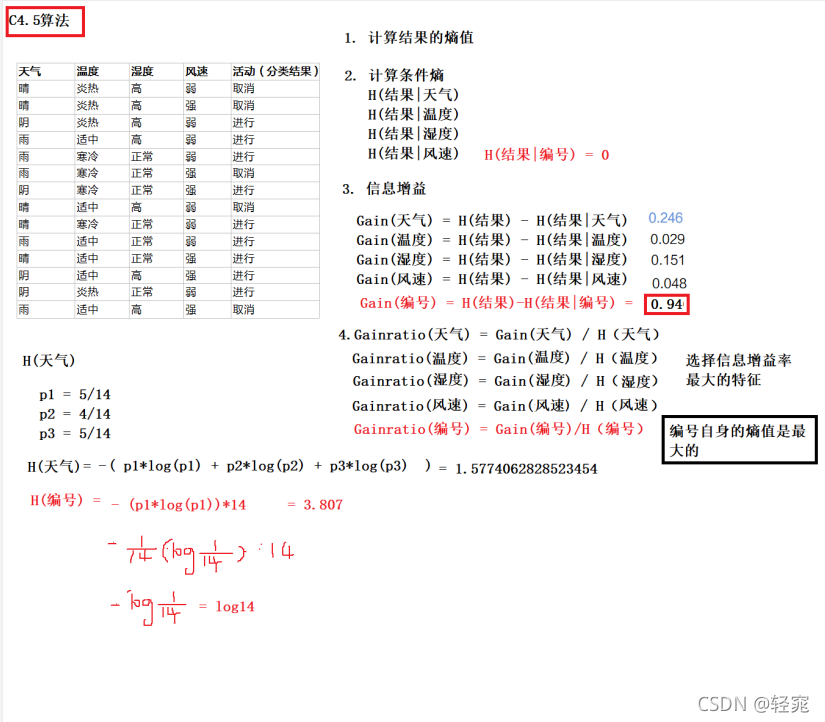
C4.5分类算法总结

信息增益率可以处理属性值特别多的特征；离散数据在经过分裂后会被删除，但是经过连续值处理后的数据分裂后不会被删除，后续还能作为属性划分。

CART分类算法基尼系数

基尼系数公式：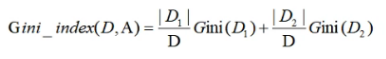

基尼值代表了模型的不纯度，基尼值越小，则不纯度越低，特征越好。基尼值=样本被选中的概率-样本被分错的概率，用公式表示为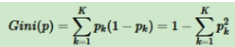         

基尼系数针对的是二分类，只会分为是或否。对于某一个特征，特征里面的所有取值都要计算一下对应结果的基尼值，然后计算基尼系数，选取最小的作为分裂节点

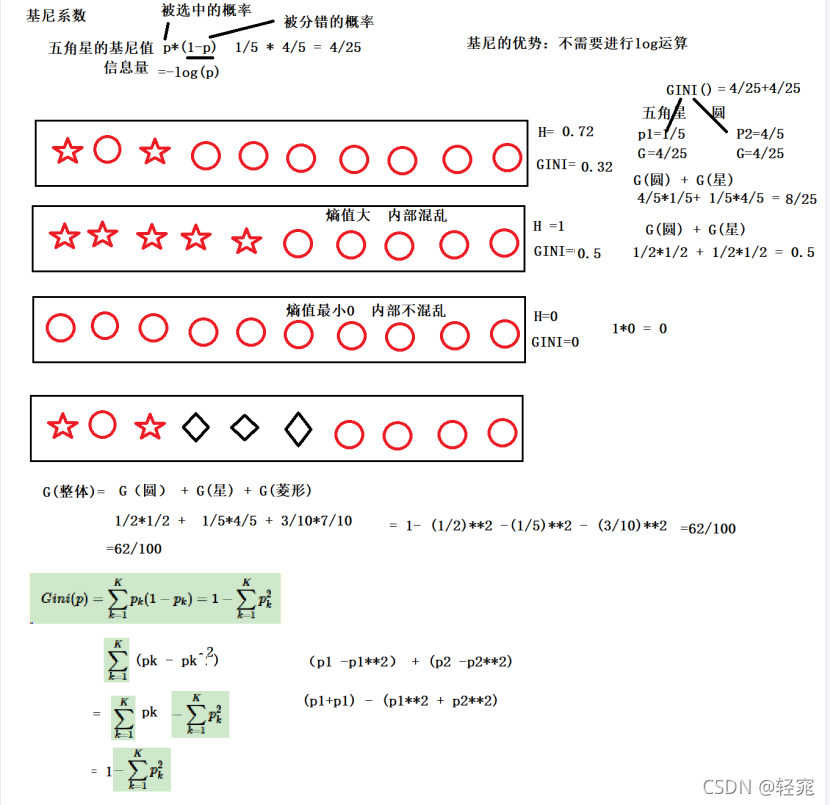
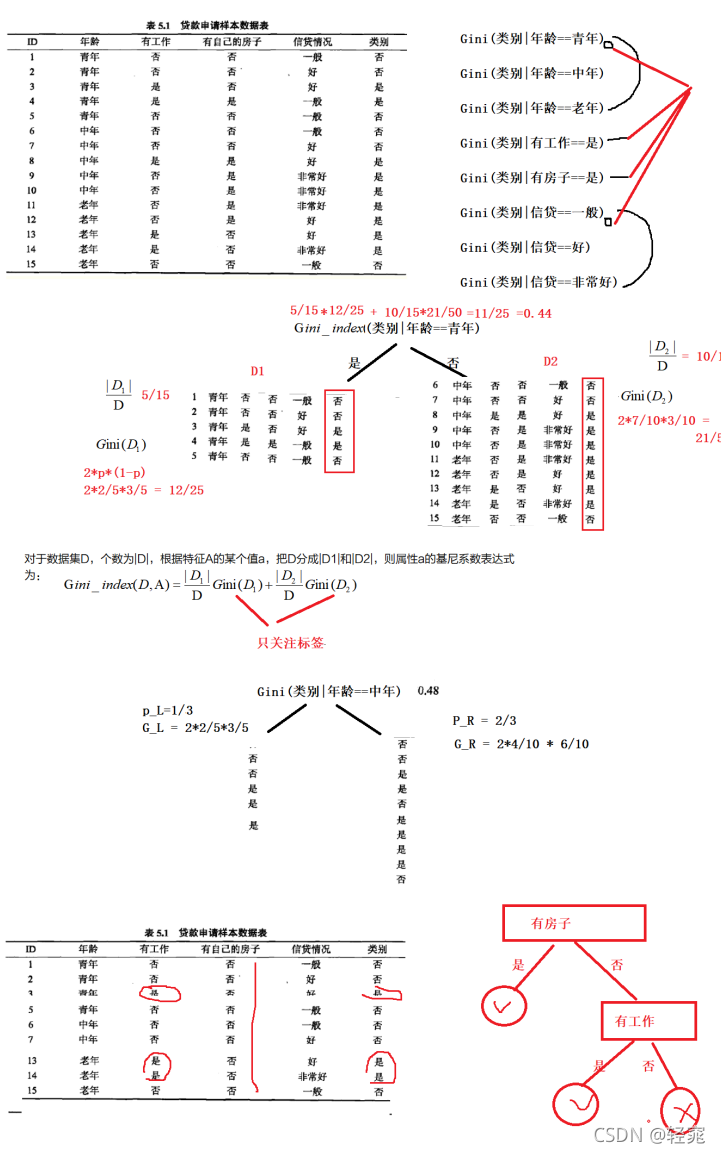
基尼系数只能在分类算法中使用

CART回归算法简介

CART回归算法平方误差

使用平方误差计算的是二分类回归算法，对连续性的标签进行处理，具体步骤为：

1. 先选取某一个特征的若干个取值进行计算，类似于条件熵，在已知取值的情况下结果的平均误差。
2. 选取平均误差小的作为分裂节点。
3. 在判断左节点如果小于等于三条，则终止左子树的分裂，如果大于3，就继续判断该节点的变换系数，如果小于0.1就停止左子树分裂，否则继续分裂，右子树同理。
4. 删除分裂过的特征，继续判断剩下的特征哪个取值平均误差最小。
5. 直到变换系数小于0.1或行数小于3时停止，如果停止时标签仍然有两个以上的值，那么就取其均值作为结果。

CART回归算法原理计算

平方误差计算流程：

• 因为是二分类，所以只分为是和否，分类为是的计算出平均误差加上分类为否的平均误差就是该节点平均误差。平均误差的公式为：( X - X均值 )**2，也可称为N次方差

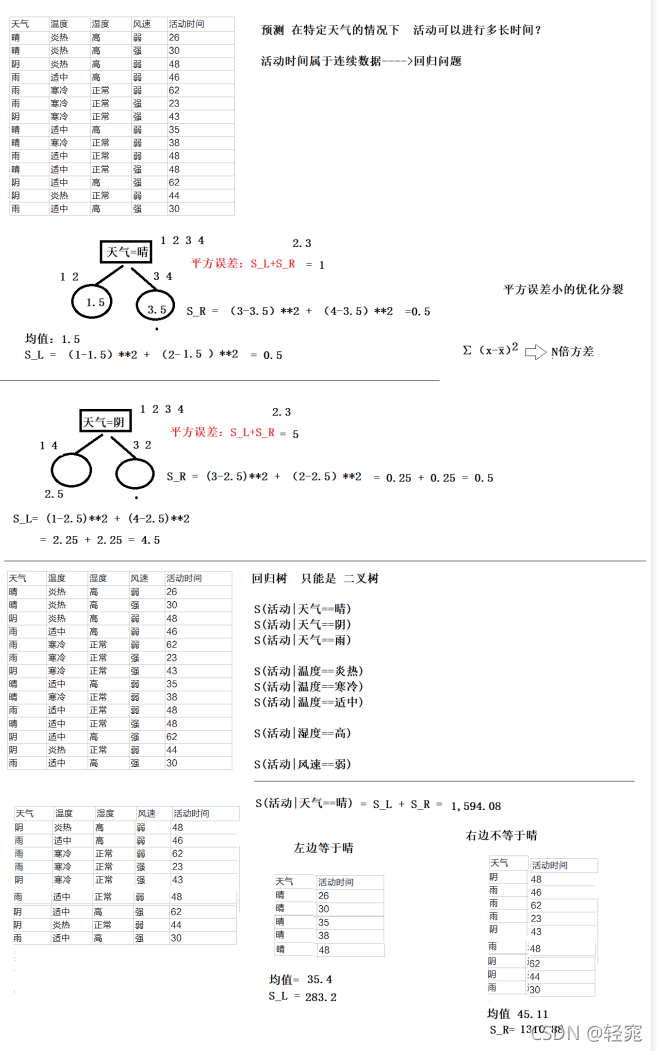
变换系数计算流程：

•  变换系数也称为离散系数或者变化系数，离散系数等于标准差除以均值，但是在平均误差中使用的是平均误差除以均值。

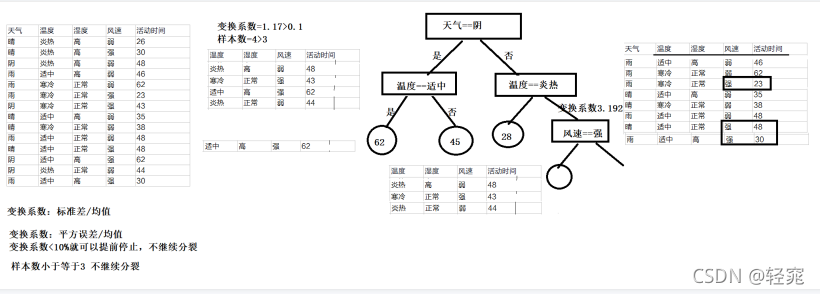
CART回归算法缺失值处理

在缺失值处理中使用最多的就是权重，下面以信息增益为例：

1. 比如某一特征有缺失值，在计算该列的信息增益时要先把有缺失值的行去掉，计算剩下的行信息增益
2. 其余特征有缺失值也是这样计算
3. 通过对比计算出的信息增益，选择最大的作为根节点，但是这只是选择根节点的方法
4. 选择出根节点后，根据取值进行分裂
5. 比如根节点列有两个缺失值，分了三个分支，每个分支上的数据数目分别为7，5，3；这个时候要把缺失值加回来，因为缺失值对应的行还有结果信息，后续选择还需要使用，每个分支都要加上两个缺失值，三个分支上的数据就变成了9，7，5；
6. 数据每一行的权重都是1，但是有缺失值就不一样了，由于每个分支上的无缺失数据有7，5，3；两个缺失值的权重就变成了：分支数据个数/(7+5+3+2)，也就是7/15，5/15，3/15，无缺值的权重还是1
7. 
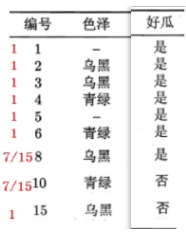
8. 在根据权重分别计算剩余特征的信息增益，去除要计算特征的缺失值，首先计算结果的熵，H(结果) = -p1log(p1) - p2log(p2)，公式中的概率p需要根据权重来计算，p = 非缺失值权重 / 总权重 ，p1 = (4 + 7/15) / (5 + 2 * 7/15)，条件熵的计算同理，再选择信息增益最大的进行分裂，重复加权计算的过程

缺失值的处理还是比较麻烦的，在数据量足够多的情况下，还是建议直接删除有缺失的行

决策树基于sklearn实现
决策树特点
使用垂直于特征值进行分裂
可以产生树结构，可视化效果好【0基础人可以理解算法预测过程】
不需要标准化
可以自动忽略掉对目标没有贡献的属性

CART分类\回归算法区别

CART可以实现分类和回归算法，sklearn中分别为Classification 和Regression Tree

CART算法特点
分类算法中使用基尼系数，作为分裂属性的评断标准。
回归算法中使用平法误差，作为分裂属性的评断标准。
树是二叉树。
是多分类算法
基尼与熵的关系：基尼与熵的趋势一致，基尼也成为熵之半，因此基尼的运算更加简单。

决策树-分类树基于sklearn实现

import pandas as pd
from sklearn.model_selection import train_test_split
#分类树
from sklearn.tree import DecisionTreeClassifier
 
#数据集的读取
work_data=pd.read_csv('./HR_comma_sep.csv')
work_data['department1']=work_data['department'].astype('category').cat.codes
work_data['salary1']=work_data['salary'].astype('category').cat.codes
x=work_data[['satisfaction_level', 'last_evaluation', 'number_project','average_montly_hours', 'time_spend_company', 'Work_accident','promotion_last_5years', 'department1','salary1']]
y=work_data['left']
 
#数据拆分
X_train, X_test, y_train, y_test = train_test_split(
    x,  # 特征
    y,  # 标签
    test_size=0.2,  # 给测试集分配多少数据
    random_state=1,
    stratify=y,  # 分层  保证拆分前后各类别的比例一致
)
 
#决策树
start_time=time.time()
dt = DecisionTreeClassifier()
dt.fit(X_train,y_train)
print("决策树预测准确率", dt.score(X_test, y_test))
end_time=time.time()
print("决策树用时", end_time-start_time)
 

决策树-回归树基于sklearn实现

import pandas as pd
from sklearn.model_selection import train_test_split
#回归树
from sklearn.tree import DecisionTreeRegressor
#数据的获取
selery_data=pd.read_excel('./job.xlsx',sheet_name=1)
name = selery_data['语言'].astype("category").cat.categories
selery_data['语言1']=selery_data['语言'].astype("category").cat.codes
selery_data['学历1']=selery_data['学历'].astype("category").cat.codes
x1=selery_data[['语言1','工作经验(年)','学历1']].values
y1=selery_data['最高薪资(元)'].values
#数据的拆分
X_train1, X_test1, y_train1, y_test1 = train_test_split(
    x1,  # 特征
    y1,  # 标签
    test_size=0.2,  # 给测试集分配多少数据
    random_state=1,
    # stratify=y1,  # 分层  保证拆分前后各类别的比例一致
)
#回归树
dt=DecisionTreeRegressor()
alg.fit(X_train1, y_train1)
print("回归树准确率", alg.score(X_test1, y_test1))

决策树最优参数的寻找

import pandas as pd
from sklearn.model_selection import train_test_split
#分类树
from sklearn.tree import DecisionTreeClassifier
#网格搜索
from sklearn.model_selection import GridSearchCV
 
#数据集的读取
work_data=pd.read_csv('./HR_comma_sep.csv')
work_data['department1']=work_data['department'].astype('category').cat.codes
work_data['salary1']=work_data['salary'].astype('category').cat.codes
x=work_data[['satisfaction_level', 'last_evaluation', 'number_project','average_montly_hours', 'time_spend_company', 'Work_accident','promotion_last_5years', 'department1','salary1']]
y=work_data['left']
 
#数据拆分
X_train, X_test, y_train, y_test = train_test_split(
    x,  # 特征
    y,  # 标签
    test_size=0.2,  # 给测试集分配多少数据
    random_state=1,
    stratify=y,  # 分层  保证拆分前后各类别的比例一致
)
#网格搜索最优参数探索
dt = DecisionTreeClassifier()
param_grid = {"criterion": ["gini", "entropy"], "max_depth": [3, 5, 6, 7, 9]}
gird = GridSearchCV(dt, param_grid)
gird.fit(X_train, y_train)
print("最好的参数", gird.best_params_)
 
#交叉验证探索最优参数
from sklearn.model_selection import cross_val_score
for max_depth in [3, 5, 6, 7, 9]:
    for criterion in ["gini", "entropy"]:
        dt = DecisionTreeClassifier(max_depth=max_depth, criterion=criterion)
        score = cross_val_score(dt, X_train, y_train, cv=5).mean()
        # print(score)
        print("深度是{} 准则{} 得分是{}".format(max_depth, criterion, score))
 
 
 
#分类树
start_time=time.time()
dt = DecisionTreeClassifier()
dt.fit(X_train,y_train)
print("决策树预测准确率", dt.score(X_test, y_test))
end_time=time.time()
print("决策树用时", end_time-start_time))

决策树输出树

 
 
 
# 将算法模型dt 导出到 dot文件中
from sklearn.tree import export_graphviz
export_graphviz(dt, 'titanic.dot',
                feature_names=["pclass", "age", "sex"],
                feature_names=["舱位", "年龄", "性别"],
                max_depth=5,  # 树的深度
                class_names=['死亡', '生存']  # 类别名称
)
 
#使用以下命令将生成的 titanic.dot转为图片格式
# dot -Tpng tree.dot -o tree.png