动态规划9：最长递增子序列、最长连续递增序列、最长重复子数组、最长公共子序列、不相交的线、最长子序和_最多删除一个元素的最长连续递增子序列

41. 最长递增子序列

例题300：
给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

动态规划

1. 确定dp数组和下标含义
   dp[i]表示在第i个元素的最长子序列数
2. 确定递推公式
   dp[i]应该是由dp[j]决定，也就是两层循环，第1层遍历数组每个元素，第2层遍历该元素下的子数组。
   dp[i]=Math.max(dp[i],dp[j]+1)
3. 初始化
   dp=1
4. 确定遍历顺序
   从前往后

代码如下：

时间复杂度O(n^2)，空间复杂度O(n)
class Solution {
    public int lengthOfLIS(int[] nums) {
        int n=nums.length;
        if(n==1) return 1;
        if(n==0) return 0;
        int[] dp=new int[n];
        int res=0;
        Arrays.fill(dp,1);
        for(int i=1;i<n;i++){
            for(int j=0;j<i;j++){
                if(nums[i]>nums[j])
                {
                dp[i]=Math.max(dp[i],dp[j]+1);
                }
                res=Math.max(res,dp[i]);
            }
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

进阶：时间复杂度O(nlgn)
贪心+二分法
为了让递增子序列最长，需要让子序列增长得慢。
当找到nums[i]>d[len]时，将nums[i]加入d数组；
当nums[i]<d[len]时，找到d中第一个小于nums[i]的数，将该数后一个改为nums[i]。

class Solution {
    public int lengthOfLIS(int[] nums) {
        int n=nums.length;
        if(n==1) return 1;
        if(n==0) return 0;
        int len=1;
        int[] d=new int[n+1];
        d[len]=nums[0];
        for(int i=1;i<n;i++){
            if(nums[i]>d[len]){
                len++;
                d[len]=nums[i];
            }
            else{
                int l=1,r=len,pos=0;
                while(l<=r){
                    int mid=(l+r)/2;
                    if(d[mid]<nums[i]){
                        pos=mid;
                        l=mid+1;给定一个未经排序的整数数组，找到最长且 连续递增的子序列，并返回该序列的长度。

连续递增的子序列 可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。
                    }
                    else{
                        r=mid-1;
                    }
                }
                d[pos+1]=nums[i];
            }
        }
        return len;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

42. 最长连续递增序列

例题674：
给定一个未经排序的整数数组，找到最长且 连续递增的子序列，并返回该序列的长度。

连续递增的子序列 可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], …, nums[r - 1], nums[r]] 就是连续递增子序列。

遍历数组，碰到连续递增的更新结果，不连续递增将中间态置为1从头开始。

class Solution {
    public int findLengthOfLCIS(int[] nums) {
        int res=1;
        int t=1;
        int n=nums.length;
        if(n==1) return 1;
        if(n==0) return 0;
        for(int i=1;i<n;i++){
            if(nums[i]>nums[i-1]){
                t++;
                res=Math.max(t,res);
            }
            else{
                t=1;
            }
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

43. 最长重复子数组

例题718：
给两个整数数组 nums1 和 nums2 ，返回 两个数组中 公共的 、长度最长的子数组的长度 。

如果用暴力法，需要两层for循环找到开始比较的位置，再用一层for进行比较。

动态规划

1. 确定dp数组及下标含义
   dp[i][j]表示下标i-1的数组A与下标j-1的数组B的最长公共重复子数组长度。
2. 确定递推公式
   dp[i][j]由dp[i-1][j-1]决定，如果nums1[i]==nums2[j]，那么dp[i][j]=dp[i-1][j-1]+1.
3. 初始化
   由递推公式可以知道，i和j都从1开始遍历，那么i=0，j=0都是0.
4. 遍历方向
   两层for循环遍历两个数组

代码如下：

class Solution {
    public int findLength(int[] nums1, int[] nums2) {
        int n1=nums1.length;
        int n2=nums2.length;
        int[][] dp=new int[n1+1][n2+1];
        int res=0;
        for(int i=0;i<n1;i++){
            dp[i][0]=0;
        }
        for(int j=0;j<n2;j++){
            dp[0][j]=0;
        }
        for(int i=1;i<=n1;i++){
            for(int j=1;j<=n2;j++){
                if(nums2[j-1]==nums1[i-1]){
                    dp[i][j]=dp[i-1][j-1]+1;
                    res=Math.max(res,dp[i][j]);
                }
            }
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

44. 最长公共子序列

例题1143：
给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，“ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

和上一题类似，不过这道题是不连续的子序列，子数组是连续的。唯一不同的就是，连续数组只有两者相等时才会+1，而不连续时，当text1[i-1]!=text2[j-1]时，当前dp[i][j]就由dp[i-1][j]和dp[i][j-1]的最大值决定。

动态规划

1. 确定dp数组及下标含义
   dp[i][j]表示从0到i-1的字符串A和从0到j-1的字符串B的最长公共子序列长度。
2. 确定递推公式
   dp[i][j]由dp[i-1][j-1]决定：
   ① 如果A[i-1]与B[j-1]相同，那么dp[i][j]=dp[i-1][j-1]+1
   ② 如果A[i-1]与B[j-1]不相同，那么就要看A[i-1]与B[j-2]的最长子序列长度，与A[i-2]与B[i-1]的最长长度的最大值。dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1])
3. 初始化
   i=0,j=0都为0
4. 遍历方向
   依次遍历两个字符串

代码如下：

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int n1=text1.length();
        int res=0;
        int n2=text2.length();
        int[][] dp=new int[n1+1][n2+1];
        for(int i=0;i<=n1;i++){
            dp[i][0]=0;
        }
        for(int j=0;j<=n2;j++){
            dp[0][j]=0;
        }
        for(int i=1;i<=n1;i++){
            for(int j=1;j<=n2;j++){
                if(text1.charAt(i-1)==text2.charAt(j-1)){
                    dp[i][j]=dp[i-1][j-1]+1;
                }
                else{
                    dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
                }
                res=Math.max(res,dp[i][j]);
            }
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

45. 不相交的线

例题1035：
在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。

现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足满足：

nums1[i] == nums2[j]
且绘制的直线不与任何其他连线（非水平线）相交。
请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。

以这种方法绘制线条，并返回可以绘制的最大连线数。

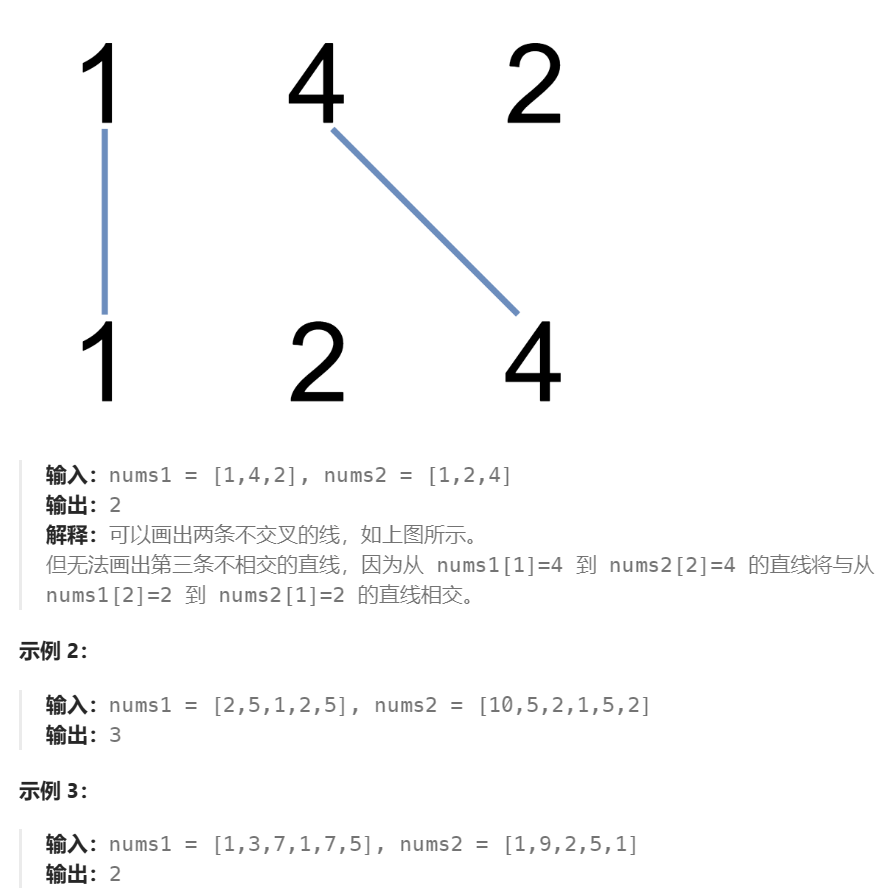
这道题与上道题类似，找最长公共子序列。子序列中相对位置不改变，如果有相交的线相对位置改变就不是最长公共子序列。
难点就是把题目抽象为最长公共子序列的问题！

class Solution {
    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        int n1=nums1.length;
        int res=0;
        int n2=nums2.length;
        int[][] dp=new int[n1+1][n2+1];
        for(int i=0;i<=n1;i++){
            dp[i][0]=0;
        }
        for(int j=0;j<=n2;j++){
            dp[0][j]=0;
        }
        for(int i=1;i<=n1;i++){
            for(int j=1;j<=n2;j++){
                if(nums1[i-1]==nums2[j-1]){
                    dp[i][j]=dp[i-1][j-1]+1;
                }
                else{
                    dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
                }
                res=Math.max(res,dp[i][j]);
            }
        }
        return res;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

46. 最长子序和

例题53：
给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

class Solution {
    public int maxSubArray(int[] nums) {
        int res=nums[0];
        int t=nums[0];
        for(int i=1;i<nums.length;i++){
            t=Math.max(nums[i],t+nums[i]);
            res=Math.max(res,t);
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11

动态规划

1. 确定dp数组及下标含义
   dp[i]表示从0到第i-1个元素的最大和。
2. 确定递推公式
   dp[i]由dp[i-1]决定
   dp[i]=Math.max(nums[i],nums[i]+dp[i-1])
3. 初始化
   dp[0]=nums[0]
4. 遍历方向
   从前往后

代码如下：

class Solution {
    public int maxSubArray(int[] nums) {
if (nums.length == 0) {
            return 0;
        }
        int res = nums[0];
        int[] dp = new int[nums.length];
        dp[0] = nums[0];
        for (int i = 1; i < nums.length; i++) {
            dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
            res = res > dp[i] ? res : dp[i];
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15