- 1pytorch实现GoogLeNet_googlenet pytorch
- 2Selenium模拟浏览器访问_selenium伪装浏览器
- 3【Java中间件】RocketMQ_java rocketmq
- 4Git 下载代码提示SSL certificate problem: self signed certificate in certificate chain解决方法_git pull报错 self signed certificate
- 5GitHub Desktop图文教程_github desktop 教程
- 6软件外包项目的管理
- 7宝塔搭建站点(无域名版本、解决80端口占用)_宝塔没有域名直接做网站怎么弄
- 8基于MATLAB的遗传算法优化卡车和两架无人机的配送路径规划_卡车无人机协同配送代码
- 9C++ STL之copy函数_c++ std::copy
- 10网络是怎样连接的-小笔记
【视频讲解】偏最小二乘结构方程模型PLS-SEM分析白茶产业数字化对共同富裕的影响|附代码数据...
赞
踩
全文链接:https://tecdat.cn/?p=36314
分析师:Qiancheng Yu
本文将通过视频讲解,展示如何用偏最小二乘结构方程模型PLS-SEM分析白茶产业数字化对共同富裕的影响,并结合Python用偏最小二乘回归Partial Least Squares,PLS分析桃子近红外光谱数据可视化实例和R语言结构方程模型SEM、路径分析房价和犯罪率数据、预测智力影响的代码数据,为读者提供一套完整的实践数据分析流程(点击文末“阅读原文”获取完整代码数据)。
视频
案例背景
在当代中国,共同富裕已成为社会经济发展的重要目标。本案例旨在深入探讨产业数字化转型对共同富裕的推动作用,特别是以安吉白茶产业为例,详细分析白茶产业数字化建设对共同富裕的实际影响,并预测其未来作用趋势。安吉白茶产业以其独特的地理优势和文化底蕴,在数字化浪潮中展现出巨大的发展潜力,成为研究产业数字化与共同富裕关系的典型案例。
研究方法
为了全面、准确地评估安吉白茶产业数字化对共同富裕的影响,本案例采用了偏最小二乘结构方程模型(PLS-SEM)作为实证分析方法。PLS-SEM是一种结合了主成分分析、典型相关分析和普通最小二乘法的多元统计方法,能够有效处理复杂的因果关系和潜在变量。
数据来源
本案例的数据主要来源于2022年8月份在安吉当地进行的问卷调查。通过精心设计的问卷,我们收集了关于安吉白茶产业数字化程度、农户收入、就业情况等方面的数据,为后续的模型分析提供了坚实的基础。
偏最小二乘结构方程模型(PLS-SEM)介绍
PLS-SEM的核心在于通过提取主成分和典型相关分析来捕捉自变量和因变量之间的复杂关系。具体而言,对于给定的p个因变量Y=(y1,...,yp)T和n个自变量X=(x1,...,xn)T,PLS-SEM首先通过主成分分析提取自变量中的第一主成分T1,并寻找因变量中的第一主成分U,使得T1与U之间的相关关系达到最大。然后,通过拟合Y与T1的回归方程来评估自变量对因变量的影响。如果拟合精度达到满意程度,则迭代结束;否则,将继续提取第二主成分并拟合新的回归方程,直至满足预设的停止准则。
通过这种方法,PLS-SEM能够有效地揭示安吉白茶产业数字化与共同富裕之间的潜在关系,为政策制定和实践指导提供有力的科学依据。
结构方程模型
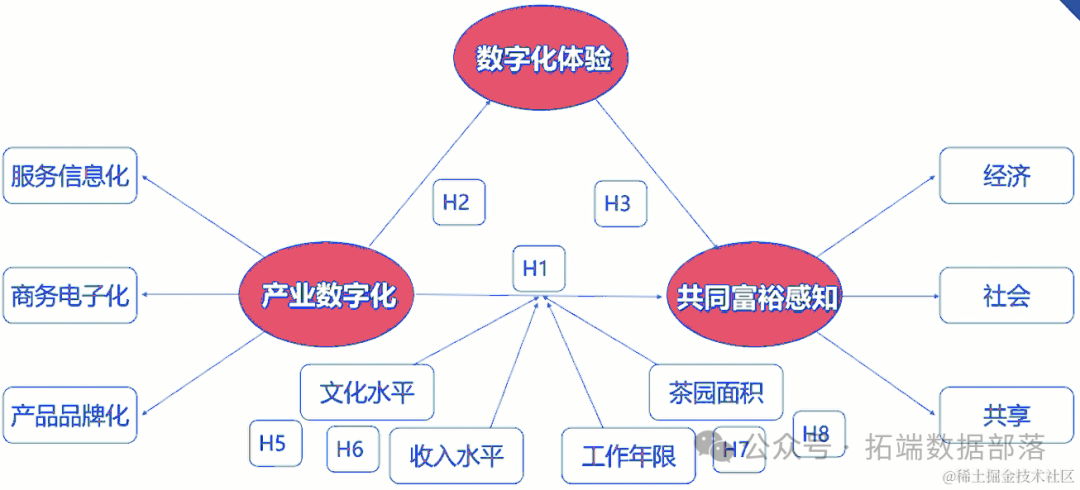
外模型结果显示
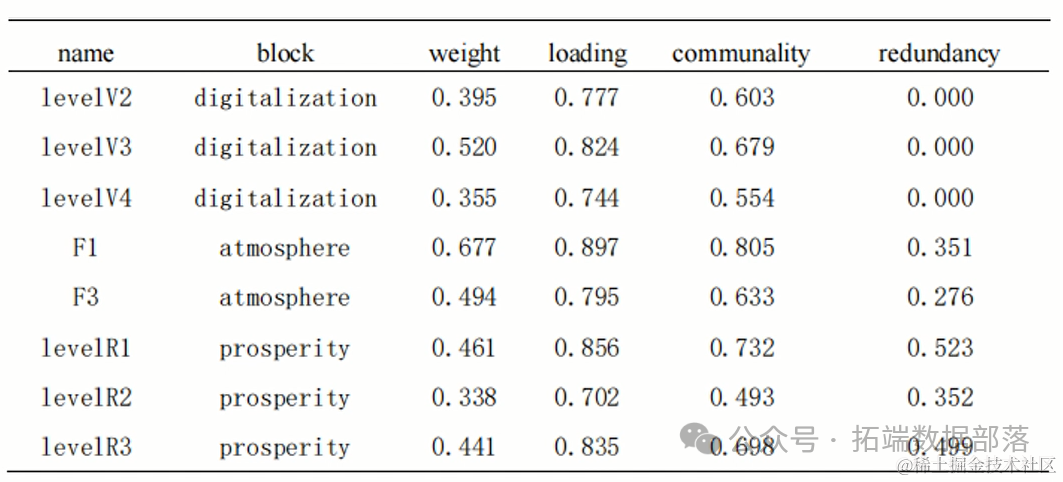
内模型结果显示
具体而言,数字化水平的因素负荷量范围为0.744至0.824,表明数字化因素在模型中对共同富裕具有显著且重要的影响。这一结果反映了数字化技术在安吉白茶产业中的应用程度与其对共同富裕的推动作用之间存在较强的关联性。
同时,氛围感知的因素负荷量在0.795至0.897之间,显示了当地对产业数字化氛围的感知与共同富裕水平之间的紧密联系。这一结果可能表明,当地对产业数字化转型的积极态度和氛围对共同富裕的实现具有积极的推动作用。
共同富裕水平的因素负荷量范围在0.702至0.856之间,这一结果表明共同富裕水平在模型中是一个稳定且有效的变量,其变化受到数字化水平和氛围感知等因素的显著影响。
值得注意的是,上述因素负荷量的标准值均来源于专家的参考文献,这进一步验证了本研究的科学性和可靠性。这些结果表明,安吉白茶产业的数字化转型对共同富裕的促进作用得到了有效验证,同时也为其他产业的数字化转型提供了有益的参考。
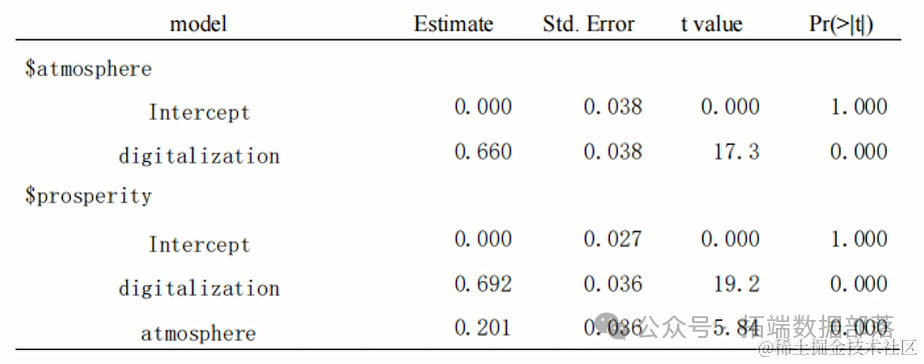
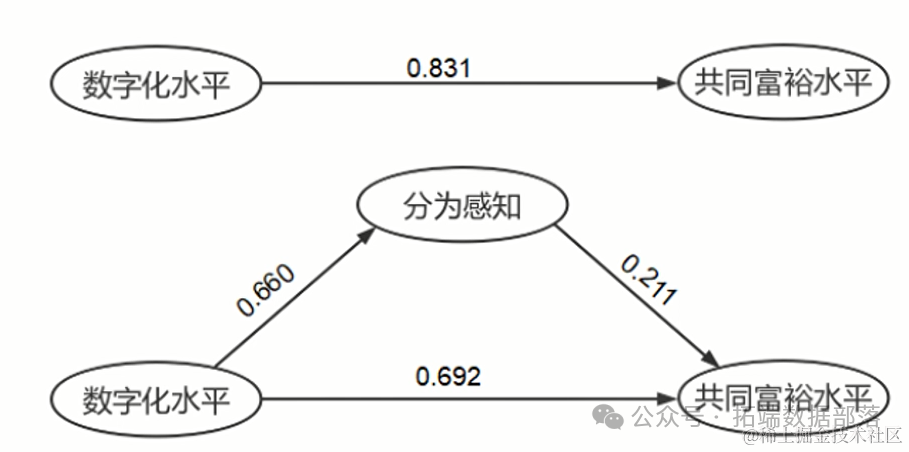
数字化水平对共同富裕产生影响的系数值为0.831,p值远小于0.001,且置信区间(0.797,0.860)不包含o,表明数字化对共同富裕水平的影响是正向显著的。其解释能力R2只有0.69,表明其单项度模型的解释力一般。
当结构模型中加入了氛围感知变量后,共同富裕水平的被解释R2值增加到0.774,表明模型对于共同富裕的解释能力在中等至较大之间,模型解释力较好其次,数字化水平对于氛围感知的回归系数为0.703,p 值远小于0.001,且置信区间不包含0,这表明数字化水平对氛围感知具有显著的正向影响。
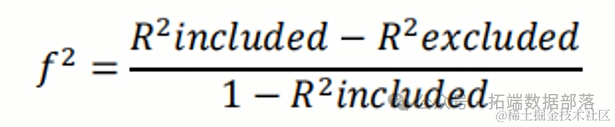
计算中介效应
在结构方程模型中,中介效应通常用于评估一个变量(中介变量)在解释两个其他变量(自变量和因变量)之间关系时的作用。在您给出的案例中,氛围感知变量被视为中介变量,它影响了数字化水平和共同富裕水平之间的关系。
中介效应的计算通常涉及以下步骤:
计算自变量(数字化水平)对中介变量(氛围感知)的影响系数(记作a)。
计算中介变量(氛围感知)对因变量(共同富裕水平)的影响系数(记作b),同时考虑自变量(数字化水平)的影响(记作c')。
计算自变量(数字化水平)直接对因变量(共同富裕水平)的影响系数(记作c)。
然后,中介效应的大小可以通过以下公式计算:
中介效应 = a * b
我们没有直接得到a和b的值,而是得到了氛围感知变量纳入模型前后,共同富裕水平变量的解释力度的变化。不过,我们可以根据这个变化来估算中介效应。
当氛围感知变量纳入模型中时,共同富裕水平变量的解释为0.774,而将氛围感知变量剔除在模型外时,共同富裕水平变量的被解释降低为0.69,根据上述公式计算得出,氛围感知中介变量的实际效应值为0.3717。
偏最小二乘的优缺点
优点:
偏最小二乘(PLS)提供了一种多因变量对多自变量的回归建模方法,特别适用于处理变量之间的多重共线性问题。
PLS对样本的分布没有严格要求,因此在非正态分布或小样本情况下也能得到较稳定的结果。
PLS能够同时考虑多个因变量和自变量之间的关系,从而提供更全面的信息。
缺点:
PLS估计不再是因变量的线性函数,其优良特性与非线性估计的特性仍在研究中,这可能使得PLS在某些复杂模型中的解释性受到限制。
PLS的结果可能受到初始变量选择的影响,不同的变量组合可能导致不同的结果。
PLS在处理高维数据时可能会遇到计算复杂性和稳定性方面的问题。
Python用偏最小二乘回归Partial Least Squares,PLS分析桃子近红外光谱数据可视化
PLS,即偏最小二乘(Partial Least Squares),是一种广泛使用的回归技术,用于帮助客户分析近红外光谱数据。如果您对近红外光谱学有所了解,您肯定知道近红外光谱是一种次级方法,需要将近红外数据校准到所要测量的参数的主要参考数据上。这个校准只需在第一次进行。一旦校准完成且稳健,就可以继续使用近红外数据预测感兴趣参数的值。
PCR只是使用通过PCA得到的若干主成分构建的回归模型。显然,这并不是最佳选择,而PLS就是解决这个问题的方法。
在本文中,我将向您展示如何使用Python构建一个简单的PLS回归模型。以下是我们将要做的概述。
展示PLS的基本代码
讨论我们要分析的数据及所需的预处理。我们将使用新鲜桃子水果的近红外光谱,其关联的Brix值与PCR相同。这是我们要校准的量。
我们将使用交叉验证方法构建我们的模型
PLS Python代码
好的,以下是基于Python 3.5.2的运行PLS交叉验证的基本代码。
- # 导入需要的库
- from sklearn.metrics import mean_squared_error, r2_score # 导入均方误差和R2得分指标
- from sklearn.model_selection import cross_val_predict # 导入交叉验证函数
-
-
-
- # 定义PLS对象
- pls = PLSReg......
- nts=5) # 定义保留5个成分的PLS回归模型
-
-
-
- # 拟合数据
- pls.f......
- Y) # 将数据拟合到PLS模型中
-
-
-
- # 交叉验证
- y_cv = cros......
- y, cv=10) # 用10折交叉验证计算模型性能
-
-
-
- # 计算得分
- score = r2_score(y,v) # 计算R2得分
- mse = mean_squa......
- _cv) # 计算均方误差

为了检查我们的校准效果如何,我们使用通常的指标来衡量。我们通过将交叉验证结果y_cv与已知响应进行比较来评估这些指标。为了优化我们的PLS回归参数(例如预处理步骤和成分数量),我们将跟踪这些指标,最常见的是均方差(MSE)。
还有一件事。在实际代码中,各种数组X, y等通常是从电子表格中读取的numpy数组。因此,您可能需要导入numpy(当然),pandas和其他一些库,我们将在下面看到。
这是Python中PLS回归的基本代码块。看一下数据导入和预处理了。
近红外数据导入和预处理
- from sys import stdout
-
- ......
- from sklearn.metrics import mean_squared_error, r2_score
接下来,让我们导入数据,这些数据保存在一个csv文件中。该数据由50个新鲜桃子的近红外光谱组成。每个光谱都有对应的Brix值(响应变量)。最后,每个光谱在1100 nm到2300 nm之间取600个波长点,步长为2 nm。
- data = pd.read_csv('./datavalues.csv')
-
- # 获取参考值
-
- y = data[......
- lues
-
- # 获取光谱
-
- X = data......
- axis=1).values
-
- # 获取波长
-
- wl = np.a......
- 0,2300,2)

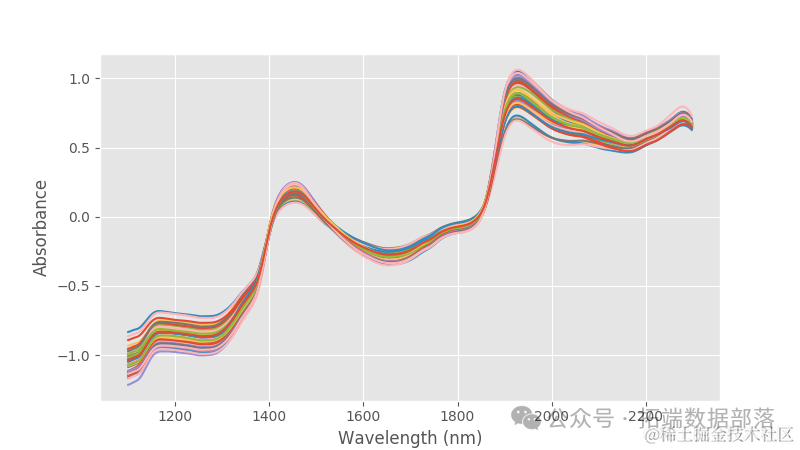
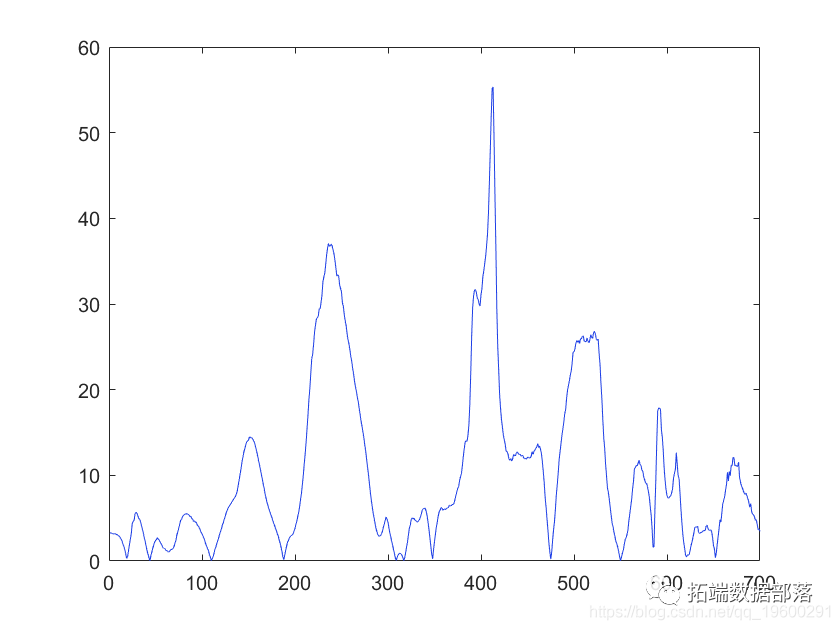
如果需要,数据可以通过主成分分析进行排序,并使用乘法散射校正进行校正,然而,一个简单但有效的去除基线和线性变化的方法是对数据进行二阶导数。让我们这样做并检查结果。
- # 计算二阶导数
-
- X2 = savgol_fi
- ......
- order = 2,deriv=2)
-
-
-
- # 绘制二阶导数图像
-
- plt.figure(fi......
- (8,4.5))
-
- with plt.style.context(('ggplot')):
- ......
-
-
- plt.show()

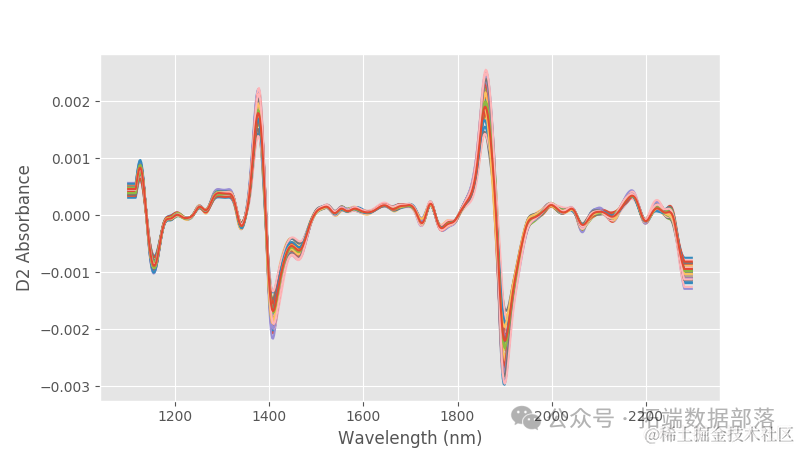
偏移已经消失,数据看起来更加紧密。
点击标题查阅往期内容

Matlab中的偏最小二乘法(PLS)回归模型,离群点检测和变量选择

左右滑动查看更多

01
02

03
04
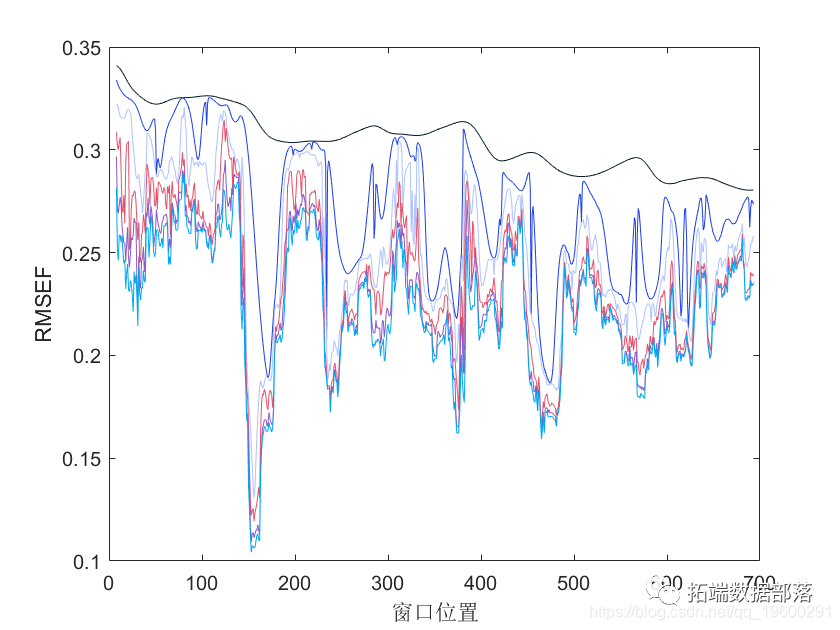
偏最小二乘回归
现在是时候优化偏最小二乘回归了。如上所述,我们想要运行一个具有可变组分数的偏最小二乘回归,并在交叉验证中测试其性能。实际上,我们想要找到最小化均方误差的组件数。让我们为此编写一个函数。
- def optimisls_cv(X, ......
- =True):
-
-
-
- '''运行包括可变组件数量的偏最小二乘回归,最多到n_comp,并计算均方误差'''
-
-
-
- mse = []
- ......
-
- for i in component:
-
- pls = PLSR......
-
-
- # 交叉验证
-
- y_cv = cross_v......
-
-
-
- comp = 100*(i+1)/n_comp
-
- # 在同一行上更新状态的技巧
-
- stdout.write("\r%
- ......
-
- # 计算并打印均方误差最小值的位置
- msemin = np......
- stdout.write("\n")
-
- if plot_components is True:
- ......
-
- plt.title('PLS')
- plt.xlim(left=-1)
-
- plt.show()
-
- # 使用最佳组件数定义PLS对象
- pls_opt = PLSRe......
- # 对整个数据集进行拟合
- pls_opt.......
- t.predict(X)
-
- # 交叉验证
- y_cv = cros......
- cv=10)
-
- # 计算校准和交叉验证的得分
- score_c = r2......
- e(y, y_cv)
-
- # 计算校准和交叉验证的均方误差
- mse_c = mean_......
- y, y_cv)
-
-
- # 绘制回归图和评估指标
- rangey = m......
- - min(y_c)
-
- # 将交叉验证和响应拟合为一条直线
- z = np.poly......
- 'red', edgecolors='k')
- # 绘制最佳拟合线
- ax.plot(np.p......
- , linewidth=1)
- # 绘制理想的1:1线
- ax.plot(y, ......
- idth=1)
-
-
- plt.show()
-
- return

这个函数首先运行了一个循环,通过偏最小二乘回归的组件数计算预测的均方误差。其次,它找到最小化均方误差的组件数,并使用该值再次运行偏最小二乘回归。在第二次计算中,计算了一堆指标并将其打印出来。
让我们通过将最大组件数设置为40来运行此函数。
- optimise......
- , plot_components=True)
第一个图表是均方误差作为组件数的函数。建议最小化均方误差的组件数在该图中突出显示。
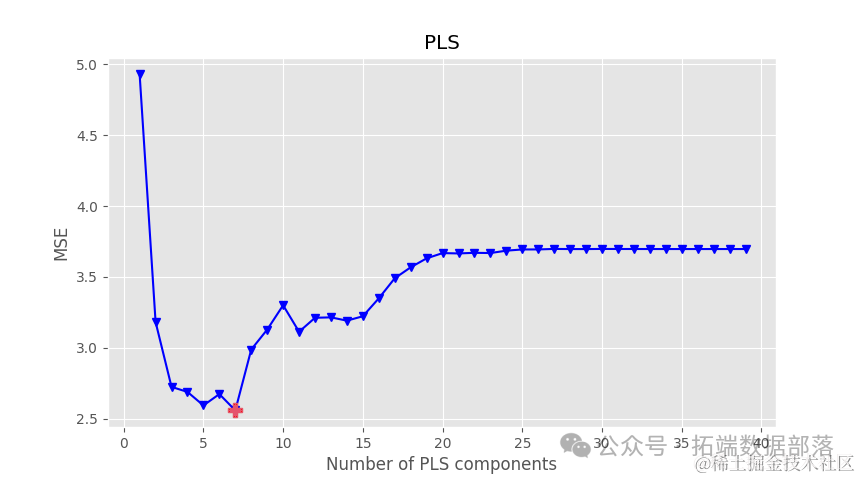
第二个图表是实际的回归图,包括预测指标。
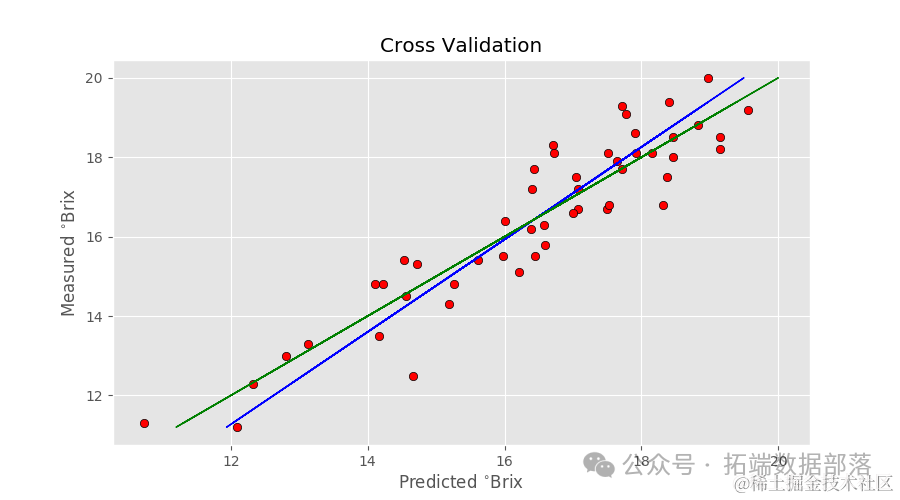
同时,在屏幕上会打印出以下信息。
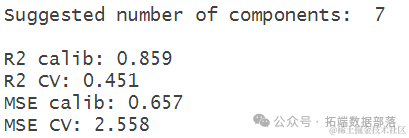
该模型在校准数据上似乎表现良好,但在验证集上的表现则不尽如人意。这是机器学习中所谓的过拟合的经典例子。
R语言结构方程模型SEM、路径分析房价和犯罪率数据、预测智力影响因素可视化2案例
1 简介
在本文,我们将考虑观察/显示所有变量的模型,以及具有潜在变量的模型。第一种有时称为“路径分析”,而后者有时称为“测量模型”。
2 进行简单的多元回归
SEM 在很大程度上是回归的多元扩展,我们可以在其中一次检查许多预测变量和结果。SEM 还提供了检查潜在结构(即未观察到某些变量的地方)的创新。更具体地说,“结构方程”的概念是指我们有不止一个方程表示协方差结构模型,其中我们(通常)有多个标准变量和多个预测变量。
让我们从简单的演示开始,即 SEM 中的路径模型可以概括简单的单预测变量-单结果回归。我们将检查人口普查中的房价数据,以回顾相关和回归中的重要概念。这是一个很好的回归数据集,因为有许多相互依赖的变量:犯罪,污染物,财产的年龄,等等。
这是上面的单预测回归,作为路径模型运行 :
- #示例数据集,包括按人口普查区划分的房屋价格
-
- Bsnml <- otnou %>% dplyr::select(
- cmv, #住宅的中位数价值,以千计
- crm, #城镇人均犯罪率
- nx, #一氧化氮浓度
- lsa, #地位较低的人的比例
- rd #靠近放射状的高速公路
- ) %>% mutate
- summary

为了比较,输出 lm()
summary(lm
回归系数是相同的(好!)。有一点需要注意的是,我们在输出中没有截距。这突出了一个重要的区别,基本的SEM经常关注数据的协方差结构。我们也可以包括均值,但通常只有当它与我们的科学问题有关时才会包括。例如,男性和女性在抑郁症潜在因素的平均水平上是否有差异?
2.1 平均结构
在这种情况下,我们可以要求在模型中包含平均值(截距) mean=TRUE:
summary(lvt)
2.2 模型参数详情
"参数 "表提供了模型中哪些参数是必须被估计,以及用户在模型语法中要求哪些参数的重要摘要。
Table(mv)
在这里,'user' 指的是我们在语法中明确请求的参数,'free' 列的非零值表示模型自由估计的参数。
请注意,我们也可以得到标准化的估计值 。这是 SEM 中更复杂的主题,因为我们可以仅针对潜在变量(std.lv)或观察变量和潜在变量(std.all)进行标准化。后者通常是 SEM 论文中作为标准化估计报告的内容。
2.3 标准化估计
stdln(v, type)
3 住房数据的路径分析
让我们看一些更有趣的东西。如果我们认为一氧化氮 ( nox) 水平也可以预测房价和犯罪率,那会怎样?我们可以将其添加为标准多元回归中的预测变量。
此外,我们假设房屋靠近大型高速公路(rad)预测一氧化氮的浓度,从而预测较低的房价?
模型语法可以指定为:
sem(ln2, data=toSll)模型看起来像这样
Paths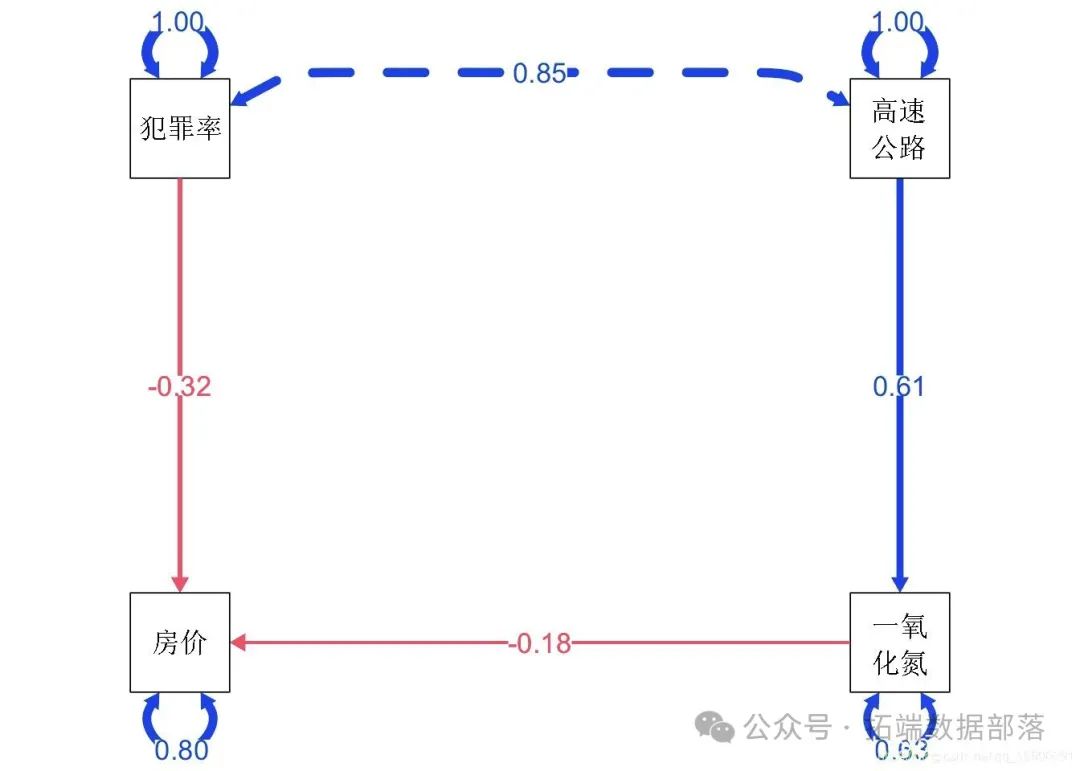
这是文本输出:
summary
需要注意的几点:
请注意警告:“一些观察到的差异(至少)是其他差异的 1000 倍。”
我们的假设似乎都得到了支持。
模型卡方非常显着,表明全局模型拟合不佳。
3.1 调整
当模型中变量的方差显着不同(数量级)时,参数估计可能会遇到困难。鉴于上述警告,让我们来看看。
Table(lv2)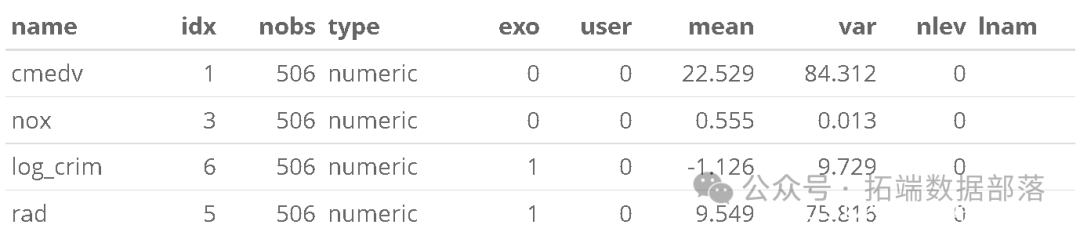
看起来nox的比例要比其他预测因素小得多,可能是因为它的单位是千万分之一!我们可以通过乘以常数来重新调整变量的比例。在这种情况下,我们可以通过乘以一个常数来重新划分变量的尺度。这对模型的拟合或解释没有影响--我们只需要回忆一下新单位代表什么。另外,如果重要的话,你可以随时从参数估计中除掉常数来恢复原来的单位。
- Bonl <- BoSal %>% mutate
- summary(lv2)

3.2 模型拟合指数
您可以在模型摘要输出中使用更详细的全局拟合指数。
summary(fit.me=TRUE)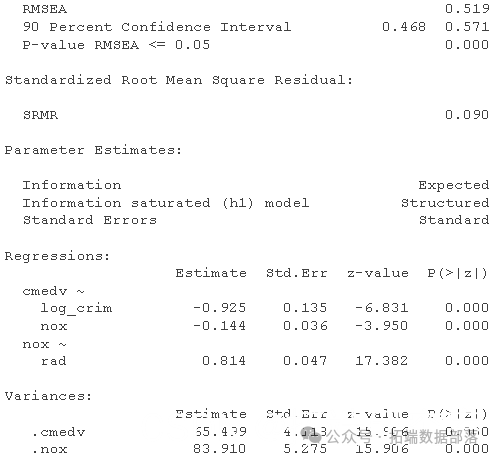
您还可以使用以下方法获取适合的度量(包括其他统计信息)


这些看起来很差:CFI < .95(甚至远低于 0.9),而 RMSEA 远高于我们认为“还可以”的 0.08 水平。
3.3 模型诊断
这表明需要更详细地检查拟合。首先,我们可以查看模型隐含和观察到的协方差矩阵之间的不匹配。
从概念上讲,结构方程建模 (SEM) 的目标是测试变量间协方差的理论动机模型是否提供了数据的良好近似。
更具体地说,我们试图测试一个解析模型(由测量和/或结构成分组成)对观察到的协方差矩阵的再现程度。从形式上看,我们正在寻求建立一个模型,其模型隐含的协方差矩阵接近于样本(观测)协方差矩阵。
SXX≈Σ (θ ^)
我们可以从中获得这些信息, 进一步诊断模型不匹配。
首先,模型隐含的协方差矩阵:
fitted
我们也许可以用相关(标准化)单位更容易地解释这一点。也就是说,变量之间的模型隐含相关性是什么?可以访问许多模型详细信息,包括:

这与观察到的相关性相比如何?
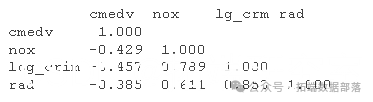
特别是,获得双变量关联的不匹配。在这里,我们要求相关单位中的残差,这比处理未标准化的协方差更直观。请注意,这是上面观察到的模型隐含矩阵的减法。大的正值表明模型低估了相关性;大的负值表明相关性的过度预测。通常值 |r>.1|值得仔细考虑。

因此,该模型显着低估了 nox 和 crim之间的 关联 。
我们也可以将问题可视化:
plot_matix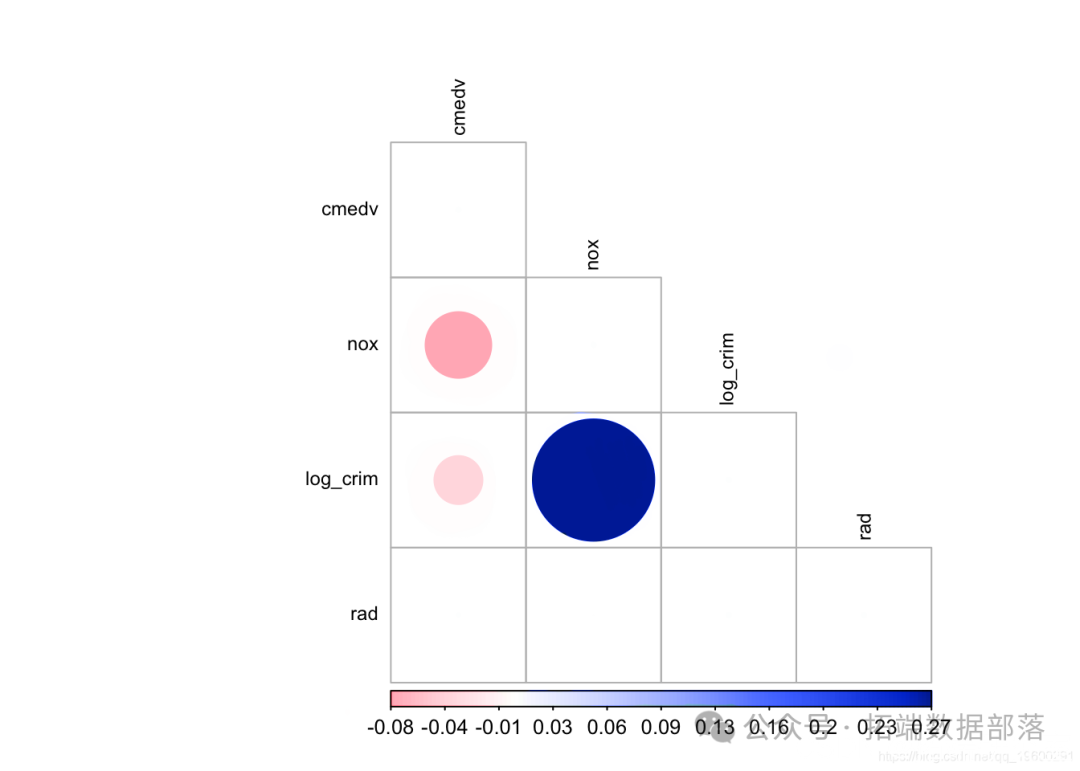
3.4 修改指数
让我们看一下修改索引,看看我们是否可以通过释放一个或多个路径来修复不匹配,特别是nox 和 log_crim之间的 关系 。
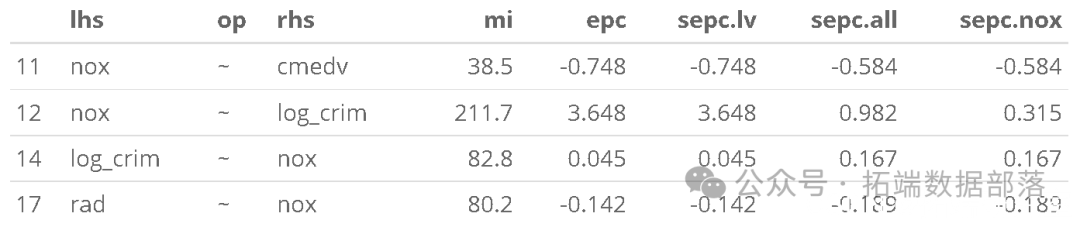
在这里,我们看到如果我们允许 log_crim 预测 ,模型拟合会大大提高nox。这是否具有理论上的意义是另一回事(而且可能更重要)。出于演示目的,让我们接受需要自由估计这条路径。
- #我们可以使用添加参数来添加一个路径,同时保持所有其他模型元素不变
- ma3 <- update
- summary

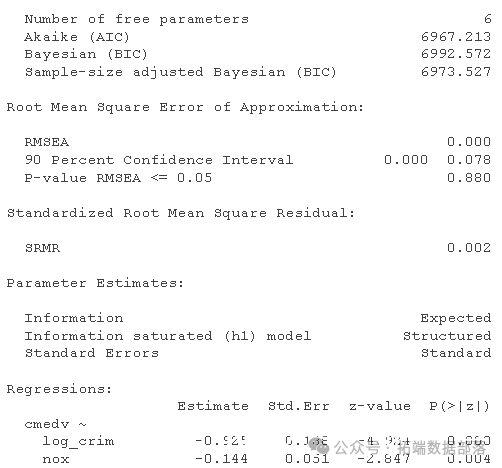
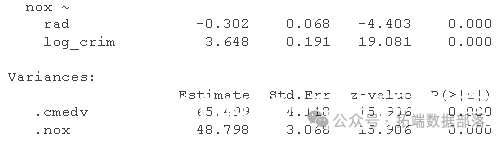
这在拟合方面看起来好多了。 犯罪与我们之前错过的氮氧化物水平之间存在强烈的正相关关系。从概念上讲,这表明犯罪与房价之间的关系部分是由犯罪对污染物水平的影响所调节的。相比之下,靠近高速公路对房价的影响似乎完全由污染物水平调节(正如这条路径没有大的修正指数所示)。
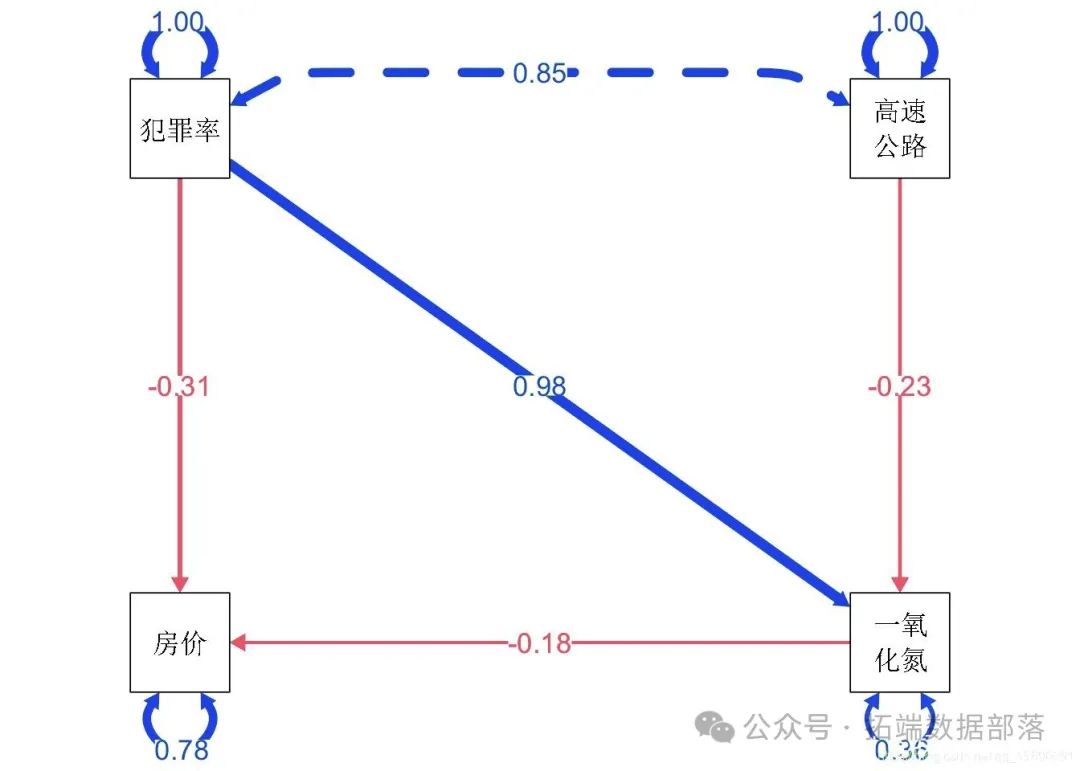
4 检验调解
如果支持上述模型并且我们对测试中介特别感兴趣,我们通常希望 1)专门检验间接效应,以及 2)使用一种方法对提供可信 p值的中介效应进行显着性检验。正如前段时间所指出的(例如,MacKinnon 等人,2007 年),在 SEM 框架中对中介的适当检验是基于 构成中介的成分路径的乘积。 在这里,我们在两个中介链中只有两条路径:
radlog_crim→nox→cmedv→nox→cmedvrad→nox→cmedvlog_crim→nox→cmedv
为了具体测试这些,我们需要在 模型中定义新参数,这些参数是各个路径的产物。这可以使用 =: 运算符('定义为')来完成。请注意,这确实会改变模型中自由参数的数量,因为这些只是现有参数的乘积。为了看哪个估计要相乘,我们必须通过将变量预乘以任意标签来使用“参数标签”。在这里,我将“a1”和“a2”用于 X -> M 路径,将“b1”用于 M -> Y 路径。
- i_1 := a1*b1
- i_2 := a2*b1
- '
- summary(mv4)
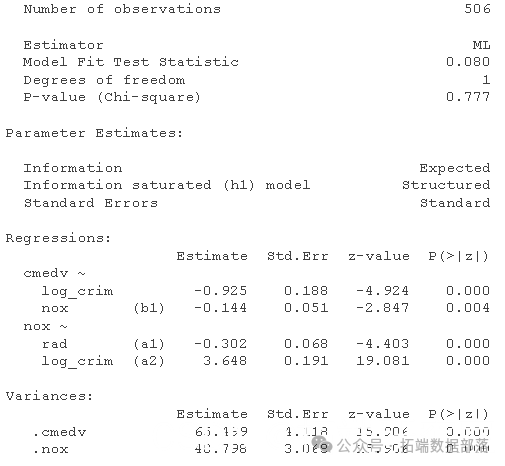

这看起来很有希望,但正如我上面提到的,这种用于测试中介的“delta 方法”众所周知是有问题的,因为间接路径乘积项的抽样分布不正常。Bootstrapping 是解决这种问题的一种常见解决方法,它不会对感兴趣系数的分布(即两个中介路径的采样分布)做出强有力的假设。我们可以使用参数来实现这一点 se = "bootstrap"。默认情况下,这将使用 1000 个非参数引导样本重新估计参数估计的标准误差。您可以使用bootstrap 参数更改引导样本的数量
summary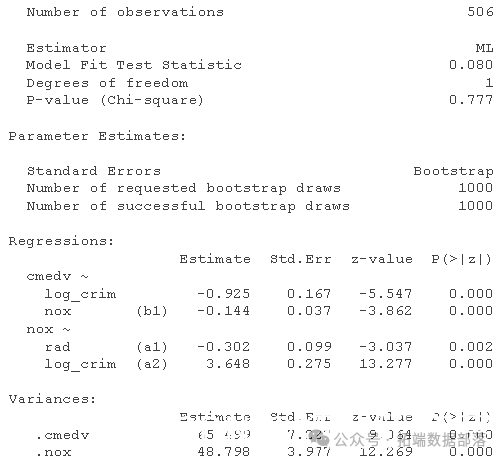

正如我们所怀疑的,这两种间接途径都很重要,表明了调节的证据。
5 带有潜在变量的 SEM
当我们对测试有潜变量的模型感兴趣时,怎么办?通常,这将是一个 "反映性潜变量 "模型,我们认为一个假定的潜变量是由几个(通常是3个以上)显性指标来衡量的。这样的变量通常被称为 "因子 "或 "潜在特质"。在SEM世界中,确认性因子分析是最常见的反映性潜变量模型。
这样的模型中使用=~操作符('测量的')来指定。
让我们以 衡量智力为例,其中有 9 个项目可以衡量智力的不同方面:视觉、文本和速度。观察到的变量是 x1-x9。
这是一个“经典”数据集,用于许多关于结构方程建模 (SEM) 的论文和书籍,包括一些商业 SEM 软件包的手册。数据包括来自两所不同学校的七年级和八年级儿童的心理能力测试成绩。在我们的数据集版本中,仅包含原始 26 个测试中的 9 个。通常针对这 9 个变量提出的 CFA 模型由三个潜在变量(或因子)组成,每个潜在变量具有三个指标:
由 3 个变量测量的 视觉 因子
x1:x2和x3由 3 个变量测量的 文本 因子
x4:x5和x6由 3 个变量测量的 速度 因子
x7:x8和x9
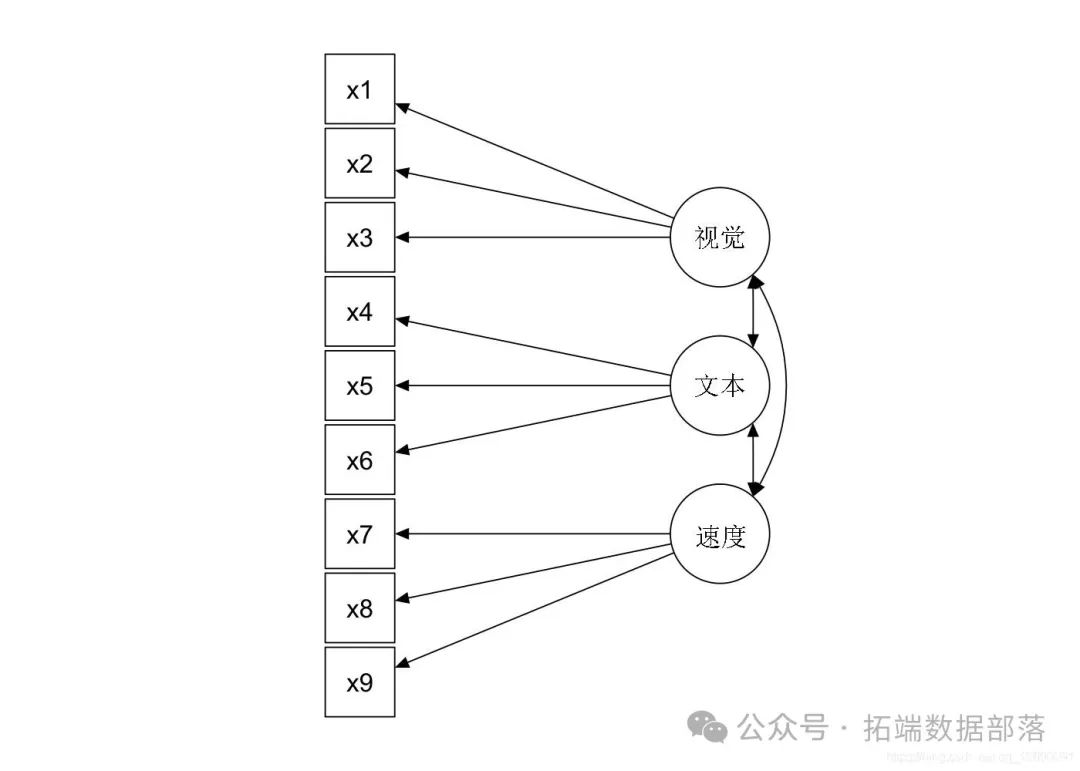
一个 3 因素 CFA 示例
5.1 指定因子模型
指定此模型的相应 语法如下:
- visual =~ x1 + x2 + x3
- textual =~ x4 + x5 + x6
- speed =~ x7 + x8 + x9
在此示例中,模型语法仅包含三个“潜在变量定义”。
5.2 典型 CFA 输出
默认情况下,第一个指标具有 1 的固定负载以缩放基础因子(“单位负载标识”)。让我们来看看:
summary
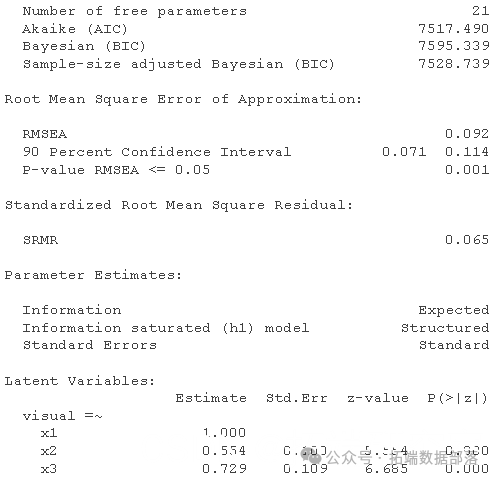
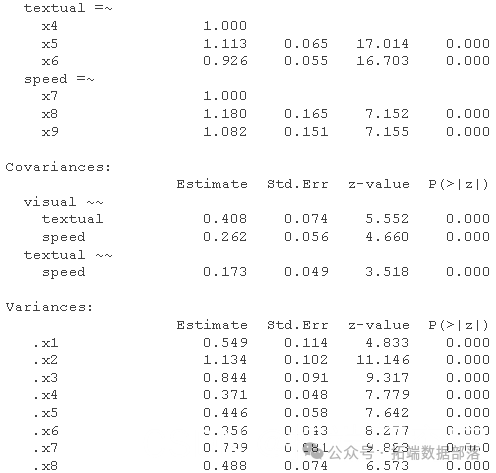

5.3 CFA 的修正指数
modification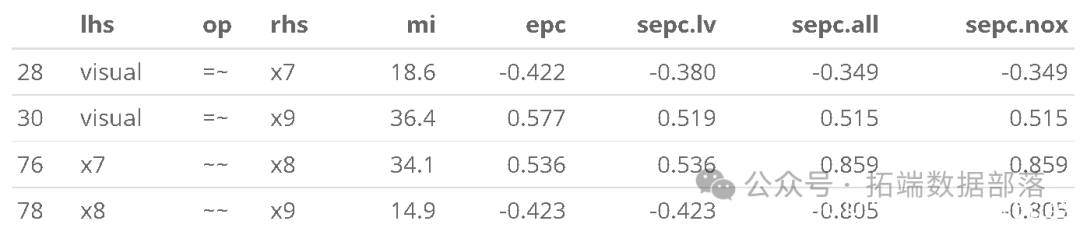
修正指数表明 x9 可能会加载 visual 因子,或者 x7 可能 x9 具有唯一的残差相关性。这又是一个理论上的问题,但我们可以测试修改后的模型以进行演示。我们使用 ~~ 运算符来指定模型中的(残差)方差或协方差项。
summary(fit2, fit.meas)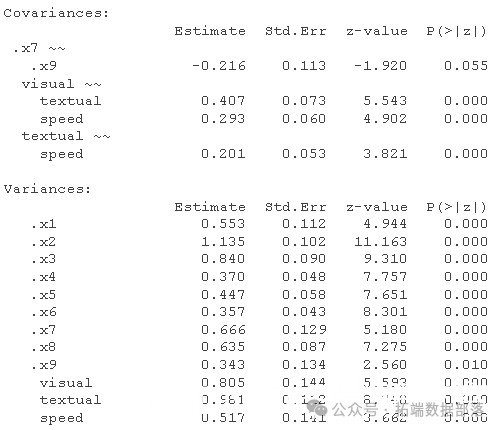
仍然不是很好。我们可以重新检查修改指数
modificatio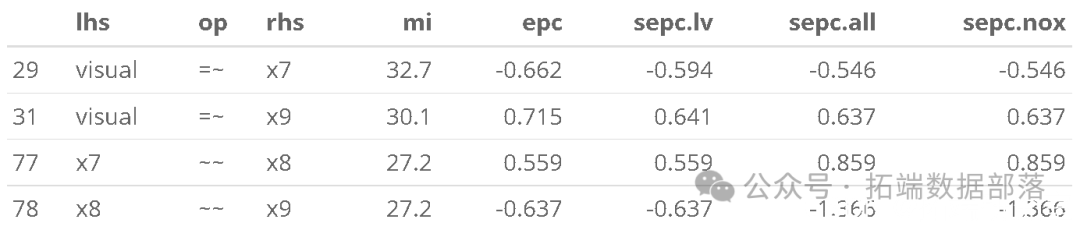
现在是时候咨询你关于潜在结构应该是什么的预测或理论了。这是一个模型构建和模型比较问题,很大程度上超出了本教程的范围。然而,我们至少可以测试这些模型之间的全局拟合差异。这些是嵌套模型(因为 x7 ~~ x9 在更简单的模型中残差协方差为 0),这允许我们使用似然比检验(也称为模型卡方差):
anova
该 anova 函数将使用 LRT 方法测试整体拟合差异。LRT 的自由度是自由参数数量的差异(此处为 1)。
5.4 详细看模型
我们可以查看自由参数在矩阵规范中的位置。自由参数被编号(按顺序),零表示可能的参数,固定为零(即不估计)。
inspect

我们还可以看到矩阵形式的参数估计:
inspect( "est")

5.5 结构模型呢?
上面的 CFA 只包含一个测量模型——一个具有因子之间相关性的三因子模型。如果我们还想看看学校的年级在多大程度上可以预测智力因素(视觉、文本、速度)的水平,该怎么办?
summary( fit.measures=TRUE)

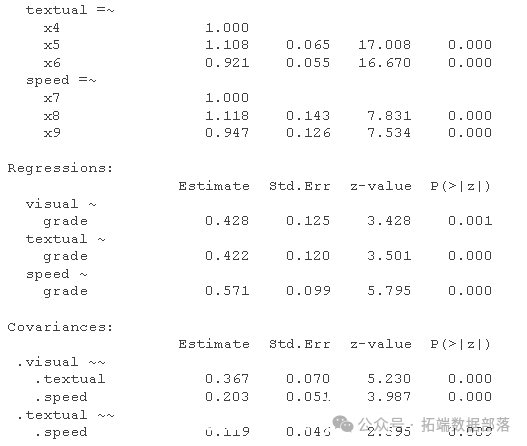
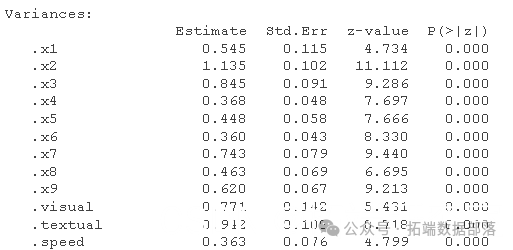
semPath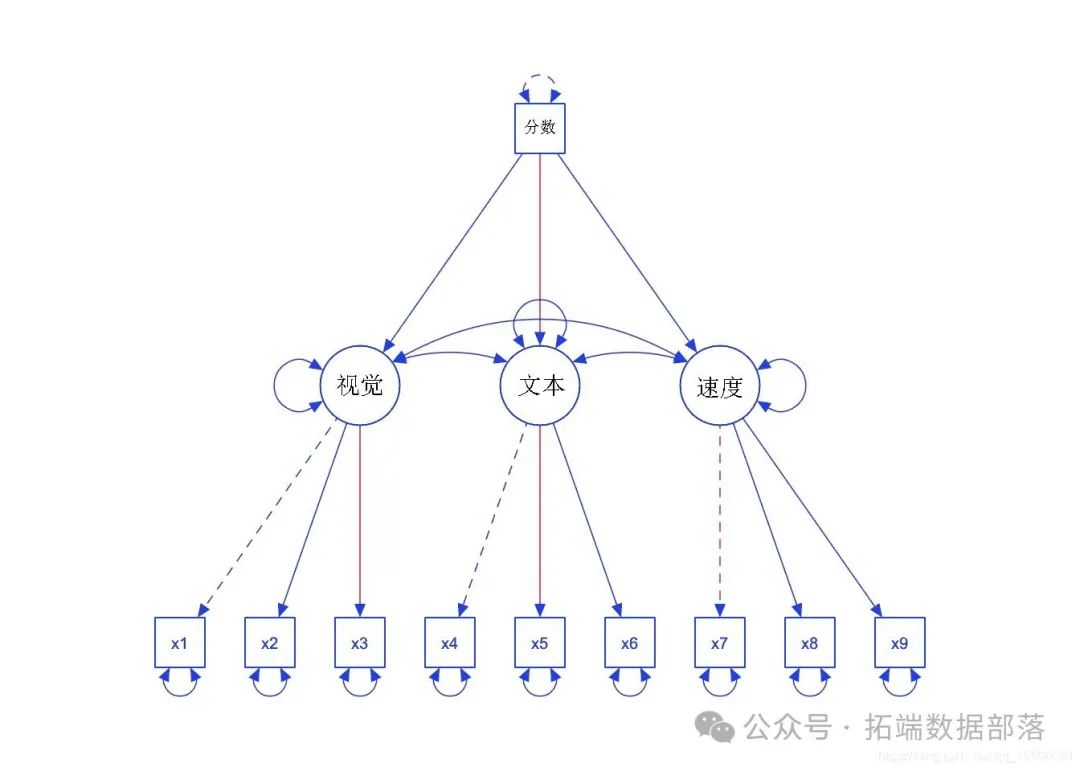
正如人们所预料的那样,高年级的孩子在潜在智力因素上得分更高。
最后,如果我们想在结构模型中使用一般与特定(残差)方差怎么办?为了让它们在相同的参数矩阵中适当地发挥作用,我们为感兴趣的项目残差创建了一个单指标潜在变量。
- x1d =~ 1*x1 #定义干扰因子,将1.0加载到指标上(如RAM的符号)。
- x1 ~~ 0*x1 #指标的零残差(所有加载到干扰因素上)。
-
- #根据标准模型,干扰因素与因子不相关
- x1d ~~ 0*视觉
- x1d ~~ 0*文本
- x1d ~~ 0*速度
-
- #我们现在可以看看X1的具体方差和视觉因素是否能唯一地预测人的年龄
-
- summary(fitne)


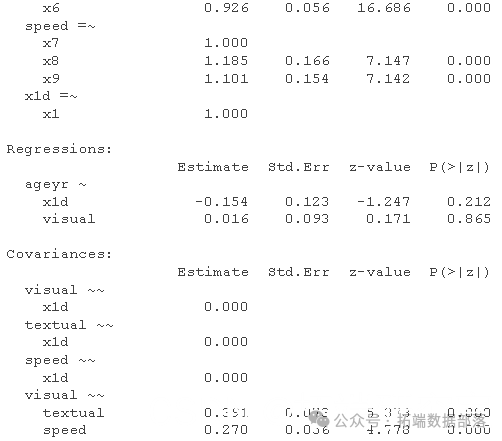
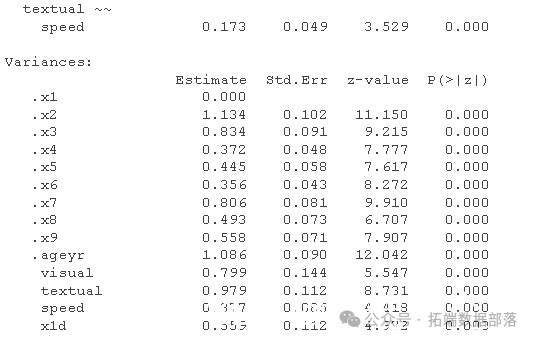
这里没有骰子,但你明白了。
6 分类数据
支持使用阈值结构来正式处理内生的分类数据。这源于这样的观点:一个项目的基本分布是连续的(高斯),但我们的离散化(如二元或多态)在特定的点上降低了这个维度。
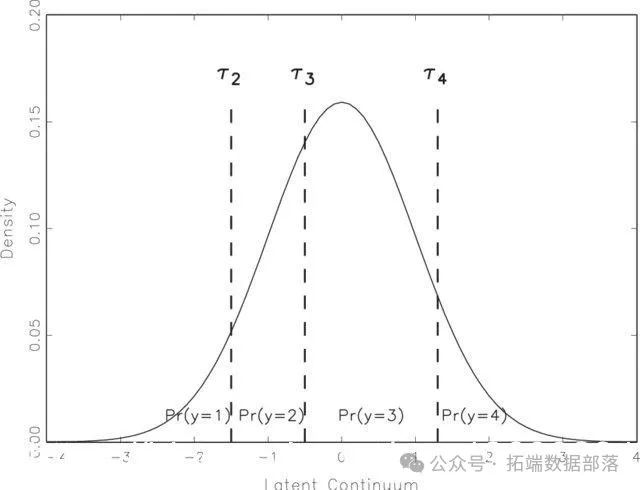
我们有4个级别的变量(1、2、3、4),但只有三个阈值--每个阈值指定两个相邻级别(锚)之间的边界。如果我们有动力来说明这个结构,这些阈值可以被指定为模型中的自由参数。这实质上是在估计ττ参数沿着连续体的落点;它们不需要均匀分布
如果我们对一个项目有5个以上的锚,我们也许可以把它当作连续的,而不会出现重大的错误。请注意,这就是我们在最初的CFA中所做的事情--我们将x1-x9视为正态/连续分布。事实证明,它们是(即不是高度离散的)。
hist(Holz$x1)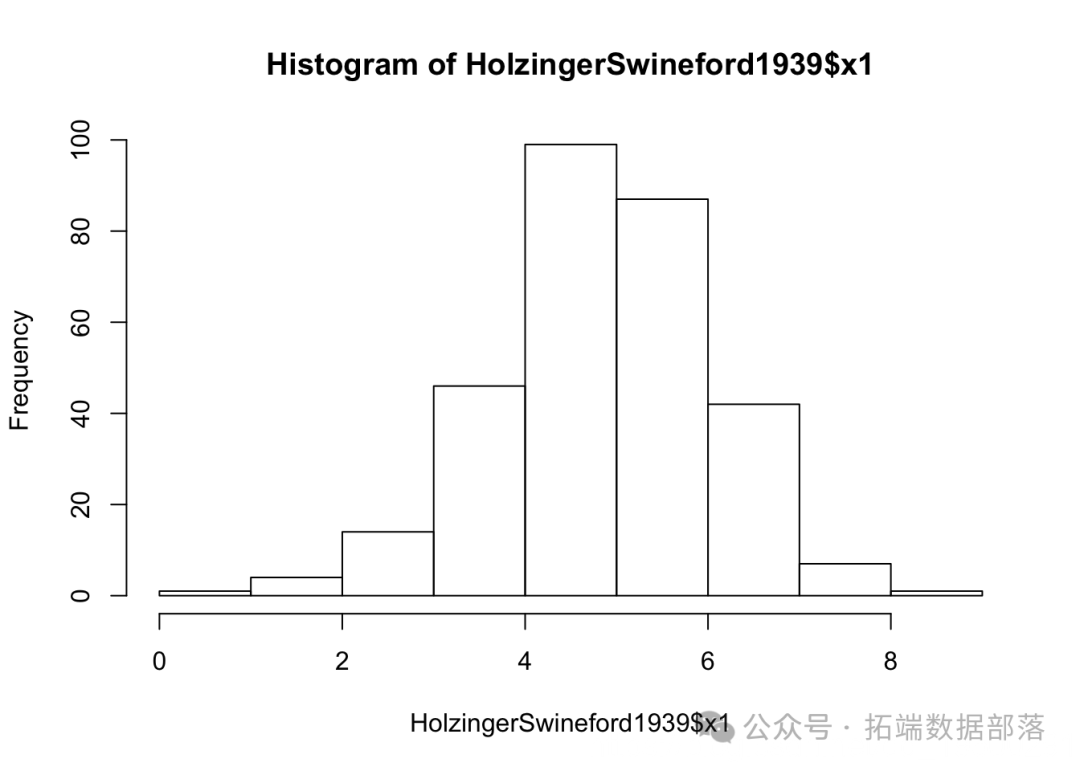
但是,如果我们有具有 2、3 或 4 个值的数据,将变量视为连续变量通常是不合适的,并且可能导致有偏差、不准确的结果。
通常,具有阈值结构的模型是使用“加权最小二乘”(WLS)估计器而不是最大似然(ML;SEM 中的典型估计器)估计的。均值和协方差调整的 WLS(又名“WLSMV”)通常是可行的方法,因为它可以比典型的 WLS 更好地处理多元分布的非正态性。
6.1 CFA分类数据演示
这是一个快速演示——如果我们的每个智力测试项目只有三分法怎么办?
hist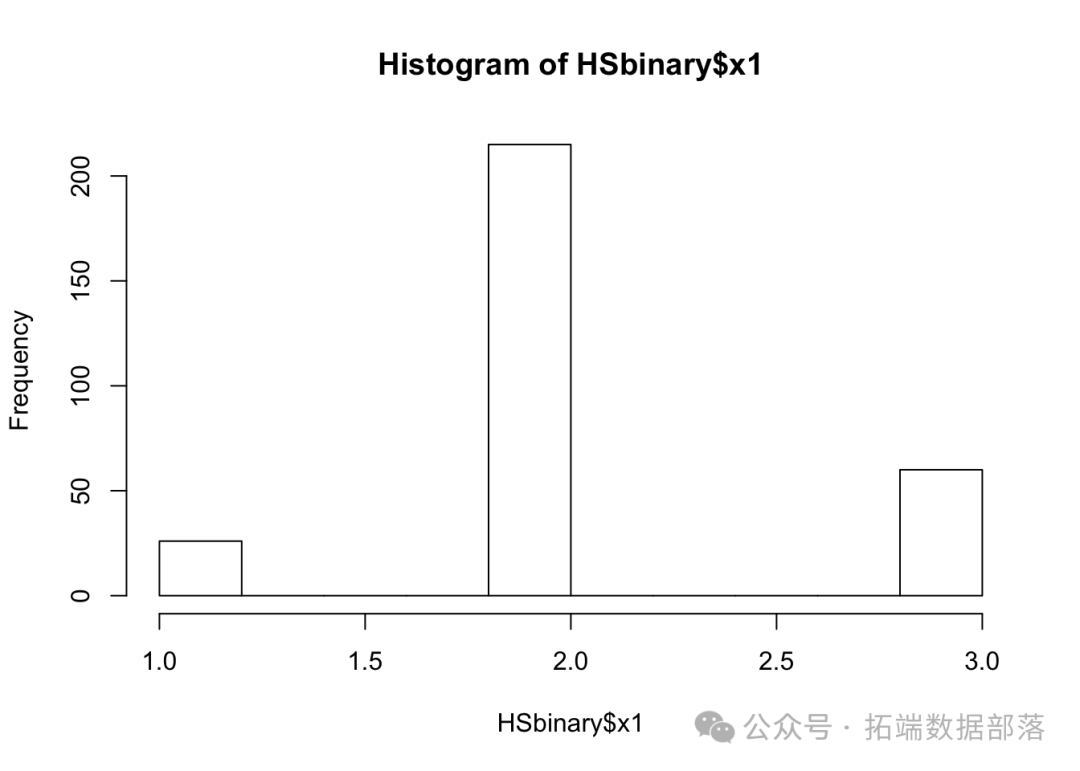
我们用有序参数告诉R哪些项目是有序分类的。
summary(fiat)
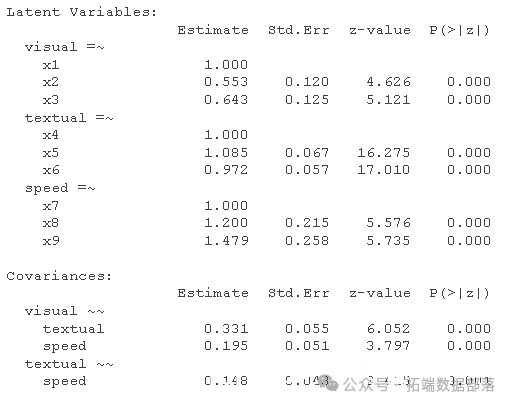

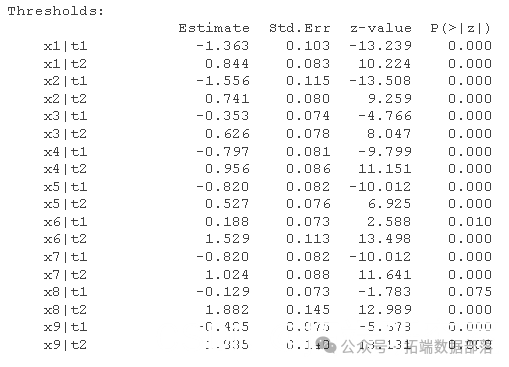
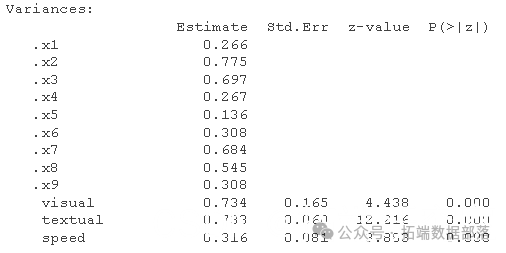
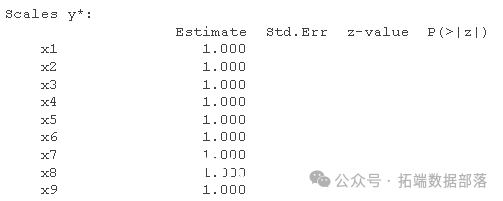
请注意,我们现在对每个项目都有阈值估计,其中较高的数值表示对一个类别和下一个类别之间的边界有较高的估计,而这个潜在的连续体据说是该项目的基础。
7 估计
最后, 可以用许多不同的算法来估计模型中的参数。“ML”是连续数据的默认值,“WLS”是(部分)分类数据的默认值。
这些估计器的'稳健'通常会在整个模型的卡方检验和标准误差的层面上对非正态性(以及潜在的其他东西,如聚类)进行稳健处理,因此,显著性检验。让你的统计数据对非正态性具有鲁棒性通常是一件好事......因此,许多人将使用 "MLR "作为他们对连续数据的首选,而 "WLSMV "则用于分类数据。
可以使用 estimator 参数指定它。
summary(filr, fit.measures=TRUE)
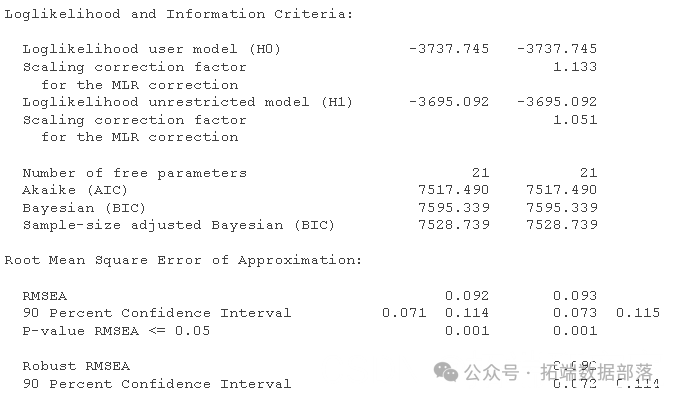
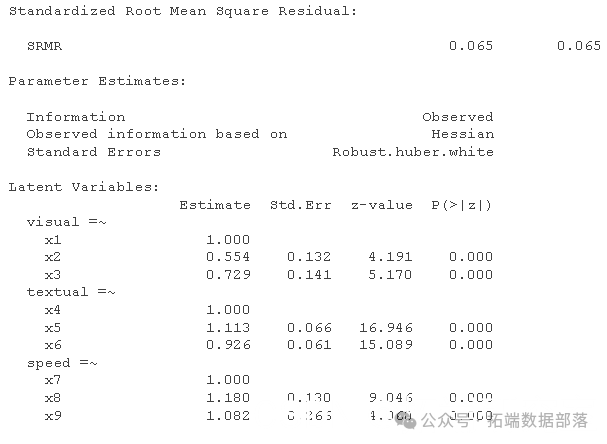
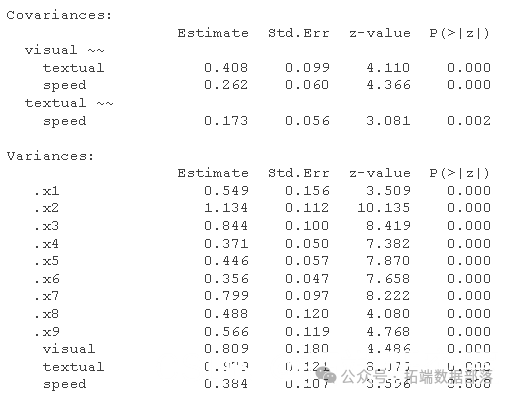
我们现在有一列“稳健”的全局拟合指数,并注意标准误差是使用 Huber-White 估计器估计的(对非正态性和聚类稳健)。
8 缺失数据
默认情况下, 通常会删除缺少任何变量的样本。但是您可能会丢失大量数据,并且因为它可能会给数据带来偏差。虽然远远超出了本教程,但通常最好在数据随机缺失的假设下使用所谓的全信息最大似然 (FIML),即给定变量的缺失可能与其他变量相关,但是而不是变量本身。使用 FIML,估计尝试根据具有可用数据的案例来估计所有参数。
以下是默认情况下发生的情况:
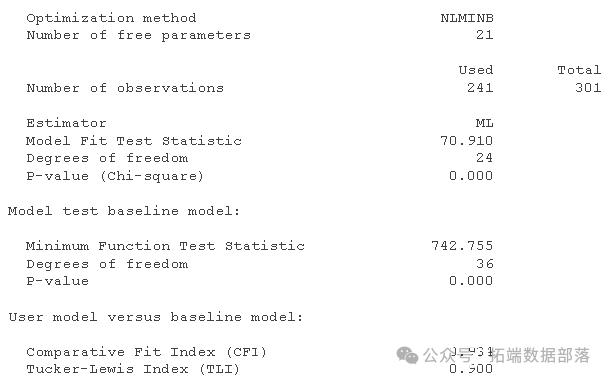

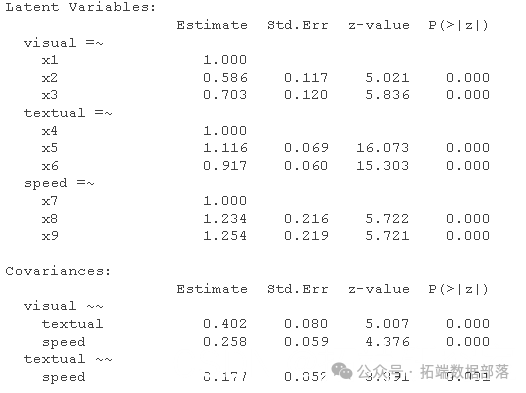
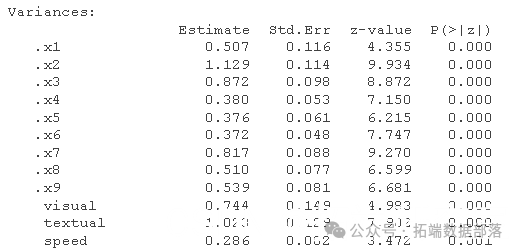
注意输出:

结果不理想。
好的,下面是FIML
summary(fiiml, fit.measures=TRUE)

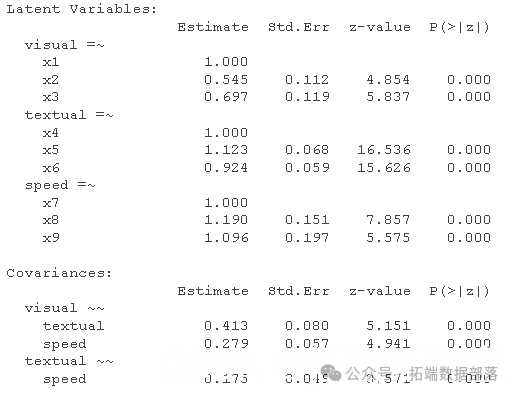
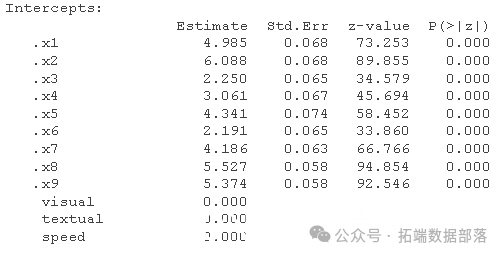
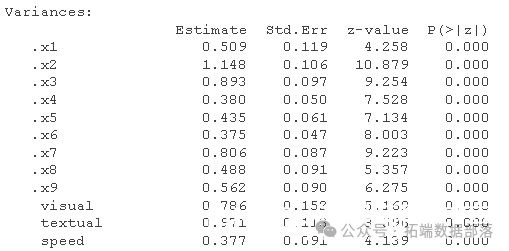
这更让人放心:

同样,关于缺失数据的理论和正式方法超出了本教程的范围,但我希望这能让大家了解到如何在sem中处理缺失问题。
关于分析师

Qiancheng Yu在杭州电子科技大学完成了统计学硕士学位。在此对他对本文的贡献表示诚挚感谢,他精通R语言,专注于机器学习和统计分析领域。擅长R语言编程、统计分析、机器学习建模等。
资料获取
在公众号后台回复“领资料”,可免费获取数据分析、机器学习、深度学习等学习资料。

点击文末“阅读原文”
获取全文完整代码数据资料。
本文选自《【视频讲解】偏最小二乘结构方程模型PLS-SEM分析白茶产业数字化对共同富裕的影响》。


点击标题查阅往期内容
R语言实现偏最小二乘回归法 partial least squares (PLS)回归
R语言中的block Gibbs吉布斯采样贝叶斯多元线性回归
R语言实现贝叶斯分位数回归、lasso和自适应lasso贝叶斯分位数回归分析
R语言用LOESS(局部加权回归)季节趋势分解(STL)进行时间序列异常检测
PYTHON用时变马尔可夫区制转换(MRS)自回归模型分析经济时间序列
R语言随机森林RandomForest、逻辑回归Logisitc预测心脏病数据和可视化分析
R语言生态学建模:增强回归树(BRT)预测短鳍鳗生存分布和影响因素
R语言实现偏最小二乘回归法 partial least squares (PLS)回归
Matlab中的偏最小二乘法(PLS)回归模型,离群点检测和变量选择
R语言如何找到患者数据中具有差异的指标?(PLS—DA分析)
结构方程模型SEM、路径分析房价和犯罪率数据、预测智力影响因素可视化2案例
结构方程模型 SEM 多元回归和模型诊断分析学生测试成绩数据与可视化
R语言结构方程SEM中的power analysis 效能检验分析
stata如何处理结构方程模型(SEM)中具有缺失值的协变量
R语言对用电负荷时间序列数据进行K-medoids聚类建模和GAM回归
R语言贝叶斯MCMC:用rstan建立线性回归模型分析汽车数据和可视化诊断
R语言深度学习:用keras神经网络回归模型预测时间序列数据
R语言贝叶斯MCMC:GLM逻辑回归、Rstan线性回归、Metropolis Hastings与Gibbs采样算法实例
R语言使用虚拟变量(Dummy Variables) 回归分析工资影响因素

![]()



