用通俗易懂的方式讲解：数据预处理归一化(附Python代码)_python数据归一化代码

技术答疑

本文来自技术群小伙伴的分享，想加入按照如下方式

目前开通了技术交流群，群友已超过3000人，添加时最好的备注方式为：来源+兴趣方向，方便找到志同道合的朋友

方式①、添加微信号：dkl88191，备注：来自CSDN+技术交流
方式②、微信搜索公众号：Python学习与数据挖掘，后台回复：加群+CSDN

一、为何要进行数据预处理？

• 任何收集而来的庞大数据往往是不可能一拿到就可以立马用得上的，比如一些数值大的数据，计算量复杂度高，不容易收敛，很难进行统计处理。

• 数据不符合正态分布，无法做一些符合正态分布的数学分析。

所以为了对数据进行更好的利用，我们需要使数据标准化。

二、数据标准化

数据无量纲化处理主要解决数据的可比性。数据标准化的方法有很多种，常用的有“最小—最大标准化”、“Z-score标准化”和“按小数定标标准化”等。

经过上述标准化处理，原始数据均转换为无量纲化指标测评值，即各指标值都处于同一个数量级别上，可以进行综合测评分析。这里我们重点讨论最常用的数据归一化处理，即将数据统一映射到[0,1]区间上。

1.归一化的目标

1.把数据转换为（0,1）区间的小数， 主要是为了数据处理方便提出来的，把数据映射到0～1范围之内处理，更加便捷快速。

2.把有量纲表达式变为无量纲表达式，解决数据的可比性。

2.归一化的优点

1.归一化后加快了梯度下降求最优解的速度，如果机器学习模型使用梯度下降法求最优解时，归一化往往非常有必要，否则很难收敛甚至不能收敛。

2.归一化有可能提高精度，一些分类器需要计算样本之间的距离（如欧氏距离），例如KNN。如果一个特征值域范围非常大，那么距离计算就主要取决于这个特征，从而与实际情况相悖（比如这时实际情况是值域范围小的特征更重要）。

3.哪些算法并不需要归一化

概率模型（树形模型）不需要归一化，因为它们不关心变量的值，而是关心变量的分布和变量之间的条件概率，如决策树、RF。而像Adaboost、SVM、LR、Knn、KMeans之类的最优化问题就需要归一化。

三、数据归一化方法

1.min-max标准化

通过遍历feature vector里的每一个数据，将Max和Min的记录下来，并通过Max-Min作为基数（即Min=0，Max=1）进行数据的归一化处理：其中Max为样本数据的最大值，Min为样本数据的最小值。

def MaxMinNormalization(x,Max,Min):
 
    x = (x - Min) / (Max - Min);
 
    return x;
1
2
3
4
5

使用numpy中的np.max()和np.min()就可找到最大和最小值。这种归一化方法比较适用在数值比较集中的情况。这种方法有个缺陷，如果max和min不稳定，很容易使得归一化结果不稳定，使得后续使用效果也不稳定。实际使用中可以用经验常量值来替代max和min。

ps: 将数据归一化到[a,b]区间范围的方法：

（1）首先找到原本样本数据X的最小值Min及最大值Max
（2）计算系数：k=（b-a)/(Max-Min)
（3）得到归一化到[a,b]区间的数据：Y=a+k(X-Min) 或者 Y=b+k(X-Max)

2.Z-score标准化

最常见的标准化方法就是Z标准化，也是SPSS中最为常用的标准化方法，spss默认的标准化方法就是z-score标准化。

也叫标准差标准化，这种方法给予原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。

def  Z_ScoreNormalization(x,mu,sigma):
 
    x = (x - mu) / sigma;
 
    return x;
1
2
3
4
5

numpy中mean和std函数，sklearn提供的StandardScaler方法都可以求得均值和标准差。标准化后的变量值围绕0上下波动，大于0说明高于平均水平，小于0说明低于平均水平。

下面使用numpy来实现一个矩阵的标准差标准化

import numpy as np

x_np = np.array([[1.5, -1., 2.],
[2., 0., 0.]])
mean = np.mean(x_np, axis=0)
std = np.std(x_np, axis=0)
print(‘矩阵初值为：{}’.format(x_np))
print(‘该矩阵的均值为：{}\n 该矩阵的标准差为：{}’.format(mean,std))
another_trans_data = x_np - mean
another_trans_data = another_trans_data / std
print(‘标准差标准化的矩阵为：{}’.format(another_trans_data))

矩阵初值为：[[ 1.5 -1. 2. ]
[ 2. 0. 0. ]]
该矩阵的均值为： [ 1.75 -0.5 1. ]
该矩阵的标准差为：[0.25 0.5 1. ]
标准差标准化的矩阵为：[[-1. -1. 1.]
[ 1. 1. -1.]]

下面使用sklearn提供的StandardScaler方法

from sklearn.preprocessing import StandardScaler # 标准化工具
import numpy as np

x_np = np.array([[1.5, -1., 2.],
[2., 0., 0.]])
scaler = StandardScaler()
x_train = scaler.fit_transform(x_np)
print(‘矩阵初值为：{}’.format(x_np))
print(‘该矩阵的均值为：{}\n 该矩阵的标准差为：{}’.format(scaler.mean_,np.sqrt(scaler.var_)))
print(‘标准差标准化的矩阵为：{}’.format(x_train))

矩阵初值为：[[ 1.5 -1. 2. ]
[ 2. 0. 0. ]]
该矩阵的均值为： [ 1.75 -0.5 1. ]
该矩阵的标准差为：[0.25 0.5 1. ]
标准差标准化的矩阵为：[[-1. -1. 1.]
[ 1. 1. -1.]]

以发现，sklearn的标准化工具实例化后会有两个属性，一个是mean_（均值），一个var_（方差）。最后的结果和使用numpy是一样的。

为什么z-score 标准化后的数据标准差为1？

x-μ只改变均值，标准差不变，所以均值变为0；(x-μ)/σ只会使标准差除以σ倍，所以标准差变为1。

3.Sigmoid函数：

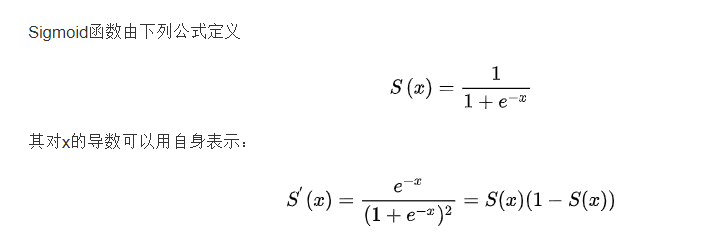
Sigmoid函数是一个具有S形曲线的函数，是良好的阈值函数，在(0, 0.5)处中心对称，在(0, 0.5)附近有比较大的斜率，而当数据趋向于正无穷和负无穷的时候，映射出来的值就会无限趋向于1和0。根据公式的改变，就可以改变分割阈值，这里作为归一化方法，我们只考虑(0, 0.5)作为分割阈值的点的情况：

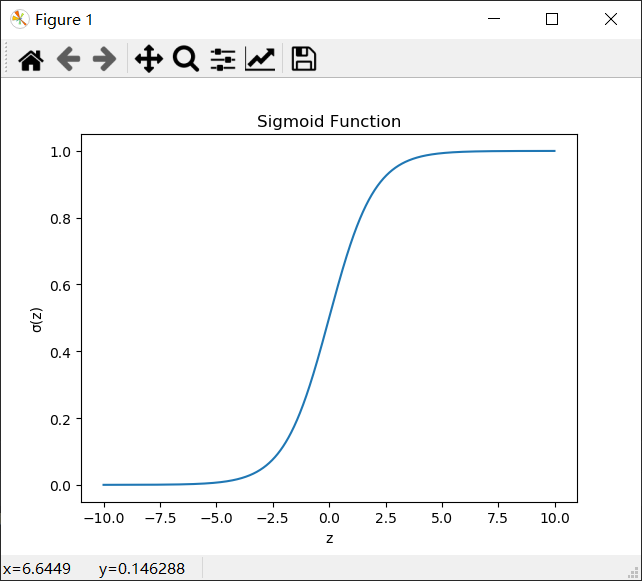
from matplotlib import pyplot as plt
import numpy as np
import math


def sigmoid_function(z):
    fz = []
    for num in z:
        fz.append(1 / (1 + math.exp(-num)))
    return fz


if __name__ == '__main__':
    z = np.arange(-10, 10, 0.01)
    fz = sigmoid_function(z)
    plt.title('Sigmoid Function')
    plt.xlabel('z')
    plt.ylabel('σ(z)')
    plt.plot(z, fz)
    plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

总结

主要还是对机器学习中的sklearn提供的StandardScaler方法后发现数据标准化这一概念，对大佬Friedman检验进一步理解。