pytorch搭建网络实现线性回归_pytorch搭建bp网络回归任务实例

pytorch搭建网络实现线性回归

生成数据集

为了简单起见，我们将根据带有噪声的线性模型构造一个人造数据集。 我们的任务是使用这个有限样本的数据集来恢复这个模型的参数。我们将使用低维数据，这样可以很容易地将其可视化。 在下面的代码中，我们生成一个包含1000个样本的数据集， 每个样本包含从标准正态分布中采样的2个特征。
我们使用线性模型参数$w=[2,-3.4{]}^T$、 $b=4.2$和噪声项$ϵ$生成数据集及其标签：
$$y=Xw+b+ϵ$$

def synthetic_data(w, b, num_examples):  
    """生成y=Xw+b+噪声"""
    X = torch.normal(0, 1, (num_examples, len(w)))
    y = torch.matmul(X, w) + b
    y += torch.normal(0, 0.01, y.shape)
    return X, y.reshape((-1, 1))

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)
1
2
3
4
5
6
7
8
9
10

通过生成第二个特征features[:, 1]和labels的散点图， 可以直观观察到两者之间的线性关系。

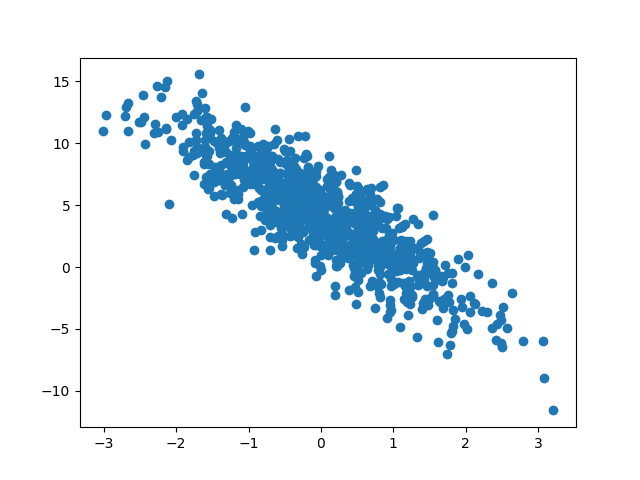
读取数据集

我们可以调用框架中现有的API来读取数据。 我们将features和labels作为API的参数传递，并通过数据迭代器指定batch_size。 此外，布尔值is_train表示是否希望数据迭代器对象在每个迭代周期内打乱数据。

def load_array(data_arrays, batch_size, is_train=True):  #@save
    """构造一个PyTorch数据迭代器"""
    dataset = torch.utils.data.TensorDataset(*data_arrays)
    return torch.utils.data.DataLoader(dataset, batch_size, shuffle=is_train)

batch_size = 10
data_iter = load_array((features, labels), batch_size)
1
2
3
4
5
6
7

为了验证是否正常工作，让我们读取并打印第一个小批量样本。 这里我们使用iter构造Python迭代器，并使用next从迭代器中获取第一项。

next(iter(data_iter))
1

[tensor([[ 0.7882, -0.7068],
         [ 0.5081,  0.2577],
         [-0.5769,  0.1545],
         [-0.3271, -0.6080],
         [-0.2716, -1.4628],
         [-1.1530, -1.4643],
         [ 0.1635, -0.2018],
         [-0.0753, -1.1161],
         [ 3.4251,  0.1953],
         [ 0.3589, -0.9478]]),
 tensor([[ 8.1742],
         [ 4.3357],
         [ 2.5157],
         [ 5.6106],
         [ 8.6395],
         [ 6.8726],
         [ 5.2155],
         [ 7.8377],
         [10.3918],
         [ 8.1590]])]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

定义模型

对于标准深度学习模型，我们可以使用框架的预定义好的层。这使我们只需关注使用哪些层来构造模型，而不必关注层的实现细节。 我们首先定义一个模型变量net，它是一个Sequential类的实例。 Sequential类将多个层串联在一起。 当给定输入数据时，Sequential实例将数据传入到第一层， 然后将第一层的输出作为第二层的输入，以此类推。
在下面的例子中，我们的模型只包含一个层，因此实际上不需要Sequential。 但是由于以后几乎所有的模型都是多层的，因此在这里使用Sequential来熟悉“标准的流水线”。
在PyTorch中，全连接层在Linear类中定义。 值得注意的是，我们将两个参数传递到nn.Linear中。 第一个指定输入特征形状，即2，第二个指定输出特征形状，输出特征形状为单个标量，因此为1。

from torch import nn

net = nn.Sequential(nn.Linear(2, 1))
1
2
3

初始化模型参数

在使用net之前，我们需要初始化模型参数。 如在线性回归模型中的权重和偏置。 深度学习框架通常有预定义的方法来初始化参数。 在这里，我们指定每个权重参数应该从均值为0、标准差为0.01的正态分布中随机采样， 偏置参数将初始化为零。
正如我们在构造nn.Linear时指定输入和输出尺寸一样， 现在我们能直接访问参数以设定它们的初始值。 我们通过net[0]选择网络中的第一个图层， 然后使用weight.data和bias.data方法访问参数。 我们还可以使用替换方法normal_和fill_来重写参数值。

net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)
1
2

定义损失函数

计算均方误差使用的是MSELoss类，也称为平方$L_2$范数。 默认情况下，它返回所有样本损失的平均值。

loss = nn.MSELoss()
1

定义优化算法

小批量随机梯度下降算法是一种优化神经网络的标准工具， PyTorch在optim模块中实现了该算法的许多变种。 当我们实例化一个SGD实例时，我们要指定优化的参数 （可通过net.parameters()从我们的模型中获得）以及优化算法所需的超参数字典。 小批量随机梯度下降只需要设置lr值，这里设置为0.03。

trainer = torch.optim.SGD(net.parameters(), lr=0.03)
1

训练

在每个迭代周期里，我们将完整遍历一次数据集（train_data）， 不停地从中获取一个小批量的输入和相应的标签。 对于每一个小批量，我们会进行以下步骤:

• 通过调用net(X)生成预测并计算损失l（前向传播）。
• 通过进行反向传播来计算梯度。
• 通过调用优化器来更新模型参数。

num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        l = loss(net(X) ,y)
        trainer.zero_grad()
        l.backward()
        trainer.step()
    l = loss(net(features), labels)
    print(f'epoch {epoch + 1}, loss {l:f}')
1
2
3
4
5
6
7
8
9

epoch 1, loss 0.000170
epoch 2, loss 0.000094
epoch 3, loss 0.000094
1
2
3

下面我们比较生成数据集的真实参数和通过有限数据训练获得的模型参数。 要访问参数，我们首先从net访问所需的层，然后读取该层的权重和偏置。

w = net[0].weight.data
print('w的估计误差：', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差：', true_b - b)
1
2
3
4

w的估计误差： tensor([2.0218e-04, 2.2173e-05])
b的估计误差： tensor([-1.4305e-05])
1
2

完整代码

import torch
from torch import nn


def synthetic_data(w, b, num_examples):
    """生成y=Xw+b+噪声"""
    X = torch.normal(0, 1, (num_examples, len(w)))
    y = torch.matmul(X, w) + b
    y += torch.normal(0, 0.01, y.shape)
    return X, y.reshape((-1, 1))


true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)


def load_array(data_arrays, batch_size, is_train=True):  #@save
    """构造一个PyTorch数据迭代器"""
    dataset = torch.utils.data.TensorDataset(*data_arrays)
    return torch.utils.data.DataLoader(dataset, batch_size, shuffle=is_train)


batch_size = 10
data_iter = load_array((features, labels), batch_size)
# print(next(iter(data_iter)))

# 定义网络模型
net = nn.Sequential(nn.Linear(2, 1))
# 初始化网络参数
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)
# 定义损失函数
loss = nn.MSELoss()
# 定义优化算法
trainer = torch.optim.SGD(net.parameters(), lr=0.03)

num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        l = loss(net(X), y)
        trainer.zero_grad()
        l.backward()
        trainer.step()
    l = loss(net(features), labels)
    print(f'epoch {epoch + 1}, loss {l:f}')


w = net[0].weight.data
print('w的估计误差：', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差：', true_b - b)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52