webgl变换矩阵理论详解_uniform mat4 matrix

---

前言

在webgl中将图形进行平移、旋转、缩放等操作时可以在着色器中使用数学表达式来操作，但是这样并不是最好的方式，当进行的变换比较复杂，如“旋转后平移再缩放”这样的场景，每次都要先重新计算表达式，然后在着色器中去更改它，这样很不方便，因此，出现了另一种数学手段——变换矩阵，变换矩阵非常适合处理计算机图形。本文对变换矩阵的理论进行讲解。

---

矩阵运算

矩阵是按照行列排列的一系列数值得的集合，由 m × n 个数排成的m行n列的数表称为m行n列的矩阵，简称m × n 矩阵，如下图。当 m 和 n 相同则称这个方阵为 m 阶矩阵(方阵)。

矩阵加减

应该注意的是只有同型矩阵之间才可以进行加减，即为行数和列数都必须一样的两个矩阵才可以进行加减运算。矩阵加减运算的规则是将将两个矩阵对应位置上的元素相加减：

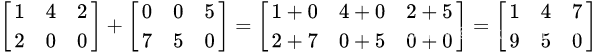
矩阵数乘

矩阵和标量相乘，返回一个新矩阵，新矩阵的各个元素等于原矩阵各个元素与标量的乘积：

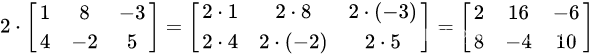
矩阵乘矩阵

两个矩阵的乘法仅当第一个矩阵A的列数和另一个矩阵B的行数相等时才能定义。如A是m×n矩阵和B是n×p矩阵，它们的乘积C是一个m×p矩阵，规则如下：

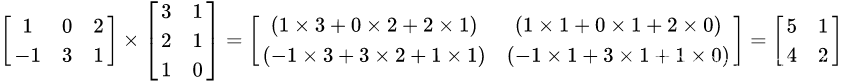
矩阵相乘满足分配律和结合律，但不满足交换律：

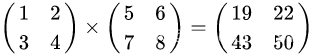
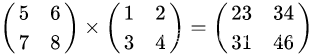
矩阵转置

把矩阵A的行和列互相交换所产生的矩阵称为A的转置矩阵$$A^T$$

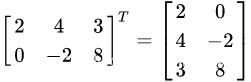
逆矩阵

设A是一个n阶矩阵，若存在另一个n阶矩阵B，使得： AB=BA=E ，则称方阵A可逆，并称方阵B是A的逆矩阵，单位矩阵是一个对角线上的元素都为1的方阵，其余元素为 0，比如下面就是一个 3 阶单位矩阵：

• 不是所有的矩阵都存在逆矩阵，逆矩阵首先必须是方阵，而且存在与其相乘结果为单位矩阵的矩阵
• 在图形学中，将进行矩阵变换的坐标再乘以该变换矩阵的逆矩阵，可以将变换后的坐标再还原回去，实现撤销的效果

正交矩阵

假设有一个方阵M，当且仅当 M 与其转置矩阵M^T的乘积等于单位矩阵时，称其为正交矩阵。即：

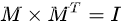
即：

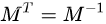
此时方阵M为一个正交矩阵，矩阵正交需要满足以下两个条件：

• 矩阵的每一行都是单位向量
• 矩阵的某一行和其他行向量相互垂直，点积为 0

两个向量a = [a1, a2,…, an]和b = [b1, b2,…, bn]的点积定义为：a·b=a1*b1 + a2*b2 + … + an*bn

矩阵变换的一般规则

行主序和列主序

在JavaScript中，没有专门用来表示矩阵的类型，需要使用类型化数组new Float32Array来存储，但是数组是一维的，矩阵是二维的，将二维的矩阵存储到一维数组中有两个方式：行主序和列主序。

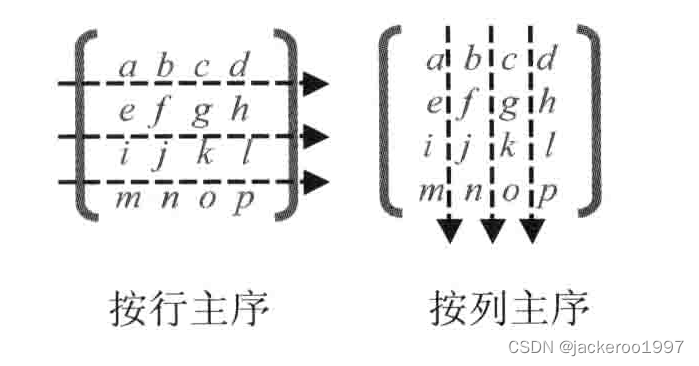
webgl按照列主序的规则将矩阵存储于数组，对于上面这个矩阵，按照列主序存到数组中一个是这样的：

 new Float32Array([ a,  e,  i,  m, b,  f,  j,  n,  c,  g,  k,  o, d,  h,  l,  p,]) 
1

一般在程序中这样书写，看起来更加舒服