动态规划基础概念_状态变量和决策变量

概念

动态规划是将一个问题划分为多个子步骤（或称之为阶段stage）。

其中有几个关键量：

1. 阶段k。动态规划第一步就是如何划分阶段。
2. 状态变量xk。描述系统当前阶段的状态。状态变量可以理解为用于决策的已知条件。
3. 决策变量uk。决策者在当前阶段做出的决策。 不同决策会组成一个完整的决策链，被称为策略。
4. 状态转移方程。从当前状态变量xk，做出决策以后，会得到下一状态变量x_k+1。 xk与x_k+1之间的关系就是状态转移方程。它就是个递推关系式。

例子

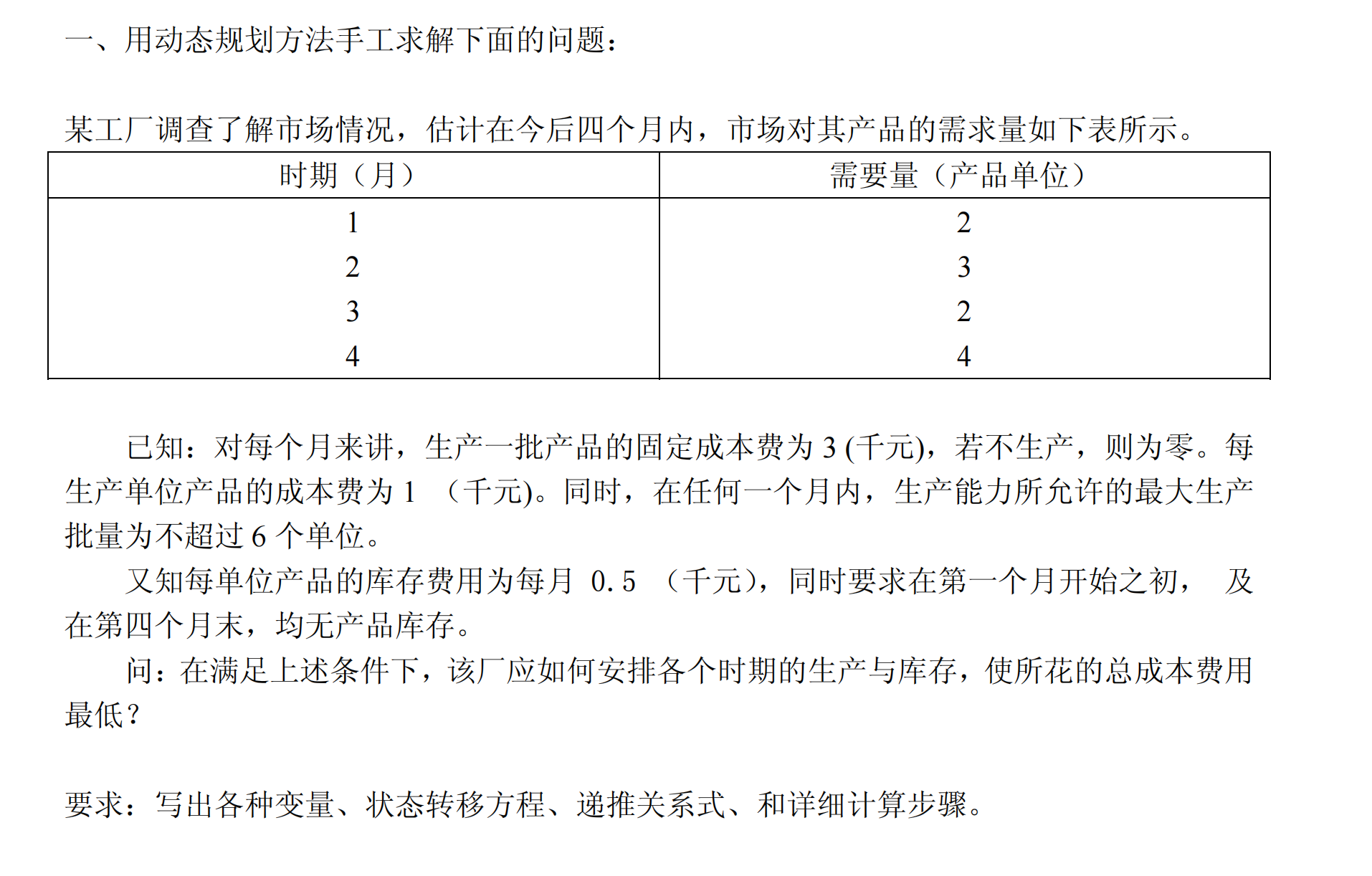
首先划分阶段：这个问题的阶段划分比较简单，显然每个月就是一个阶段。k表示第k月。

其次设定状态变量xk：设xk为第k个月初的库存量。状态变量是用来描述做决策的时候系统的状态的。这里最能描述系统当前状态的一个指标就是库存量。它会随着决策而变化。

然后设定决策量uk：问题是如何安排每个月的生产与库存。所以我们能够控制的就是生产量。因此决策变量uk为每个月的生产量。

最后是状态转移方程。即xk与x k+1之间的递推关系。

下个月的库存是这个月库存减去这个月需求，再加上这个月的生产量。我们设这个月需求为Nk，Nk是已知条件，如表中所示。

$$x_{k+1}=x_k-N_k+u_k$$

显然，状态变量xk和决策变量都受题目中的条件的制约。

1. 第1个月初和第4月末都要没有库存。
   即
   $$\begin{gathered} x_1=0 \\ {x}_5=0 \end{gathered}$$

2. 最大生产能力不超过6。显然也不会是负数。
   $$0\le u_k\le 6$$

3. 必须要让这个月满足需求。也就是说，这个月初库存加本月生产量，必须要大于需求量。
   $$x_k+u_k\ge N_k$$

我们想要把第三个式子解耦。因为它里面有两个未知量xk和uk。我们希望分别得到xk和uk的限制条件。于是结合条件1和条件2。

先确定xk的取值范围：
要保证x1=x5=0，必须同时考虑每月的需求量。
每个月初最少库存多少呢？0
每个月初最多库存多少呢？一个是每个月都按照最大生产能力来生产。当然要减去每月需求消耗。另外一个是未来总需求量，因为要保证最终库存为0。

$$0\le x_k\le min(6(k-1)-{\Sigma }_{i=1}^{k-1}{N}_i,{\Sigma }_{i=k}^4{N}_i)$$