算法归纳【数组篇】

二分查找

参考链接
https://programmercarl.com/0704.%E4%BA%8C%E5%88%86%E6%9F%A5%E6%89%BE.html#%E6%80%9D%E8%B7%AF

1. 前提条件：

1. 数组为有序数组，
2. 无重复元素：因为一旦有重复元素，使用二分查找法返回的元素下标可能不是唯一的。

2. 二分查找边界

1. [left, right]区间：while (left <= right) 要使用 <= ，因为left == right是有意义的，所以使用 <=
   if (nums[middle] > target) right 要赋值为 middle - 1，因为当前这个nums[middle]一定不是target，那么接下来要查找的左区间结束下标位置就是 middle - 1

func search(nums []int, target int) int {
    high := len(nums)-1
    low := 0
    for low <= high {
        mid := low + (high-low)/2
        if nums[mid] == target {
            return mid
        } else if nums[mid] > target {
            high = mid-1
        } else {
            low = mid+1
        }
    }
    return -1
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

2. 区间[left, right)：while (left < right)，这里使用 < ,因为left == right在是没有意义的
   if (nums[middle] > target) right 更新为 middle，因为当前nums[middle]不等于target，去左区间继续寻找，而寻找区间是左闭右开区间，所以right更新为middle，即：下一个查询区间不会去比较nums[middle]

func search(nums []int, target int) int {
    high := len(nums)
    low := 0
    for low < high {
        mid := low + (high-low)/2
        if nums[mid] == target {
            return mid
        } else if nums[mid] > target {
            high = mid
        } else {
            low = mid+1
        }
    }
    return -1
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

====================================================================

2.移除元素

参考链接
https://programmercarl.com/0027.%E7%A7%BB%E9%99%A4%E5%85%83%E7%B4%A0.html#%E7%AE%97%E6%B3%95%E5%85%AC%E5%BC%80%E8%AF%BE

数组的元素在内存地址中是连续的，不能单独删除数组中的某个元素，只能覆盖。 所以不可以删除，只能将等于val的值移到后面，最后的结果返回数组满足条件的前半部分即可

func removeElement(nums []int, val int) int {
    left, right := 0, len(nums)-1
    for left <= right {
        if nums[left] == val {
            nums[left] = nums[right]
            right--
        } else {
            left++
        }
    }
    return left
}


1
2
3
4
5
6
7
8
9
10
11
12
13
14

顺便从二分法学以致用：【关于 left <= right 和 left < right 的选择问题】

func removeElement(nums []int, val int) int {
    left, right := 0, len(nums)
    for left < right {
        if nums[left] == val {
            nums[left] = nums[right-1]
            right--
        } else {
            left++
        }
    }
    return left
}
1
2
3
4
5
6
7
8
9
10
11
12

=================================================================

有序数组的平方

参考链接
https://programmercarl.com/0977.%E6%9C%89%E5%BA%8F%E6%95%B0%E7%BB%84%E7%9A%84%E5%B9%B3%E6%96%B9.html#%E5%85%B6%E4%BB%96%E8%AF%AD%E8%A8%80%E7%89%88%E6%9C%AC

双指针法
数组其实是有序的， 只不过负数平方之后可能成为最大数了。
那么数组平方的最大值就在数组的两端，不是最左边就是最右边，不可能是中间。
此时可以考虑双指针法了，i指向起始位置，j指向终止位置。
定义一个新数组result，和A数组一样的大小，让k指向result数组终止位置。
如果A[i] * A[i] < A[j] * A[j] 那么result[k–] = A[j] * A[j]; 。
如果A[i] * A[i] >= A[j] * A[j] 那么result[k–] = A[i] * A[i]; 。

func sortedSquares(nums []int) []int {
	n := len(nums)
	i, j, k := 0, n-1, n-1
	ans := make([]int, n)
	for i <= j {
		lm, rm := nums[i]*nums[i], nums[j]*nums[j]
		if lm > rm {
			ans[k] = lm
			i++
		} else {
			ans[k] = rm
			j--
		}
		k--
	}
	return ans
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

========================================================

长度最小的子数组

参考链接
https://programmercarl.com/0209.%E9%95%BF%E5%BA%A6%E6%9C%80%E5%B0%8F%E7%9A%84%E5%AD%90%E6%95%B0%E7%BB%84.html#%E7%AE%97%E6%B3%95%E5%85%AC%E5%BC%80%E8%AF%BE

给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组，并返回其长度。如果不存在符合条件的子数组，返回 0。
示例：
输入：s = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

滑动窗口

func minSubArrayLen(target int, nums []int) int {
	if len(nums) == 0 {
		return 0
	}

	slow, fast := 0, 0
	sum := nums[0]
	minLen := len(nums) + 1
	for fast < len(nums) {
		if sum >= target {
			minLen = min(minLen, fast-slow+1)
			//还要记住改变sum的值，否则就会带着sum=7这个结果一直循环
			sum = sum - nums[slow]
			slow++
			
		} else if sum < target {
			fast++
			if fast < len(nums) {
				sum = sum + nums[fast]
			}
		} 
	}

	if minLen == len(nums)+1 {
		return 0
	}
	return minLen
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

=========================================================

59.螺旋矩阵II

给定一个正整数 n，生成一个包含 1 到 n^2 所有元素，且元素按顺时针顺序螺旋排列的正方形矩阵。
示例:
输入: 3
输出: [ [ 1, 2, 3 ], [ 8, 9, 4 ], [ 7, 6, 5 ] ]

参考链接
https://programmercarl.com/0059.%E8%9E%BA%E6%97%8B%E7%9F%A9%E9%98%B5II.html#%E7%AE%97%E6%B3%95%E5%85%AC%E5%BC%80%E8%AF%BE

每画一条边都要坚持一致的左闭右开，或者左开右闭的原则，这样这一圈才能按照统一的规则画下来

//左开右闭
func generateMatrix(n int) [][]int {
    top, bottom := 0, n-1
    left, right := 0, n-1
    num := 1
    tar := n * n
    matrix := make([][]int, n)
    for i := 0; i < n; i++ {
        matrix[i] = make([]int, n)
    }
    for num <= tar {
        for i := left; i <= right; i++ {
            matrix[top][i] = num
            num++
        }
        top++
        for i := top; i <= bottom; i++ {
            matrix[i][right] = num
            num++
        }
        right--
        for i := right; i >= left; i-- {
            matrix[bottom][i] = num
            num++
        }
        bottom--
        for i := bottom; i >= top; i-- {
            matrix[i][left] = num
            num++
        }
        left++
    }
    return matrix
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

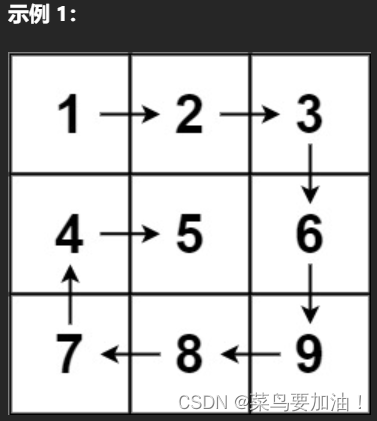
54. 螺旋矩阵

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

func spiralOrder(matrix [][]int) []int {
	result := []int{}

	//矩阵先考虑条件
	if len(matrix) == 0 || len(matrix[0]) == 0 {
		return result
	}

	m, n := len(matrix), len(matrix[0])
	left, right, top, bottom := 0, n-1, 0, m-1

	for left <= right && top <= bottom {
		// 从左到右
		for i := left; i <= right; i++ {
			result = append(result, matrix[top][i])
		}
		// 从上到下
		for i := top + 1; i <= bottom; i++ {
			result = append(result, matrix[i][right])
		}
		// 从右到左，确保有多行
		// 在螺旋顺时针遍历矩阵的过程中，从右到左的遍历应该在确保存在多行的情况下进行。如果只有一行，那么从右到左的遍历就没有意义，因为在上一步已经从左到右遍历过了。因此，通过 if top < bottom 进行判断，可以确保在有多行的情况下才进行从右到左的遍历。
        //  比如 6->7的过程，因为经过一轮之后top=1，bottom=1，此时6->7是从左到右，不需要从右到左，下面的left < right同理
		if top < bottom {
			for i := right - 1; i >= left; i-- {
				result = append(result, matrix[bottom][i])
			}
		}
		// 从下到上，确保有多列
		if left < right {
			for i := bottom - 1; i > top; i-- {
				result = append(result, matrix[i][left])
			}
		}
		left++
		right--
		top++
		bottom--
	}

	return result
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43