损失函数MSE和MAE的区别以及如何选择_mse损失

1、均方误差（L2损失）

均方误差(MSE)是最常用的回归损失函数，计算方法是求预测值与真实值之间距离的平方和，公式如下：

$MSE=\frac{1}{m}{\sum }_m^{i=1}{\left(y_i-{\hat{y}}_i\right)}^2$

下图是MSE函数的图像，其中目标值是100，预测值的范围从-10000到10000，Y轴代表的MSE取值范围是从0到正无穷，并且在预测值为100处达到最小。通过数值模拟，平均绝对值误差的形状如下：

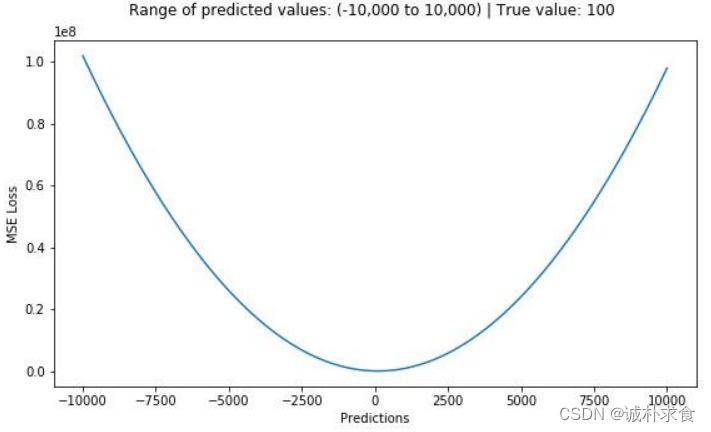
2、平均绝对值误差（L1损失）

$MAE=\frac{1}{m}{\sum }_m^{i=1}\left|\left(y_i-{\hat{y}}_i\right)\right|$

平均绝对误差（MAE）是另一种用于回归模型的损失函数。MAE是目标值和预测值之差的绝对值之和。其只衡量了预测值误差的平均模长，而不考虑方向，取值范围也是从0到正无穷（如果考虑方向，则是残差/误差的总和——平均偏差（MBE））。

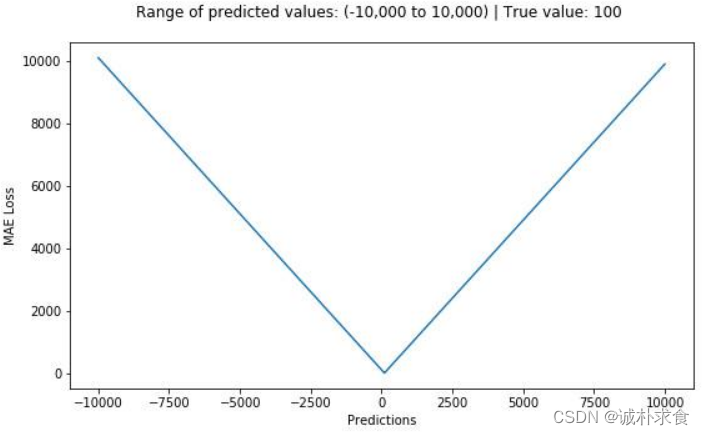
3、MSE（L2损失）与MAE（L1损失）的比较

简单来说，MSE计算简便，但MAE对异常点有更好的鲁棒性。下面就来介绍导致二者差异的原因。

训练一个机器学习模型时，我们的目标就是找到损失函数达到极小值的点。 当预测值等于真实值时，这两种函数都能达到最小。

下面是这两种损失函数的python代码。你可以自己编写函数，也可以使用sklearn内置的函数。

# true: Array of true target variable
# pred: Array of predictions
def mse(true, pred):
    return np.sum((true - pred)**2)/len(true)
def mae(true, pred):
    return np.sum(np.abs(true - pred))/len(true)
# also available in sklearn
# from sklearn.metrics import mean_squared_errorfrom 
# sklearn.metrics import mean_absolute_error
1
2
3
4
5
6
7
8
9

下面让我们观察MAE和RMSE（即MSE的平方根，同MAE在同一量级中）在两个例子中的计算结果。第一个例子中，预测值和真实值很接近，而且误差的方差也较小。第二个例子中，因为存在一个异常点，而导致误差非常大。

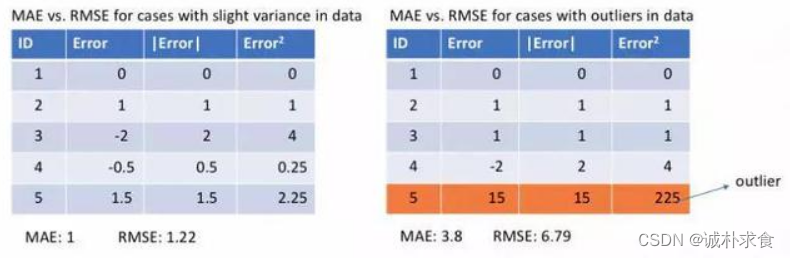
4、MSE与MAE各自的优缺点

1、MSE对误差取了平方（令e=真实值-预测值），因此若e>1，则MSE会进一步增大误差。如果数据中存在异常点，那么e值就会很大，而e则会远大于|e|。因此，相对于使用MAE计算损失，使用MSE的模型会赋予异常点更大的权重。在第二个例子中，用RMSE计算损失的模型会以牺牲了其他样本的误差为代价，朝着减小异常点误差的方向更新。然而这就会降低模型的整体性能。如果训练数据被异常点所污染，那么MAE损失就更好用（比如，在训练数据中存在大量错误的反例和正例标记，但是在测试集中没有这个问题）。

2、直观上可以这样理解：如果我们最小化MSE来对所有的样本点只给出一个预测值，那么这个值一定是所有目标值的平均值。但如果是最小化MAE，那么这个值，则会是所有样本点目标值的中位数。众所周知，对异常值而言，中位数比均值更加鲁棒，因此MAE对于异常值也比MSE更稳定。

3、MAE存在一个严重的问题（特别是对于神经网络）：更新的梯度始终相同，也就是说，即使对于很小的损失值，梯度也很大。这样不利于模型的学习。为了解决这个缺陷，我们可以使用变化的学习率，在损失接近最小值时降低学习率。而MSE在这种情况下的表现就很好，即便使用固定的学习率也可以有效收敛。MSE损失的梯度随损失增大而增大，而损失趋于0时则会减小。这使得在训练结束时，使用MSE模型的结果会更精确。

5、MSE与MAE如何选择

如果异常点代表在商业中很重要的异常情况，并且需要被检测出来，则应选用MSE损失函数。相反，如果只把异常值当作受损数据，则应选用MAE损失函数。总的来说，处理异常点时，MAE损失函数更稳定，但它的导数不连续，因此求解效率较低。MSE损失函数对异常点更敏感，但通过令其导数为0，可以得到更稳定的封闭解。

当两者问题同时存在时，就需要考虑其他的更合适的损失函数了，如Huber损失(平滑的平均绝对误差)、Log-Cosh损失、分位数损失等，详见：

机器学习大牛最常用的5个回归损失函数，你知道几个？