异构群体机器人协作任务分配（群体智能论文学习）_群体智能领域论文

异构群体机器人协作任务分配（群体智能论文学习）

1、题外话：无人机集群发展个人浅见

当前限制无人机集群发展的技术瓶颈有：1、通信。带宽窄、自组网络难以达成、对wifi、4g或者zigbee的基站要求高，无法实现完全脱离中心通信的问题，这也是实现无人集群自主zz的关键问题。2、能源。目前小型无人机的运行时间基本在1h以下，多为半个小时，这与无人的耗能大、能源技术有限都有关，这也限制了无人机可携带负载、可覆盖区域、可处理计算等能力。3、自主性和智能性。当前的无人机智能还处于初级阶段，主要解决自主避碰和编队等基本问题，还未涉及更高级的飞行动作，态势分析能力弱，计算能力低下导致复杂算法并不能在机载计算机上实现，种种约束导致了当前无人机自主智能。

当前5G技术的发展将会助力物联网时代的到来，也是无人时代的到来，极大可能解决不依托固定基站的无人机自组织网络的构建问题。能源技术也在不断发展，新能源汽车的快速发展也代表未来将会有更多的电力充电站、电池技术也将更加成熟，如果同样大小的电池能够提供更多电能，将极大解放无人集群的能力边界。人工智能是当代最热门的IT领域，图像识别能力、数据分析能力都在不断提升，里程碑式出现了alphaGo，alphaZero等打败人类最高围棋水平的人工智能，同时在机器人、飞行器制作等方面的技术也在不断提升，实现特技飞行、携带机枪等武器的无人机也已有了原型机。这些技术的发展趋势将会很好的解决当前制约无人机的几个难点。

2、无人机集群在科幻电影中的精彩应用

感兴趣的可以看看在电影《蜘蛛侠2》中的无人机应用模式。（链接传送）

3、进入正题：群体机器人协同任务分配问题

群体机器人系统由于其冗余性、同时执行不同任务的能力以及容错能力，越来越多地被用于实现动态和复杂的目标[1,2]。然而，对于大型机器人群体，群体协调问题变得非常复杂，通常需要机器人之间的通信或能够访问群体全局信息的中心协调器[3]。这推动了分散协调控制算法的发展，其中机器人之间的简单交互导致实现各种目标所需的涌现特性，例如几何形态[4]，任务分配[5,6]，或者覆盖一个区域[7]。

在群体机器人的众多任务中，分布式任务分配问题在近年来的控制和机器人学文献中得到了广泛的关注。最基本的问题是，一组机器人应该选择一个特定的任务，以便在多个候选任务之间进行最优分配。解决这些问题的许多工作已经被研究为基于博弈论的协商算法[8，9]、动态目标分配问题[10-15]、网络上的量化共识[16-18]或任务分配的随机策略[19，20]。这些动态分配方法通常需要机器人之间的显式通信。

与前面的研究工作不同，基于群体智能的任务分配算法的灵感来源于群居昆虫由于其在群体中的自我组织和自我调节能力而成为集体行为。一个有趣的特征是在昆虫群落中经常发现的分工：蚂蚁的觅食和筑巢防御[21]，蜜蜂的觅食和护理[22]，花蜜和花粉收集[23]都是分工的例子。个体昆虫对环境的感知和认识非常有限，没有集中的协调机制来指导社会昆虫的合作行为。尽管它们的能力有限，但它们通过相互作用提高了整个系统的有效性、效率和鲁棒性，并展示了自适应任务分配以获得群体生存的共同目标。

对于分布式执行任务的机器人集群来说，这类生物启发式任务分配方法由于不依赖机器人间通信，可以很好适应拒止环境，且可以很容易地部署在性能有限的大规模廉价机器人上，不需要机器人之间的广泛协调，并且对意外的机器人故障具有鲁棒性，因此非常有吸引力。

许多基于群体智能的任务分配方法已经被提出[24-28]。在众多模型中，我们主要关注响应阈值模型[26, 27]。该模型基于对昆虫群体集体行为的观察，特别是蜜蜂和蚂蚁所做的工作，并提出了一个使用响应阈值调节分工的简单数学模型[29,27]。单个智能体基于任务强度和确定个体对执行任务的响应趋势的相应响应阈值来响应执行任务。根据不同的响应阈值，对同一任务强度产生不同的响应，这一特性决定了单个智能体是否有执行任务的倾向。这些特点对许多应用领域的研究都是一种启发，基于这个模型已经完成了许多不同的工作[30-34]。

基于响应阈值的任务分配由于其分工是通过简单的规则来实现的，因此得到了广泛的研究。在这个模型中，获得合适的阈值分布对于获得期望的劳动分工很重要，并且研究了使用固定阈值或可变阈值的各种工作。首先，研究了固定响应阈值模型作为解释分工规律的重要理论[27]。在群居昆虫中，两种普遍的模式在分工中起着一定的作用：年龄相关的任务执行模式和不同的工人的大小和/或形状[35]。已经研究了动态适应阈值的改进版本[36]，其中研究了wasp群体如何协调100个个体活动和分配任务的计算模型。该模型基于强化学习模型[37]调节阈值以获得最佳阈值。执行后，通过降低执行任务的阈值和增加未执行其他任务的阈值来更新阈值。在这些重复行为的基础上，每一个个体对特定的任务都有一种专业化的倾向，这种倾向在一个群体中产生了更有效的分工。使用人工神经网络优化响应阈值模型[38]。

在蜂群中，人们知道工蜂的年龄与它们通常执行的任务之间存在着相关性[39-44]。较年轻的工人执行内部任务（育儿护理和鸟巢维护），较年长的工人在蜂巢外执行觅食和防御任务。然而，这种趋势可以通过群体成员的年龄分布来灵活地改变。例如，在幼龄蜜蜂比例较高的群体中，蜜蜂开始觅食任务的年龄低于正常群体，年长蜜蜂的存在会延迟或抑制群体中其他幼龄蜜蜂生理年龄的发育。在Huang和Robinson的工作（1996）中，研究表明蜜蜂之间的工蜂相互作用驱动荷尔蒙调节机制，导致社会抑制。这一事实被用于基于社会抑制的任务分配的其他研究中[42-44]。Jones和Mataric（2006）对类似问题进行了研究，提出了一种基于数学模型的分工机制。其他有趣的研究集中在处理机器人群中任务分配的任务转移率[45, 46, 19]，并表明适当选择任务转移率可以指导所需的任务分配。此外，还研究了描述任务转移动力学的宏观分析模型[20]。

4、典型文章分析（7篇）

（1）群体机器人系统任务分配的自适应调节方法

在群体机器人系统中，任务分配问题一直是一个具有挑战性的问题。本文研究了多机器人在给定时间范围内并行采集多个目标的动态任务分配问题。提出了一种无需机器人间通信的响应阈值模型分散策略。在这里，我们为每个机器人引入了一个任务选择概率函数，以平衡任务需求和执行任务的机器人。该方法通过改变任务选择概率函数中给定的响应阈值，可以产生任务的变化趋势。使用此属性，每个机器人可以通过调整响应阈值在所有可用任务中选择自己的任务。这最终会在组级别促进所需的任务分布，并减少任务更改的数量。我们的方法建议根据最近观察到的物体和邻近机器人在周围区域观察到的任务来更新机器人的响应阈值。我们提供了一个收敛性分析，即系统可以随机收敛到期望任务分布的平衡点。即使只有局部的环境信息被赋予个体机器人，这种方法也是有效的。通过对多机器人执行觅食任务的仿真，验证了该方法的有效性，并给出了一个动态的任务分配过程[47]。

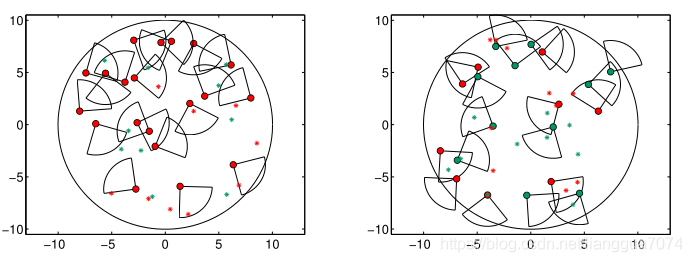
评述：该文章探讨了两类机器人（红绿，完成对应颜色的觅食任务），实验分析比较完善，但运动模型、任务模型、通信模型建立偏简单，有较大改进空间。

（2）面向时间约束任务的局部蚁群算法

我们提出了一种新的蚁群优化算法应用于有效地将一组齐次机器人分配给一组需要在特定期限内完成的任务。我们利用机器人之间的局部通信来周期性地评估分配方案的质量，并且智能体在高质量的方案中独立选择。使用信息素跟踪进行评估，以支持最小化任务执行时间的分配。我们的方法在静态和动态环境（即任务可用性随时间而变化）中使用不同的基于物理的模拟集进行了验证[48]。

评述：缺乏对照实验，只是针对自己工作不同的参数配置来进行实验分析；缺乏实机实验。

（3）基于机器人相遇的机器人群闭环任务分配

在群体机器人系统中，协调行为是通过机器人之间以及机器人与环境之间的局部交互而产生的。对于在封闭区域内执行一组预先定义的任务的机器人群，本文提出了一种分散机制，利用机器人在区域内移动时发生的空间交互，将任务分配给每个机器人。为了获得执行每项任务所需的群体百分比，开发的策略允许个体机器人在区域内遇到其他机器人时，以一定的概率在不同任务之间切换。我们利用Enskog稠密气体理论的思想，建立了一个分析模型来描述在稠密的机器人群中发生的机器人间相遇，并说明了群体如何利用这个模型来达到所需的分配水平。此外，机器人之间的相遇使机器人能够测量当前的温度分配，而温度的分配是使用或调节的在任务之间切换。这个根据当前分配与所需值之间的距离，允许软件接受或降低任务之间的传输速率，最终促进不间断任务由机器人执行。本文介绍的方法说明了如何利用群体中机器人之间自然发生的相遇，以闭环的方式将任务分配给机器人。所开发的算法是完全分散的，可以部署到最小的机器人上，以满足通信的需要。在一组实际机器人上验证了该算法的性能[49]。

（4）基于响应阈值Sigmoid模型的觅食机器人群体自主任务分配

本文提出了一个任务分配模型，用于在一群觅食机器人中自动调整工作机器人的数量。在群体觅食中，觅食区的交通拥挤和机器人之间的物理干扰会显著降低群体的性能。首次引入交通流密度的概念，用以反映觅食区的交通状况。避障量是指群体觅食过程中产生的物理干扰次数。交通流密度和避障量共同调整阈值。在提出的响应阈值sigmoid模型（RTSM）中，个体机器人可以根据阈值和外部刺激自主决定是否觅食，群体系统可以完成预期的觅食任务。为了评价该方法的性能，进行了仿真实验。介绍了几种性能指标对实验结果进行分析，并与自适应响应阈值模型（ARTM）进行了比较。实验结果表明，RTSM提高了觅食效率，减少了物理干扰[50]。

（5）复杂任务中机器人群的人工进化自主任务分配

群体机器人学是一个多机器人在没有任何形式的集中控制的情况下，自主地协调集体行为以完成给定任务的领域。在群体机器人中，任务分配是指机器人在不同的子任务上动态分布的行为，这是解决复杂任务所必需的。进化机器人技术是发展机器人群体集体行为的一种很有前途的方法。然而，人工进化常常会遇到两个问题：自举问题和欺骗问题，特别是当底层任务非常复杂时。为了克服这些困难，本文提出了一种由任务划分和自主任务分配两步组成的方案。我们进行了计算机模拟实验，其中机器人群必须完成一个复杂的集体觅食问题，结果表明，所提出的方法比传统的进化机器人方法更有效[51]。

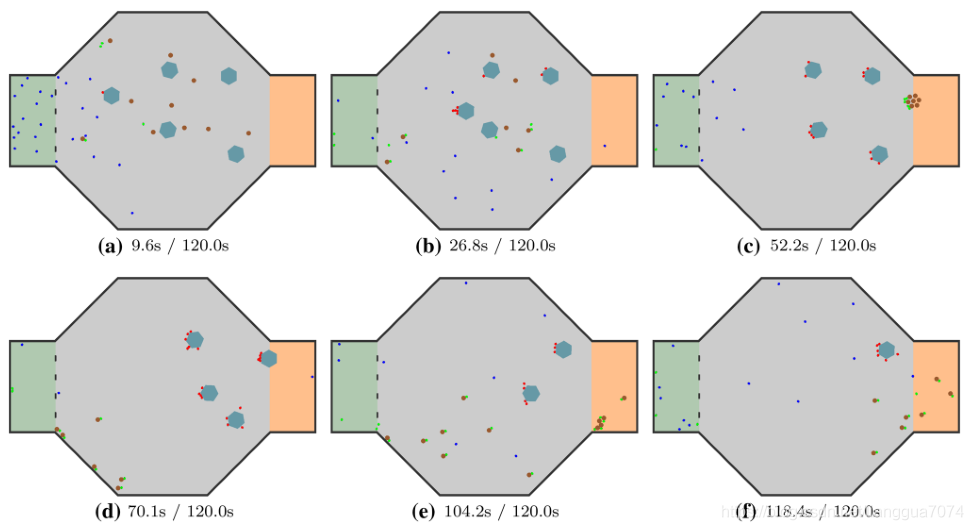
（6）基于局部交互的可扩展群体机器人系统中的自主角色分配与任务分配

提出了一种基于响应阈值模型的可扩展群体机器人系统局部交互自主角色分配和任务分配方法。响应阈值描述了蚂蚁对信息素的敏感性。在现实生活中，存在着信息素敏感性高和低的蚂蚁。蚂蚁的信息素敏感性与自主角色分配和任务分配有关。在传统的响应阈值模型中，假设一只蚂蚁可以获得蚁群中所有工人的数量。然而，蚂蚁的功能非常有限，很难获得和处理所有的工作人员。因此，我们使用一个响应阈值模型，该模型引用所遇到的觅食蚂蚁的数量，而不是所有工作人员的数量。在本研究中，我们将所提出的方法应用于蚁群觅食问题，并展示了所提出方法在动态环境下的稳健性[52]。

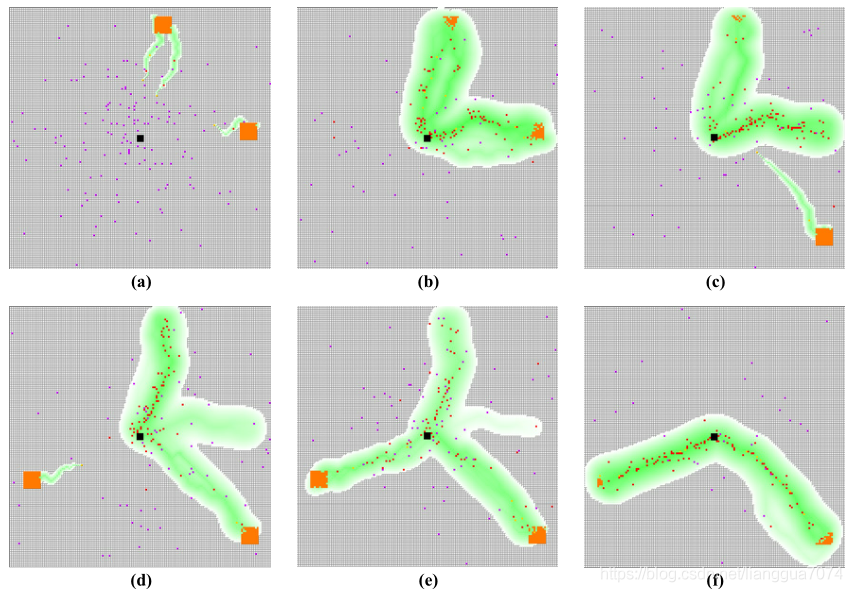
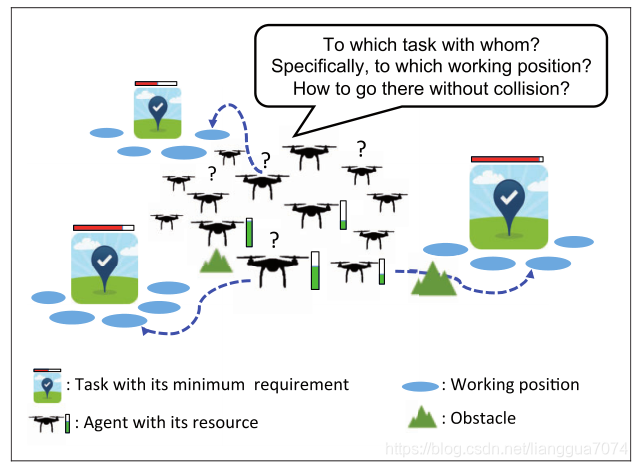
（7）异构空中机器人群最小需求协同任务的集成决策框架

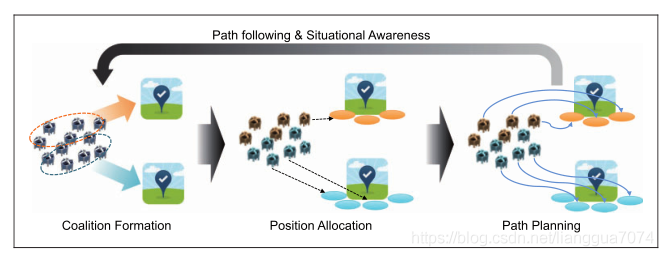
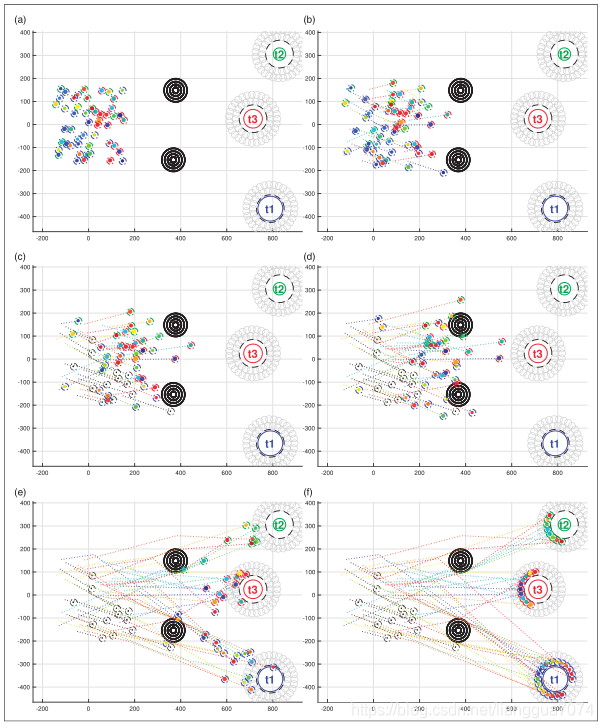
在多任务空间分布的协同任务环境下，空中机器人群的决策问题包括团队组建、团队对任务分配、agent对工作位置分配和避免碰撞的轨迹优化。当涉及到异构智能体、任务的最小需求和公平分配时，问题变得更加复杂。本文将所有的组合问题列为一个优化问题，然后提出一个以分散方式解决问题的集成框架。我们将复杂的原始问题近似分解为三个子问题（即联盟形成、位置分配和路径规划），这些子问题由三个不同的模块依次处理。以博弈论为基础的联盟形成模块处理一个最大-最小问题，其目标是将代理划分成不相交的任务特定团队，使代理的工作资源与任务的最小工作量要求成比例。对于分配给同一任务的代理，在合理的假设下，位置分配子问题可以从计算复杂度的角度得到有效的解决。在轨迹优化方面，我们采用了模型预测控制和序列凸规划算法，减小了问题的规模，使智能体能够实时生成无碰撞的轨迹。作为概念验证，将该框架应用于无人机群协同待命干扰任务场景中，通过数值实验验证了其可行性、容错性和近似最优性[53]。

参考文献

[1] Brambilla, M., Ferrante, E., Birattari, M., & Dorigo, M. (2013). Swarm robotics: A review from the swarm engineering perspective. Swarm Intelligence, 7(1), 1–41.
[2] Sahin, E. (2005). Swarm robotics: From sources of inspiration to domains of application. In E. ¸ Sahin & W. M. Spears (Eds.), Swarm robotics (pp. 10–20). Berlin: Springer.
[3] Iocchi, L., Nardi, D., & Salerno, M. (2001). Reactivity and deliberation: A survey on multi-robot systems. In M. Hannebauer & J. Wendler (Eds.), Balancing reactivity and social deliberation in multi-agent systems (pp. 9–32). Berlin: Springer.
[4] Cheah, C. C., Hou, S. P ., & Slotine, J. J. E. (2009). Region-based shape control for a swarm of robots. Automatica, 45(10), 2406–2411.
[5] Berman, S., Halász, Á., & Hsieh, M. (2016). Ant-inspired allocation: Top-down controller design for distributing a robot swarm among multiple tasks (pp. 243–274). Boca Raton: CRC Press.
[6] Berman, S., Halász, Á., Hsieh, M. A., & Kumar, V . (2009). Optimized stochastic policies for task allocation in swarms of robots. IEEE Transactions on Robotics, 25(4), 927–937.https://doi.org/10.1109/TRO.2009.2024997.
[7] Cortes, J., Martinez, S., Karatas, T., & Bullo, F. (2004). Coverage control for mobile sensing networks. IEEE Transactions on Robotics and Automation, 20(2), 243–255.
[8] G. Arslan, J. R. Marden, J. S. Shamma, Autonomous vehicle-target assignment:
A game-theoretical formulation, Journal of Dynamic Systems, Measurement, and
Control 129 (5) (2007) 584–596.
[9] R. Cui, J. Guo, B. Gao, Game theory-based negotiation for multiple robots task 560
allocation, Robotica 31 (06) (2013) 923–934.
[10] D. Castanon, C. Wu, Distributed algorithms for dynamic reassignment, in: Decision
and Control, 2003. Proceedings. 42nd IEEE Conference on, Vol. 1, IEEE, 2003, pp.
13–18.
[11] S. L. Smith, F. Bullo, Monotonic target assignment for robotic networks, Automatic 565
Control, IEEE Transactions on 54 (9) (2009) 2042–2057.
[12] D. Zou, H. Liu, L. Gao, S. Li, An improved differential evolution algorithm for the
task assignment problem, Engineering Applications of Artificial Intelligence 24 (4)
(2011) 616–624.
[13] A. T. Tolmidis, L. Petrou, Multi-objective optimization for dynamic task allocation 570
in a multi-robot system, Engineering Applications of Artificial Intelligence 26 (5)
(2013) 1458–1468.
[14] W. Lee, D. Kim, Handling interference effects on foraging with bucket brigades,
Bioinspiration & biomimetics 12 (6) (2017) 066001.
[15] W. Lee, D. Kim, Autonomous shepherding behaviors of multiple target steering 575
robots, Sensors 17 (12) (2017) 2729.
[16] A. Kashyap, T. Ba¸ sar, R. Srikant, Quantized consensus, Automatica 43 (7) (2007)
1192–1203.
[17] M. P. Fanti, A. M. Mangini, W. Ukovich, A quantized consensus algorithm for
distributed task assignment, in: Decision and Control (CDC), 2012 IEEE 51st 580
Annual Conference on, IEEE, 2012, pp. 2040–2045.
[18] C.-Y. Hsu, B.-R. Kao, K. R. Lai, et al., Agent-based fuzzy constraint-directed ne-
gotiation mechanism for distributed job shop scheduling, Engineering Applications
of Artificial Intelligence 53 (2016) 140–154.
[19] S. Berman,Á. Hal´ asz, M. A. Hsieh, V. Kumar, Optimized stochastic policies for 585
task allocation in swarms of robots, Robotics, IEEE Transactions on 25 (4) (2009)
927–937.
[20] T. W. Mather, M. A. Hsieh, Macroscopic modeling of stochastic deployment poli-
cies with time delays for robot ensembles, The International Journal of Robotics
Research (2011) 0278364911401442.
[21] C. Detrain, J. Pasteels, Caste differences in behavioral thresholds as a ba-
sis for polyethism during food recruitment in the ant, pheidole pallidula
(nyl.)(hymenoptera: Myrmicinae), Journal of insect behavior 4 (2) (1991) 157–176.
[22] N. W. Calderone, R. E. Page Jr, Temporal polyethism and behavioural canalization
in the honey bee, apis mellifera, Animal behaviour 51 (3) (1996) 631–643. 595
[23] K. P. Visscher, R. Dukas, Honey bees recognize development of nestmates’ ovaries,
Animal Behaviour 49 (2) (1995) 542–544.
[24] C. Tofts, Algorithms for task allocation in ants.(a study of temporal polyethism:
theory), Bulletin of Mathematical Biology 55 (5) (1993) 891–918.
[25] E. Bonabeau, G. Theraulaz, J.-L. Deneubourg, Quantitative study of the fixed 600
threshold model for the regulation of division of labour in insect societies, Proceed-
ings of the Royal Society of London. Series B: Biological Sciences 263 (1376) (1996)
1565–1569.
[26] E. Bonabeau, A. Sobkowski, G. Theraulaz, J.-L. Deneubourg, Adaptive task allo-
cation inspired by a model of division of labor in social insects., in: BCEC, 1997, 605
pp. 36–45.
[27] G. Theraulaz, E. Bonabeau, J. Denuebourg, Response threshold reinforcements and
division of labour in insect societies, Proceedings of the Royal Society of London.
Series B: Biological Sciences 265 (1393) (1998) 327–332.
[28] M. Dorigo, G. Caro, L. Gambardella, Ant algorithms for discrete optimization, 610
Artificial life 5 (2) (1999) 137–172.
[29] E. Bonabeau, G. Theraulaz, J.-L. Deneubourg, Fixed response thresholds and the
regulation of division of labor in insect societies, Bulletin of Mathematical Biology
60 (4) (1998) 753–807.
[30] E. L. Mansfield, F. Karayanidis, S. Jamadar, A. Heathcote, B. U. Forstmann, Ad- 615
justments of response threshold during task switching: a model-based functional
magnetic resonance imaging study, The Journal of neuroscience 31 (41) (2011)
14688–14692.
[31] E. Castello, T. Yamamoto, Y. Nakamura, H. Ishiguro, Task allocation for a robotic
swarm based on an adaptive response threshold model, in: Control, Automation 620
and Systems (ICCAS), 2013 13th International Conference on, IEEE, 2013, pp.
259–266.
[32] M.-H. Kim, H. Baik, S. Lee, Response threshold model based uav search planning
and task allocation, Journal of Intelligent & Robotic Systems 75 (3-4) (2014) 625–
640. 625
[33] A. Kanakia, J. Klingner, N. Correll, A response threshold sigmoid function model
for swarm robot collaboration, in: Distributed Autonomous Robotic Systems,
Springer, 2016, pp. 193–206.
[34] W. Lee, D. Kim, History-based response threshold model for division of labor in
multi-agent systems, Sensors 17 (6) (2017) 1232. 630
[35] L. Sundstrom, Sex allocation and colony maintenance in monogyne and polygyne
colonies of formica truncorum (hymenoptera: Formicidae): the impact of kinship
and mating structure, American Naturalist (1995) 182–201.
[36] V. A. Cicirello, S. F. Smith, Wasp-like agents for distributed factory coordination,
Autonomous Agents and Multi-agent systems 8 (3) (2004) 237–266. 635
[37] R. S. Sutton, A. G. Barto, Introduction to reinforcement learning, MIT Press, 1998.
[38] P. Lichocki, D. Tarapore, L. Keller, D. Floreano, Neural networks as mechanisms
to regulate division of labor, The American Naturalist 179 (3) (2012) 391–400.
[39] E. O. Wilson, et al., The insect societies., The insect societies.
[40] M. L. Winston, The biology of the honey bee, Harvard University Press, 1991. 640
[41] Z.-Y. Huang, G. E. Robinson, Regulation of honey bee division of labor by colony
age demography, Behavioral Ecology and Sociobiology 39 (3) (1996) 147–158.
[42] S. N. Beshers, J. H. Fewell, Models of division of labor in social insects, Annual
review of entomology 46 (1) (2001) 413–440.
[43] S. Beshers, Z. Huang, Y. Oono, G. Robinson, Social inhibition and the regulation of 645
temporal polyethism in honey bees, Journal of Theoretical Biology 213 (3) (2001)
461–479.
[44] K. Lerman, C. Jones, A. Galstyan, M. J. Matari´ c, Analysis of dynamic task alloca-
tion in multi-robot systems, The International Journal of Robotics Research 25 (3)
(2006) 225–241. 650
[45] A. Hal´ asz, M. A. Hsieh, S. Berman, V. Kumar, Dynamic redistribution of a swarm
of robots among multiple sites, in: Intelligent Robots and Systems, 2007. IROS
2007. IEEE/RSJ International Conference on, IEEE, 2007, pp. 2320–2325.
[46] M. A. Hsieh,Á. Hal´ asz, S. Berman, V. Kumar, Biologically inspired redistribution
of a swarm of robots among multiple sites, Swarm Intelligence 2 (2) (2008) 121–141.
[47] W. Lee, D. Kim, Adaptive approach to regulate task distribution in swarm
robotic systems, Swarm and Evolutionary Computation BASE DATA (2018), doi: https://doi.org/10.1016/j.swevo.2018.11.005.
[48] Khaluf Y , Vanhee S , Simoens P . Local Ant System for Allocating Robot Swarms to Time-constrained Tasks[J]. Journal of Computational ence, 2018, 31.
[49] Mayya S , Wilson S , Egerstedt M . Closed-loop task allocation in robot swarms using inter-robot encounters[J]. Swarm Intelligence, 2019, 13(2):115-143.
[50] Pang B , Song Y , Zhang C , et al. Autonomous Task Allocation in a Swarm of Foraging Robots: An Approach Based on Response Threshold Sigmoid Model[J]. International Journal of Control Automation & Systems, 2019.
[51] Wei Y , Hiraga M , Ohkura K , et al. Autonomous task allocation by artificial evolution for robotic swarms in complex tasks[J]. Artificial Life & Robotics, 2018.
[52] Yamada K . Autonomous role assignment and task allocation in scalable swarm robotic systems using local interactions[J]. Artificial Life and Robotics, 2018, 23(4):636-644.
[53] Jang I , Shin H S , Tsourdos A , et al. An integrated decision-making framework of a heterogeneous aerial robotic swarm for cooperative tasks with minimum requirements[J]. Proceedings of the Institution of Mechanical Engineers Part G Journal of Aerospace Engineering, 2018:095441001877262.
欢迎大家点赞、评论、收藏、关注~