【NLP】大语言模型基础之Transformer结构_nlp 中的transformer

Transformer是一种深度学习模型架构，由Vaswani等人于2017年在论文《Attention is All You Need》中首次提出。它在自然语言处理（NLP）领域取得了巨大的成功，并被广泛应用于各种任务，如机器翻译、文本摘要、语言建模等。

在Transformer之前，循环神经网络（RNN）和长短时记忆网络（LSTM）等序列模型是处理自然语言数据的主流选择。然而，这些模型存在一些问题，例如难以并行化处理、难以捕捉长距离依赖关系等。Transformer的提出旨在解决这些问题，并通过引入自注意力机制（Self-Attention）实现更高效的序列建模。

从2020年OpenAI发布GPT-3开始，对大语言模型的研究逐渐深入，虽然大语言模型的参数量巨大，通过有监督微调和强化学习能够完成非常多的人物，但是其理论基础仍然是Transformer结构。因此本文将再次回顾Transformer的结构，涉及复杂度、参数设置、上下文学习、Attention方法等。

1. Transformer结构总览

Transformer结构是由谷歌在2017年提出并首先应用于机器翻译的神经网络模型架构。如下图所示，并且标上了序号，方便后面讲解：

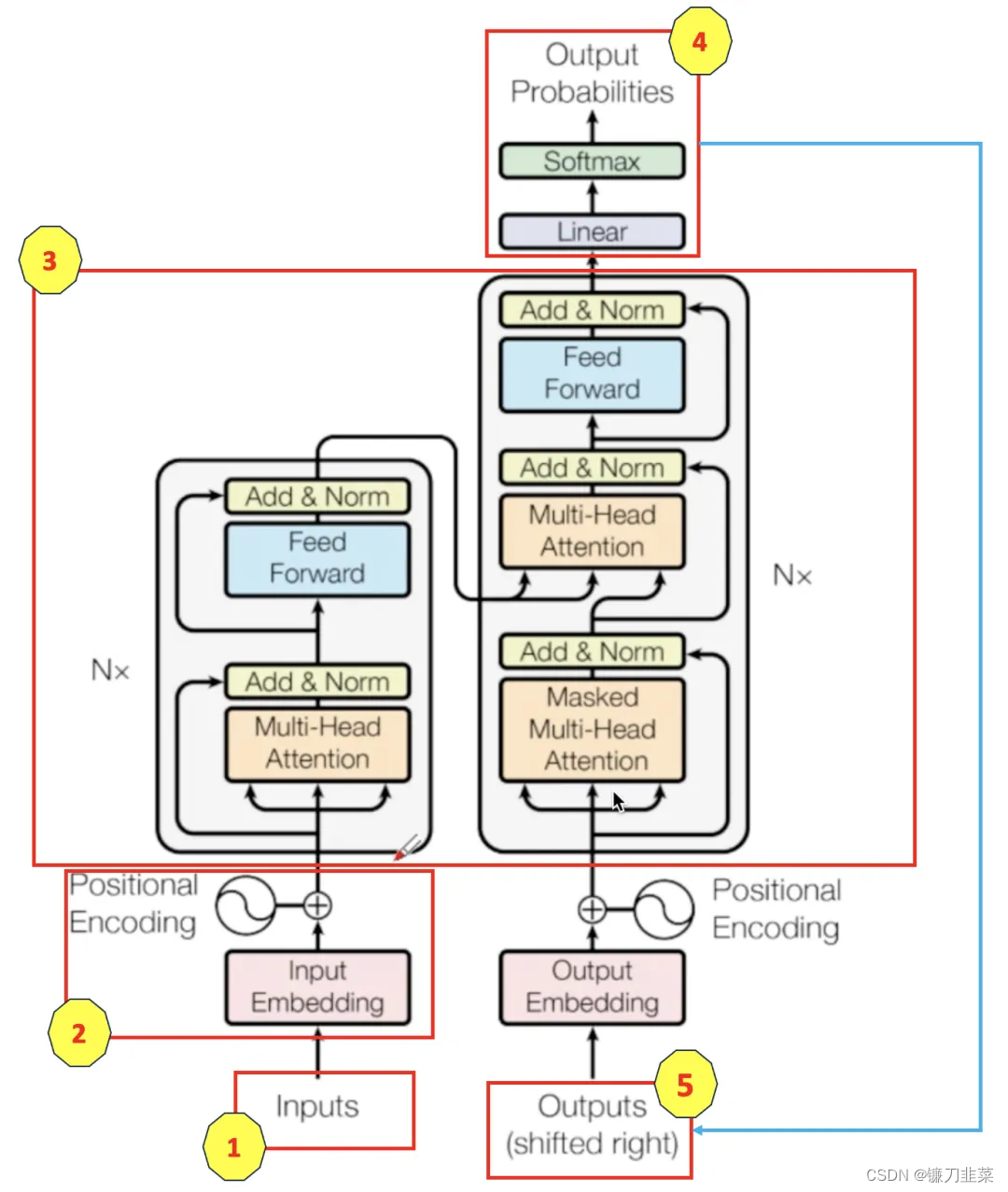
图中(序号3)左侧和右侧分别对应着编码器（Encoder）和解码器（Decoder）结构，它们均由若干个基本的Transformer块(Block)组成。这里的N×表示进行了N次堆叠。每个Transformer块都接收一个向量序列${x_i}_{i=1}^t$作为输入，并输出一个等长的向量序列作为输出${y_i}_{i=1}^t$。这里的$x_i$和$y_i$分别对应文本序列中的一个词元的表示，$y_i$是当前Transformer块对输入$x_i$进一步整合其上下文语义后对应的输出。在从输入${x_i}_{i=1}^t$到输出${y_i}_{i=1}^t$的语义抽象过程中，主要涉及如下几个模块：

• 注意力层：使用多头注意力（Multi-Head Attention）机制整合上下文语义，它使得序列中任意两个单词之间的依赖关系可以直接被建模而不基于传统的循环结构，从而更好地解决文本的长程依赖问题。
  • 它允许模型在不同的表示子空间中学习输入序列的多个关系。
  • 多个自注意力头组合在一起，可以捕获不同类型的信息。
• 位置感知前馈层（Position-wise FFN）:通过全连接层对输入文本序列中的每个单词表示进行更复杂的编码。
  • 位置编码：由于Transformer不像RNN那样天然具有处理序列顺序的能力，因此它通过位置编码（Positional Encoding）来引入序列中元素的位置信息，对应图中序号2。
• 残差链接（Residual Connections）：对应图中Add部分。它是一条分别作用在上述两个子层中的直连通路，被用于连接两个子层的输入和输出，使信息流动更高效，有利于模型的优化。
  • 它允许梯度直接流过每一层，有助于训练深层网络。
• 层归一化（Layer Normalization）：对应图中Norm部分，它作用于上述两个子层的输出表示序列，对表示序列进行层归一化操作，同样起到稳定优化的作用。
  • 用于稳定神经网络的学习过程。

---

补充：什么是tokens？
tokens是分词tokenization的结果，分词就是将句子、段落、文章这类型的长文本，分解为以字词（token）为单位的数据结构。比方说，在句子 “我很开心” 中，利用中文分词得到的列表是{“我”，“很”，“开心”}，列表中的每一个元素代表一个token。对于“ChatGPT is great！”这个字符串，就被编码为6个tokens：“Chat”、“G”、“PT”、“ is”、“ great”、“!”

---

2. 嵌入表示层

对于输入文本序列，先通过输入嵌入层（Input Embedding）将每个单词转换为其相对应的向量表示。通常，直接对每个token创建一个向量表示，在论文中这个向量的大小是d_model=512。由于Transfomer模型不再基于循环的方式建模文本输入，序列中不再有任何信息能够提示来模型输入单词之间的相对位置关系。在送入编码器端建模上下文语义之前，一个非常重要的操作是在词嵌入中加入位置编码(Positional Encoding)这一特征，具体来讲，序列中的每个单词所在的位置都对应一个向量， 位置编码向量 与其 对应的单词表示 相加 然后送入到后续模块中做进一步处理，input如下：
$$\text{input}=\text{input\_embedding}+\text{positional\_encoding}$$
在训练过程中，模型会自动学习到如何利用这部分的位置信息。Transformer 模型使用不同频率的正余弦函数计算位置编码：
$$PE(pos，2i)=sin(\frac{pos}{10000^{\frac{2i}{d}}})$$
$$PE(pos,2i+1)=cos(\frac{pos}{10000^{\frac{2i}{d}}})$$
其中pos表示单词所在的位置， $2i$和$2i+1$表示位置编码向量中的对应维度，d表示对应位置编码的总维度(d_model=512)。

使用正余弦做位置编码的好处：

1. 正余弦函数的范围在[-1, 1]，导出的位置编码与原词嵌入（input_embedding）相加不会使得结果偏离过大而对词义产生破坏；
2. 依据三角函数的性质，可以得知第pos+k个位置的编码是第pos个位置的编码的线性组合，这就意味着位置编码中蕴含着单词之间的距离信息。
   关于以上第2点的理解，论文里面的解释如下，使用正余弦交替的位置编码，有以下2个特性：

Property 1. For an offset k and a position t, $P{E}_{t+k}^{T}P{E}_t$ only depends on k, which means the dot product of two sinusoidal position embeddings can reflect the distance between two tokens.

特性1：对于一个偏移k和一个位置t来说， $P{E}_{t+k}^{T}P{E}_t$ 的结果仅仅和偏移k有关系，这意味着两个正弦位置嵌入的点乘可以反应两个tokens的距离。

Property 2. For an offset k and a position t, $P{E}_t^{T}P{E}_{t-k}=P{E}_t^{T}P{E}_{t+k}$, which means the sinusoidal position embeddings is unware of directionality.

特性2: 对于一个偏移k和一个位置t， $P{E}_t^{T}P{E}_{t-k}=P{E}_t^{T}P{E}_{t+k}$，这意味着tokens的正弦位置嵌入不具有方向性。

使用PyTorch实现的位置编码如下：

import math
import torch
import torch.nn as nn
import torch.nn.functional as F

from torch.autograd import Variable


class PositionalEncoder(nn.Module):
    def __init__(self, d_model, max_seq_len=80):
        super().__init__()
        self.d_model = d_model
        # 根据pos和i创建一个常量PE矩阵
        pe = torch.zeros(max_seq_len, d_model)
        for pos in range(max_seq_len):
            for i in range(0, d_model, 2):
                pe[pos, i] = math.sin(pos / (10000 ** (i / d_model)))
                pe[pos, i + 1] = math.cos(pos / (10000 ** (i / d_model)))

        pe = pe.unsqueeze(0)
        self.register_buffer('pe', pe)

    def forward(self, x):
        # 使得单词嵌入表示相对大一些
        x = x * math.sqrt(self.d_model)
        # 增加位置常量到单词嵌入表示中
        seq_len = x.size(1)
        x = x + Variable(self.pe[:, :seq_len], requires_grad=False).cuda()
        return x
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

2. 注意力层

自注意力（Self-Attention）操作是基于Transformer的机器翻译模型的基本操作，在源语言的编码和目标语言的生成中频繁地被使用以建模源语言、目标语言任意两个单词之间的依赖关系。

给定输入，对于每个tokens，它的输入是:$$x=\text{input\_embedding}(单词语义嵌入)+\text{positional\_encoding}(位置编码)$$
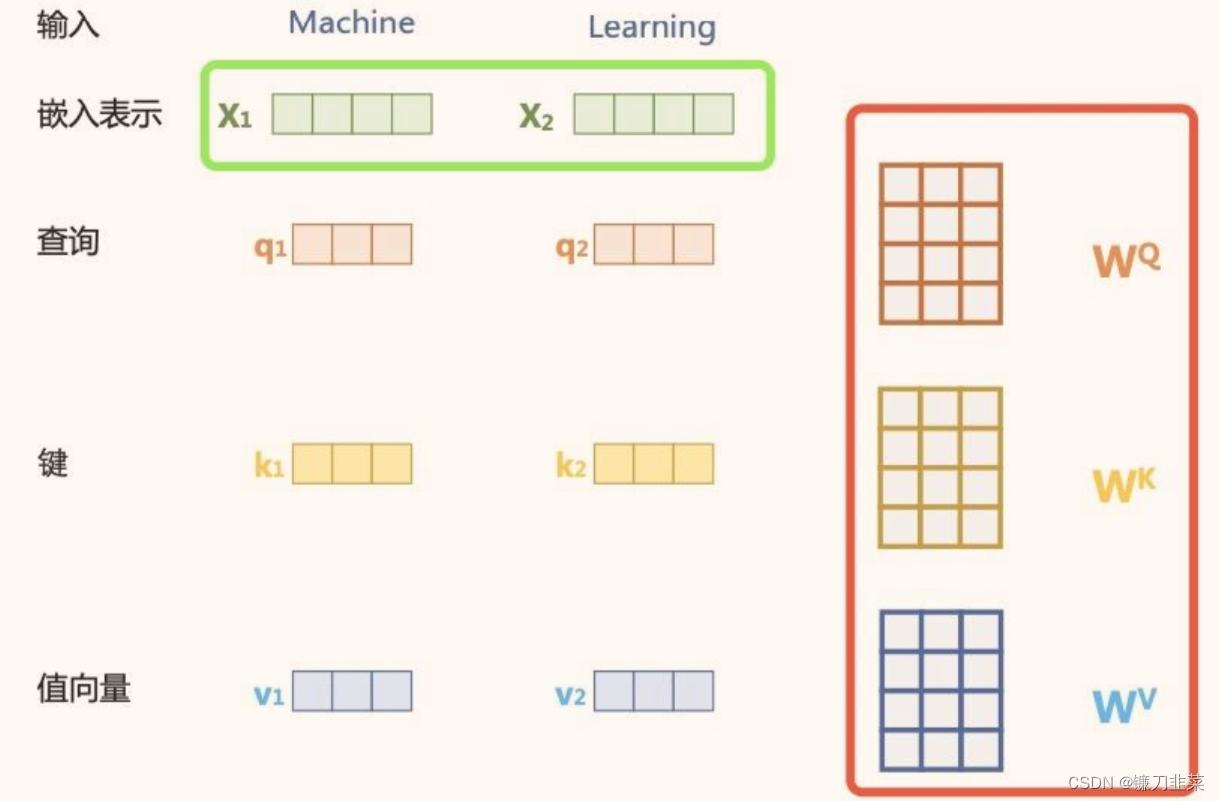
每一项都是d维的，有d_model参数决定；输入表示为 { x i ∈ R d } i = 1 t \{x_i\in \mathcal{R}^d\}_{i=1}^t {xi​∈Rd}i=1t​，为了实现对 上下文语义依赖的建模，引入自注意力机制，涉及到Self-Attention机制中的三个元素及其对应的矩阵：

• query: $q_i(Query);W^Q\in R^{d\ast d_q}$
• key：$k_i(Key);W^K\in R^{d\ast d_k}$
• value：$v_i(Value);W^V\in R^{d\ast d_v}$

在编码输入序列中每一个单词的表示过程中，这三个元素用于计算上下文单词所对应的权重得分，这些权重反映了在编码当前单词的时候，对于上下文不同部分所需要的关注程度。具体来说，通过三个线性变换$W^Q\in R^{d\ast d_q}$,$W^K\in R^{d\ast d_k}$,$W^V\in R^{d\ast d_v}$将输入序列中的每一个token对应的表示$x_i$转换对应的$q_i\in R^{d_q}$，$k_i\in R^{d_k}$，$v_i\in R^{d_v}$向量。

针对当前token获取上下文关注权重的计算：在编码token$x_i$的时候，为了获得所需要关注的上下文信息，首先通过$q_i$和其他位置的键向量做点积得到匹配分数$q_i\cdot k_1,q_i\cdot k_2,...,q_i\cdot k_t$。为了防止匹配的权重在后续Softmax计算过程中导致梯度爆炸以及收敛效率差的问题，这些得分会除以放缩因子$\sqrt{d}$以稳定优化。放缩后的得分经过Softmax归一化为概率，与其他位置的值向量相乘来聚合希望关注的上下文信息，并且最小化不相关的干扰信息：
$$Z=\text{Attention}(Q,K,V)=\text{Softmax}(\frac{Q{K}^T}{\sqrt{d}})V$$
其中$Q\in R^{L\ast d_q}，K\in R^{L\ast d_k}，V\in R^{L\ast d_v}$, L表示序列长度，$Z\in R^{L\ast d_v}$表示自注意力操作的输出。
多头自注意力（Multi-head Attention）机制：为了进一步增强自注意力机制 聚合上下文信息的能力，提出了Multi-head Attention机制，用来关注上下文的不同侧面。具体来说，上下文中的每一个单词的表示$x_i$经过多组线性KaTeX parse error: Expected 'EOF', got '}' at position 22: …Q,W_j^K,W_j^V\\}̲_{j=1}^N映射到不同的表示子空间中，即每个token的输入$x_i$经过多组线性变化 { W j Q , W j K , W j V } j = 1 N \{W_j^Q,W_j^K,W_j^V\}_{j=1}^N {WjQ​,WjK​,WjV​}j=1N​映射到不同的 { Z j } j = 1 N \{Z_j\}_{j=1}^N {Zj​}j=1N​。最终使用线性变化 W O ∈ { R ( N d v ) ∗ d } W^O\in \{R^{(N_{d_v})*d}\} WO∈{R(Ndv​​)∗d}用于综合不同子空间的上下文表示并形成自注意力层最终的输出 { x i ∈ R d } i = 1 t \{x_i\in R^d\}_{i=1}^t {xi​∈Rd}i=1t​。

使用PyTorch实现的自注意力层代码如下：

import copy
import numpy as np
from typing import Optional, Any, Union, Callable
from torch import Tensor


class MultiHeadAttention(nn.Module):
    def __init__(self, num_heads: int, d_model: int, dropout: float = 0.1):
        super(MultiHeadAttention, self).__init__()
        assert d_model % num_heads == 0, "d_model must be divisible by num_heads"
        self.d_model = d_model
        self.k_dim = d_model // num_heads
        self.num_heads = num_heads

        # self.q_linear = nn.Linear(d_model, d_model)
        # self.v_linear = nn.Linear(d_model, d_model)
        # self.k_linear = nn.Linear(d_model, d_model)
        # self.out = nn.Linear(d_model, d_model)
        self.proj_weights = clones(nn.Linear(d_model, d_model), 4)  # W^Q, W^K, W^V, W^O

        self.attention_score = None
        self.dropout = nn.Dropout(p=dropout)

    def forward(self, query: Tensor, key: Tensor, value: Tensor, mask: Optional[Tensor] = None):
        """
        Args:
            query: shape (batch_size, seq_len, d_model)
            key: shape (batch_size, seq_len, d_model)
            value: shape (batch_size, seq_len, d_model)
            mask: shape (batch_size, seq_len, seq_len). Since we assume all data use a same mask, so
                  here the shape also equals to (1, seq_len, seq_len)

        Return:
            out: shape (batch_size, seq_len, d_model). The output of a multi_head attention layer
        """
        if mask is not None:
            mask = mask.unsqueeze(1)
        batch_size = query.size(0)
        # # 利用线性计算划分出h个头
        # query = self.q_linear(query).view(batch_size, -1, self.num_heads, self.k_dim)
        # key = self.k_linear(key).view(batch_size, -1, self.num_heads, self.k_dim)
        # value = self.v_linear(value).view(batch_size, -1, self.num_heads, self.k_dim)
        # # 矩阵转置
        # query = query.transpose(1, 2)
        # key = key.transpose(1, 2)
        # value = value.transpose(1, 2)

        # 1) Apply W^Q, W^K, W^V to generate new query, key, value
        query, key, value = [proj_weight(x).view(batch_size, -1, self.num_heads, self.k_dim).transpose(1, 2)
                             for proj_weight, x in zip(self.proj_weights, [query, key, value])]  # -1 equals to seq_len

        # # 计算attention
        # scores = attention(query, key, value, mask, self.dropout)
        # # 连接多个头并输入最后的线性层
        # concat = scores.transpose(1,2).contiguous().view(batch_size, -1, self.d_model)

        # 2) Calculate attention score and the out
        out, self.attention_score = attention(query, key, value, mask=mask, dropout=self.dropout)

        # 3) "Concat" output
        out = out.transpose(1, 2).contiguous().view(batch_size, -1, self.num_heads * self.k_dim)
        # output = self.out(concat)

        # 4) Apply W^O to get the final output
        output = self.proj_weights[-1](out)
        return output


def clones(module, N):
    """Produce N identical layers."""
    return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])


def attention(query: Tensor, key: Tensor, value: Tensor, mask: Optional[Tensor] = None, dropout: float = 0.1):
    """
    Define how to calculate attention score
    Args:
        query: shape (batch_size, num_heads, seq_len, k_dim)
        key: shape(batch_size, num_heads, seq_len, k_dim)
        value: shape(batch_size, num_heads, seq_len, v_dim)
        mask: shape (batch_size, num_heads, seq_len, seq_len). Since our assumption, here the shape is
              (1, 1, seq_len, seq_len)
    Return:
        out: shape (batch_size, v_dim). Output of an attention head.
        attention_score: shape (seq_len, seq_len).

    """
    k_dim = query.size(-1)
    # shape (seq_len ,seq_len)，row: token，col: that token's attention score
    scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(k_dim)
    # 掩盖那些为了填补长度而增加的单元，使其通过Softmax计算后为0
    if mask is not None:
        mask = mask.unsqueeze(1)
        scores = scores.masked_fill(mask == 0, -1e9)

    attention_score  = F.softmax(scores, dim=-1)
    if dropout is not None:
        attention_score  = dropout(attention_score )
    output = torch.matmul(scores, value)
    return output, attention_score    # shape: (seq_len, v_dim), (seq_len, seq_lem)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100

3. 前馈层

前馈层接收自注意力子层的输出作为输入，并通过一个带有ReLU激活函数的两层全连接网络对输入进行更复杂的非线性变换。这一非线性变换会对模型最终的性能产生重要的影响。$$FFN(x)=ReLU(x{W}_1+b_1)W_2+b_2$$
其中$W_1,b_1,W_2,b_2$表示前馈子层的参数。结果表明，增大前馈子层隐状态的维度有利于提高最终翻译结果的质量，因此，前馈子层隐状态的维度一般比自注意力子层要大。
使用PyTorch实现的前馈层的代码：

class FeedForward(nn.Module):
    def __init__(self, d_model, d_ff=2048, dropout=0.1):
        super(FeedForward, self).__init__()
        # d_ff默认设置为2048
        self.linear_1 = nn.Linear(d_model, d_ff)
        self.dropout = nn.Dropout(dropout)
        self.linear_2 = nn.Linear(d_ff, d_model)

    def forward(self, x):
        x = self.dropout(F.relu(self.linear_1(x)))
        x = self.linear_2(x)
        return x
1
2
3
4
5
6
7
8
9
10
11
12

4. 残差连接与层归一化

由Transformer结构组成的网络结构通常都非常大。编码器和解码器均由很多层基本的Transformer块组成，每一层中都包含复杂的非线性映射，这就导致模型的训练比较困难。因此，需要在Transformer块中进一步引入了残差连接与层归一化技术，以进一步提升训练的稳定性。

具体来说，残差连接主要是使用一条直连通道直接将对应子层的输入连接到输出，避免在优化过程中因网络过深而产生潜在的梯度消失问题：$$x^{l+1}=f(x^l)+x^l$$
其中$x^l$表示第$l$层的输入，$f(\cdot )$表示一个映射函数。此外，为了使每一层的输入/输出稳定在一个合理的范围内，层归一化技术被进一步引入每个Transformer块中：
$$LN(x)=\alpha \cdot \frac{x-\mu }{\sigma }+b$$
其中$\mu$和$\sigma$分别表示均值和方差，用于将数据平移缩放到均值为0，方差为1的标准分布，$\alpha$和$\beta$是可学习的参数。层归一化技术可以有效地缓解优化过程中潜在的不稳定、收敛速度慢等问题。

使用PyTorch实现的层归一化代码如下：

class Norm(nn.Module):
    def __init__(self, d_model, eps=1e-6):
        super(Norm, self).__init__()
        self.size = d_model
        # 层归一化包含两个可以学习的参数
        self.alpha = nn.Parameter(torch.ones(self.size))
        self.blas = nn.Parameter(torch.zeros(self.size))

        self.eps = eps  # 用于数值稳定性的分母小值

    def forward(self, x):
        norm = self.alpha * (x - x.mean(dim=-1, keepdim=True)) / (x.std(dim=-1, keepdim=True) + self.eps) + self.bias
        return norm
1
2
3
4
5
6
7
8
9
10
11
12
13

5. 编码器和解码器结构

基于上述模块，根据图中给出的网络结构，编码器端较容易实现。但是解码器端更为复杂。具体来说，解码器的每个Transformer块的第一个自注意力子层额外增加了注意力掩码，对应图中的掩码多头注意力（Masked Multi-Head Attention）部分，这主要是因为在翻译的过程中，编码器端主要用于编码源语言序列的信息，而这个序列是完全已知的，因而编码器仅需要考虑如何融合上下文语义信息。解码器端则负责生成目标语言序列，这一生成过程是自回归的，即对于每一个单词的生成过程，仅有当前单词之前的目标语言序列是可以被观测的，因此这一额外增加的掩码是用来掩盖后续的文本信息的，以防模型在训练阶段直接看到后续的文本序列，进而无法得到有效的训练。

此外，解码器端额外增加了一个多头交叉注意力（Multi-Head Cross-Attention）模块，使用交叉注意力（Cross-Attention）方法，同时接收来自编码器端的输出和当前Transformer块的前一个掩码注意力层的输出。Query是通过解码器前一层的输出进行投影的，Key和Value是使用编码器的输出进行投影的。它的作用是在翻译的过程中，为了生成合理的目标语言序列，观测待翻译的源语言序列是什么。基于上述编码器和解码器结构，待翻译的源语言文本，经过编码器端的每个Transformer块对其上下文语义进行层层抽象，最终输出每一个源语言单词上下文相关的表示。

解码器端以自回归的方式生成目标语言文本，即在每个时间步$t$，根据编码器输出的源语言文本表示，以及前$t-1$个时刻生成的目标语言文本，生成当前时刻的目标语言单词。

使用PyTorch实现的编码器代码：

class EncoderLayer(nn.Module):
    def __init__(self, d_model, num_heads, dropout=0.1):
        super(EncoderLayer, self).__init__()
        self.norm1 = Norm(d_model)
        self.norm2 = Norm(d_model)
        self.attn = MultiHeadAttention(num_heads, d_model, dropout=dropout)
        self.ff = FeedForward(d_model, dropout=dropout)
        self.dropout1 = nn.Dropout(dropout)
        self.dropout2 = nn.Dropout(dropout)

    def forward(self, x, mask):
        attn_output = self.attn(x, x, x, mask)
        attn_output = self.dropout_1(attn_output)
        x = x + attn_output
        x = self.norm1(x)
        ff_output = self.ff(x)
        ff_output = self.dropout2(ff_output)
        x = x + ff_output
        x = self.norm2(x)
        return x

class Encoder(nn.Module):
    def __init__(self, src_vocab_size, d_model, N, num_heads, dropout):
        super(Encoder, self).__init__()
        self.N = N
        self.src_emb = nn.Embedding(src_vocab_size, d_model)
        self.pe = PositionalEncoder(d_model)
        self.layers = nn.ModuleList([EncoderLayer(d_model, num_heads, dropout) for _ in range(N)])
        self.norm = Norm(d_model)

    def forward(self, src, mask):
        x = self.embed(src)
        x = self.pe(x)
        for i in range(self.N):
            x = self.layers[i](x, mask)
        return self.norm(x)

class DecoderLayer(nn.Module):
    def __init__(self, d_model, num_heads, dropout=0.1):
        super(DecoderLayer, self).__init__()
        self.norm_1 = Norm(d_model)
        self.norm_2 = Norm(d_model)
        self.norm_3 = Norm(d_model)

        self.dropout_1 = nn.Dropout(dropout)
        self.dropout_2 = nn.Dropout(dropout)
        self.dropout_3 = nn.Dropout(dropout)

        self.attn_1 = MultiHeadAttention(num_heads, d_model, dropout=dropout)
        self.attn_2 = MultiHeadAttention(num_heads, d_model, dropout=dropout)
        self.ff = FeedForward(d_model, dropout=dropout)

    def forward(self, x, e_outputs, src_mask, trg_mask):
        attn_output_1 = self.attn_1(x, x, x, trg_mask)
        attn_output_2 = self.dropout_1(attn_output_1)
        x = x + attn_output_1
        x = self.norm_1(x)
        attn_output_2 = self.attn_2(x, e_outputs, e_outputs, src_mask)
        attn_output_2 = self.dropout_2(attn_output_2)
        x = x + attn_output_2
        x = self.norm_2(x)

        ff_output = self.ff(x)
        ff_output = self.dropout_3(ff_output)

        x = x + ff_output
        x = self.norm_3(x)
        return x

class Decoder(nn.Module):
    def __init__(self, vocab_size, d_model, N, num_heads, dropout):
        super(Decoder, self).__init__()
        self.embed = nn.Embedding(vocab_size, d_model)
        self.pe = PositionalEncoder(d_model)
        self.layers = nn.ModuleList([DecoderLayer(d_model, num_heads, dropout) for _ in range(N)])
        self.norm = Norm(d_model)

    def forward(self, trg, e_outputs, src_mask, trg_mask):
        x = self.embed(trg)
        x = self.pe(x)
        for i in range(self.N):
            x = self.layers[i](x, e_outputs, src_mask, trg_mask)
        return self.norm(x)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83

完整代码可参考相关链接大规模语言模型：从理论到实践

参考文献

1. 模型结构简介以及位置编码Positional Encoding
2. 新手深入浅出理解PyTorch归一化层全解析
3. encoder（编码器）和decoder（解码器）
4. Transformer的模型和代码解析