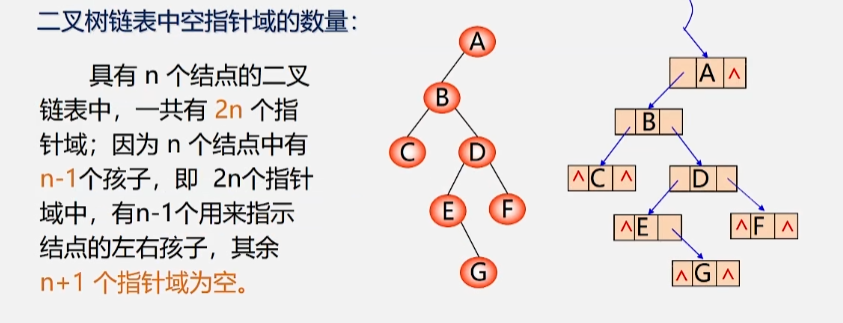
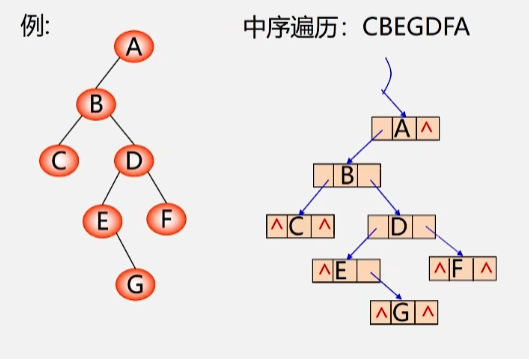
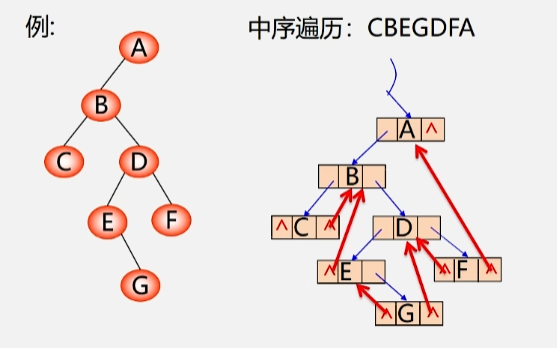
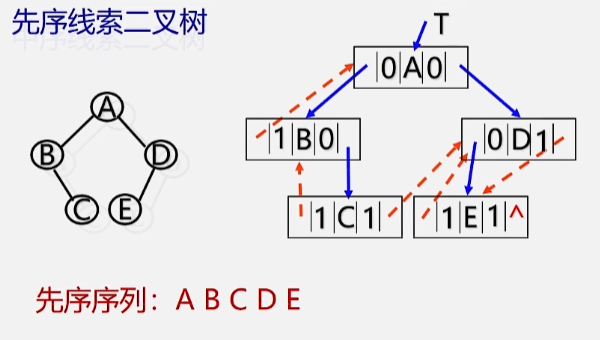
- 1ASP.NET Core 教学 - Web API JSON 序列化设定
- 2关于Android日历视图控件CalendarView
- 3Unity3D-高通AR-《狼来了》-3识图卡AR场景_unity ar场景
- 4magento webapi 接口返回 json对象_webapi返回json数据
- 5【MySQL数据库】如何指定SQL查询使用特定的索引?_指定索引
- 6CONVERT 转换函数的简单使用方法_convert函数
- 7【人工智能基础】聚类实验分析
- 8堆的定义,堆与树的区别,堆排序(Java实现)_堆和树的区别
- 9m3u8手机批量转码_M3U8批量转换器(Android)开发
- 10国际市场营销学试卷题(分章打印复习题)
【数据结构(23)】5.5 遍历二叉树和线索二叉树_1.先序遍历的顺序创建二叉链表。 问题分析 算法描述 运行结果
赞
踩
一、遍历二叉树
遍历定义
- 顺着某一条搜索路径巡访二叉树中的每个结点,使得每个结点均被访问依次,而且仅被访问一次(又称周游)。
- “访问” 的含义很广,可以是对结点作各种处理.
- 如:输出结点的信息,修改结点的数据值等,但是要求这种访问不能破坏原来的数据结构。
- 如:数组的遍历就是从第一个元素一直访问到最后一个元素,此处输出数组内的每个值。
int a[5]={1,2,3,4,5};
int i;
for(i = 0;i < 5;i++ )
{
printf("%d ",a[i]);
//依次访问数组中的每个元素,就叫遍历。
}
return 0;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
1 2 3 4 5
- 1
遍历目的
- 得到树中所有结点的一个线性排列。
- 这样一棵二叉树的每个结点是有分支的,访问完一个结点之后,再去访问下一个,下一个结点又是哪一个呢,此时就需要确定一个顺序,要把树这样一个非线性结构变成一个线性排列。
遍历用途
- 它是树结构插入、删除、修改、查找和排序运算的前提,是二叉树一切运算的基础和核心。所以,二叉树的遍历是本章的重中之重。
1. 遍历二叉树算法描述
遍历方法
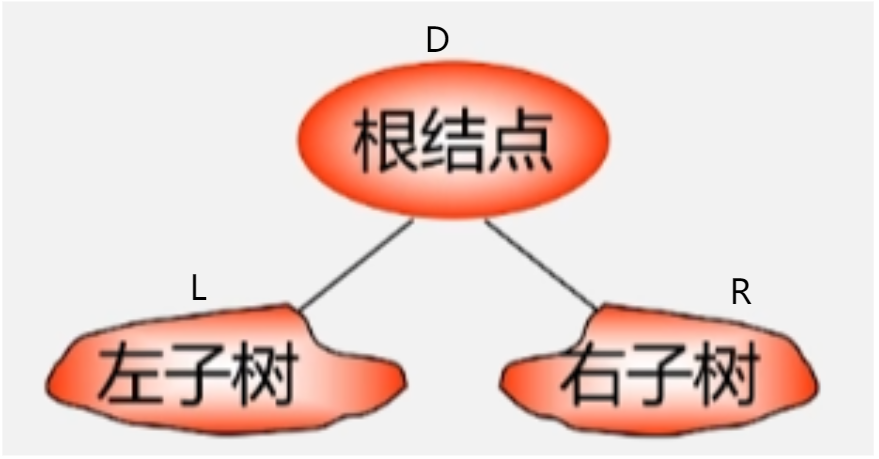
- 回顾二叉树的递归定义可知,二叉树是由 3 个基本单位构成的:根节点、左子树和右子树。若能依次遍历这三部分,就是遍历了整个二叉树。
- 假设:L:遍历左子树,D:访问根结点,R:遍历右子树。则可以有 DLR、LDR、LRD、DRL、RDL、RLD 这 6 种遍历二叉树的方案。
- 若规定先左后右,则只有前三种情况:
- DLR——先(根)序遍历。
- LDR——中(根)序遍历。
- LRD——后(根)序遍历。
- 第一个访问根结点就称为先序遍历,第二个访问根节点称为中序遍历,后序遍历同理。
- 若规定先左后右,则只有前三种情况:
算法描述
- 由二叉树的递归定义可知,遍历左子树和遍历右子树可如同遍历二叉树一样 递归 进行。
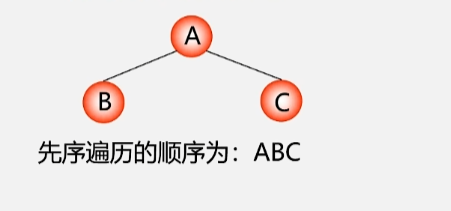
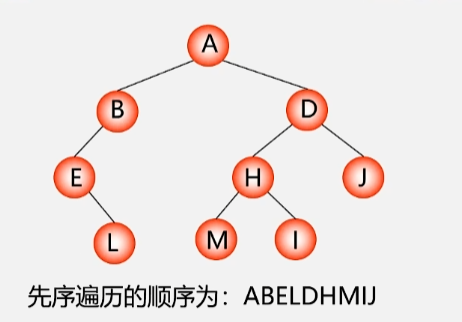
1.1 先序遍历二叉树
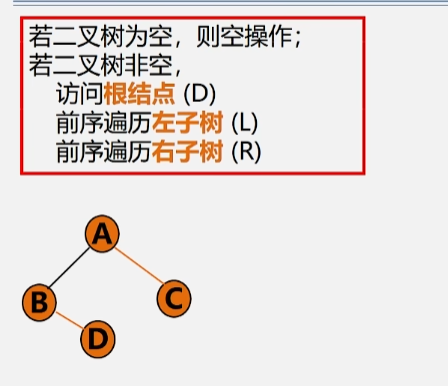
若二叉树为空,则空操作;否则执行以下操作:
- 访问根结点
- 先序遍历左子树
- 先序遍历右子树
牢记按照 根左右 的顺序来进行遍历。每个结点的左子树的所有结点遍历完了之后才能轮到右子树。当一个结点的左右子树都为空的时候表示访问完毕。
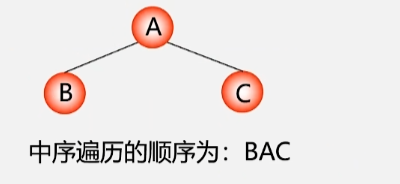
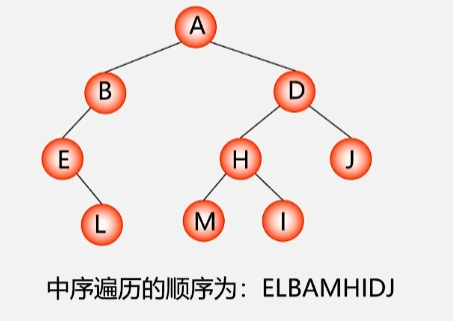
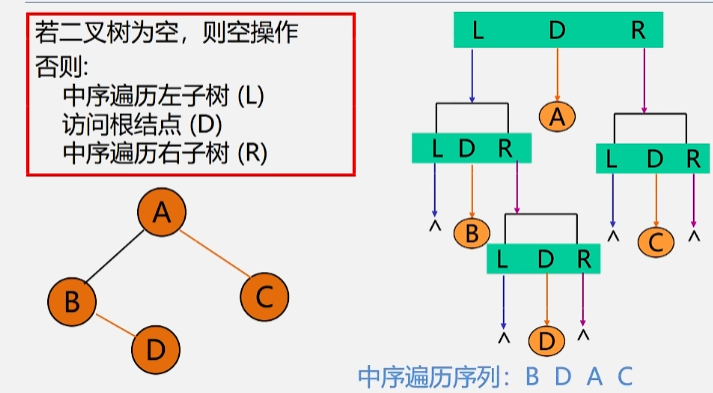
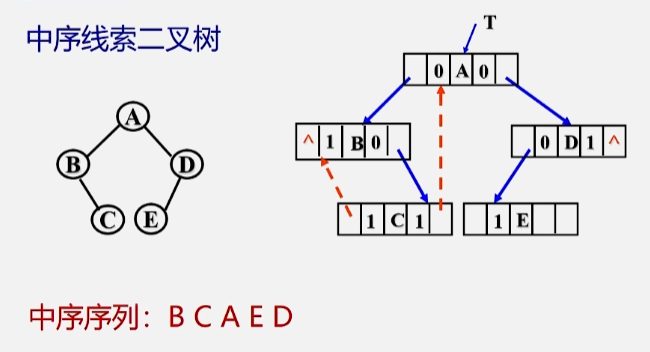
1.2 中序遍历二叉树
- 按照 左根右 的顺序进行遍历,根节点之下的每一棵二叉树都按照左根右的顺序遍历。
- 左子树按照 左根右 的顺序访问完所有结点之后才能访问根结点,最后右子树同样按照 左根右 的顺序访问所有结点。
若二叉树为空,则空操作;否则执行以下操作:
- 中序遍历左子树。
- 访问根结点。
- 中序遍历右子树。
每个结点的左子树按照左根右的顺序访问完了之后,才能访问根结点,最后按照 左根右 的顺序访问该结点的右子树的所有结点。
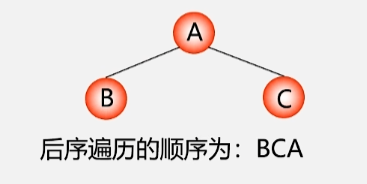
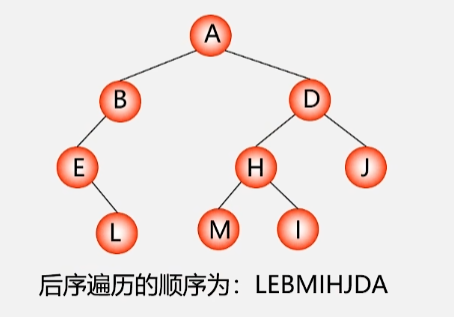
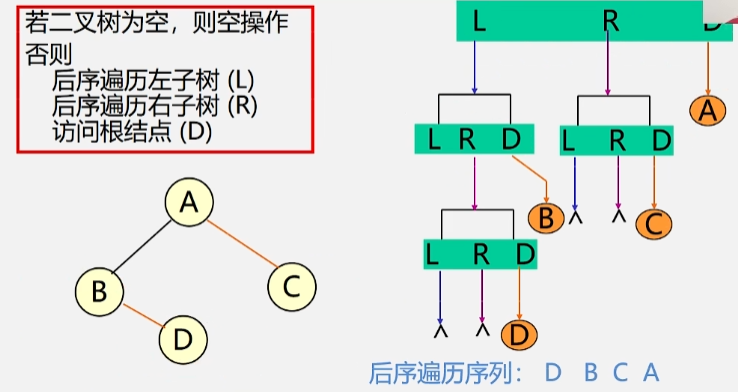
1.3 后序遍历二叉树
每个结点都按照左右根的顺序访问结点,每个结点的左子树按照左右根的顺序访问完所有结点之后,再到该结点的右子树按照左右根的顺序访问所有结点,最后访问该结点。
若二叉树为空,则空操作;否则执行以下操作:
- 后序遍历左子树。
- 后序遍历右子树。
- 访问根结点。
1.4 遍历二叉树例题
将所有非叶子结点看成根结点,然后按照各种每种遍历顺序进行遍历,就很轻松了。
【例1】
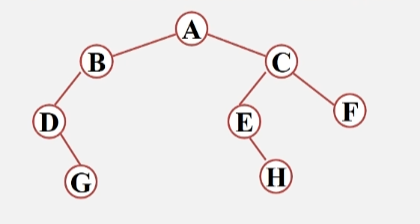
- 写出下图二叉树的各种遍历顺序。
- 先序遍历:ABDG CEHF
- 中序遍历:DGBA EHCF
- 后序遍历:GDBH EFCA
【例2】
- 用二叉树表示算术表达式
- 请写出下图所示二叉树的各种遍历顺序。
- 先序遍历的表达式称为:前缀表达式(波兰式)。
- 中序遍历的表达式称为:中缀表达式。
- 后序遍历的表达式称为:后缀表达式(逆波兰式)。
- 以后如果遇到要求将中缀表达式转换成后缀表达式的,就是将二叉树的中序遍历变成后序遍历。
2. 根据遍历序列确定二叉树
- 若二叉树中各结点的值均不相同,则二叉树结点的先序序列、中序序列和后序序列都是唯一的。
- 由二叉树的先序序列和中序序列,或者由二叉树的后序序列和中序序列可以确定唯一一棵二叉树。
- 由先序序列和后序序列不能确定一棵树的原因是,不能确定哪个结点是根。
2.1 已知先序和中序序列求二叉树
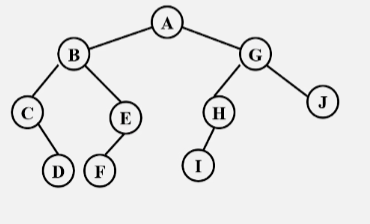
已知二叉树的先序和中序序列,构造出相应的二叉树。
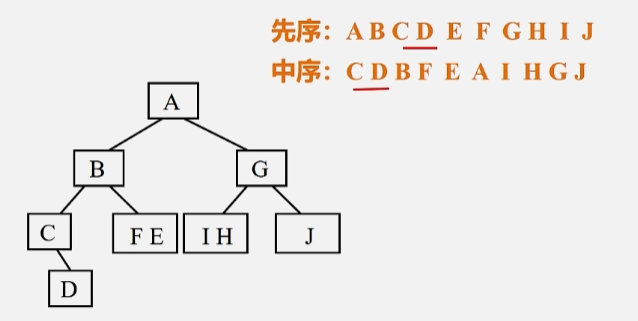
- 先序(根左右):A B C D E F G H I J
- 中序(左根右):C D B F E A I H G J
- 对于一棵大树来说,先序遍历的第一个结点 A 肯定就是根节点。
- 在中序遍历中找到根结点 A 了之后,就能确定,根节点 A 左边的结点 CDBFE,一定在左子树上,右子树同理为 IHGJ。
- 左子树按照先序排列的话第一个结点 B 一定是根。
- 同理,知道 B 是根的话,按照中序 B 左边的结点一定在 B 的左子树位置,FE 则在 B 的右子树位置。
- 同理,按照先序排列 A 的右子树的第一个结点就是G,G 左边的结点 HI 为左子树,J 为 G 的右子树。
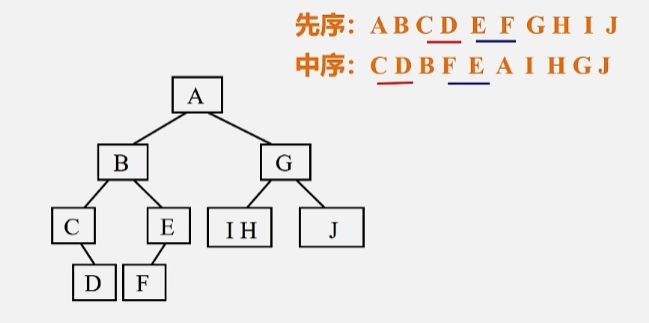
- 按照先序来看,对于 CD 来说,C 在前面,所以 C 是根,又按照中序看,D 在根 C 的后面(右边),所以 D 为 C 的右子树。
- 同理,由 FE 构成的树
- 按先序看,E 在前,所以 E 为根。
- 按中序看,F 在根 E 的前面,所以 F 在 E 的左子树。
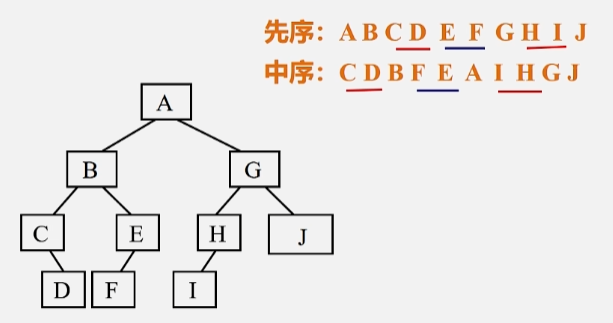
- 在 HI 这棵子树上,
- 由先序看:H 在前,所以 H 为根。
- 有中序看:I 在前,所以 I 为 H 的左子树
最后就剩个 J 结点,所以不用再往后分了。
至此,这棵二叉树构造完成。
2.2 已知中序序列和后序序列求二叉树
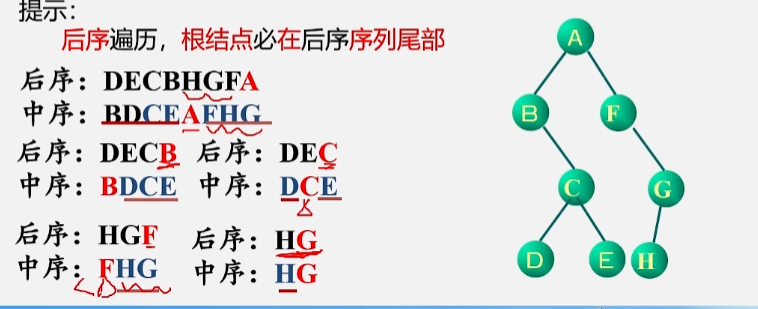
已知一棵二叉树的中序和后序序列,请画出这棵二叉树。
- 中序(左根右)序列:B D C E A F H G
- 后序(左右根)序列:D E C B H G F A
- 由后序遍历可知,最后一个结点 A 一定是整棵树的根节点。
- 中序当中,知道 A 是根的话,那么 A 左边的结点 BDCE 就是左子树,右子树就是 FHG。
- 由中序(左根右)可知,第一个结点 B 一定是左子树的根,由后序(左右根)可知,找到结点B,B 结点左边的结点 DEC,就是以 B 为根的这棵树底下的所有结点。
- 由中序判断 DCE 都在 B 的右子树上,在后序中又能判断出 C 是 B 的右子树的根,由中序判断根 C 的左、右子树分别是 D、E。
- 由后序知,右子树的根是F,由中序知,HG 在根 F 的后边(左根右,在根的后边的肯定都在右子树上),此时就剩个 HG了,由后序可知,G 在 H 的后面,说明 G 为根,且由中序判断,H 在 G 的左边,说明 H 是 G 的左子树。
3. 二叉树遍历的算法实现
- 二叉树的定义实际是个递归的定义,二叉树的左、右子树任然是二叉树。
- 如果能够遍历一棵二叉树的话,在遍历它的左、右子树的时候,仍采用和遍历二叉树时相同的方法。
- 如:如果用先序来遍历一棵二叉树,那么这棵二叉树下的每个子树都能采用这个方法。
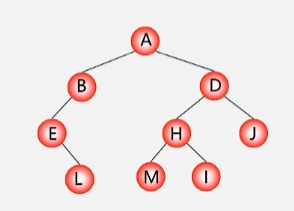
举个栗子
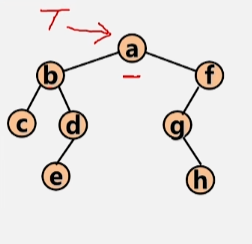
- 按照先序遍历的方式访问上图这棵树,首先访问它的根节点A。
- 然后去遍历它的左子树B(左子树按照同样的方式遍历),如果左子树不为空,先访问它的根结点 B,然后左子树,然后右子树。
- 此时以B为结点的左子树就访问完毕了。
- 左子树访问完毕之后就到右子树了,遍历方法同大二叉树的一致。
- 先访问右子树的根 C,然后访问 C 的左子树为空,最后再访问 C 的右子树,也为空,此时访问结束。
3.1 先序遍历
算法步骤
- 先访问这棵树的根节点 T 。
- 然后用同样的方法去递归访问左子树,将左子树的根结点T ->lchild 传给函数PreOrderTraverse。
- 当子树的某个结点为空的时候,返回上一层。
- 当左子树遍历完毕的时候,然后再继续递归遍历右子树。
执行过程
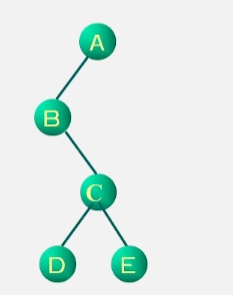
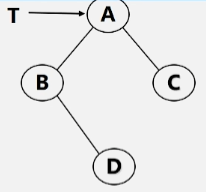
假设有这么一棵二叉树,指针 T 指向二叉树的根节点 A 。对以A为根的二叉树进行遍历。
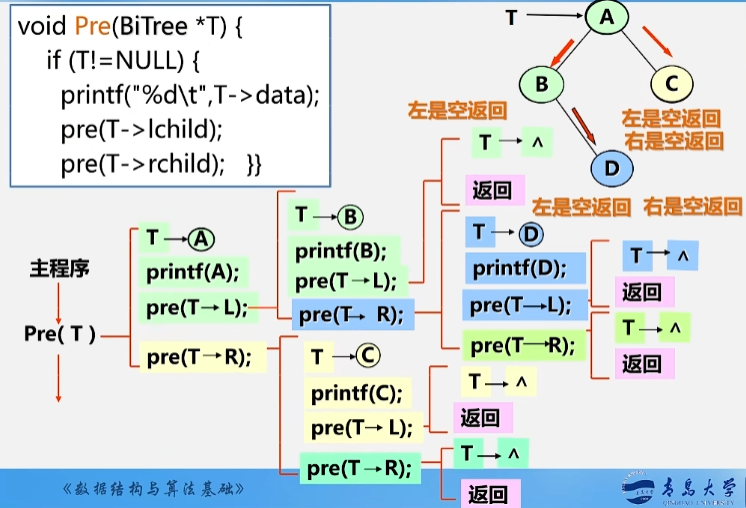
//前趋(先序)遍历
void Pre(BiTree* T)
{
//二叉树及二叉树底下的所有子树中,
//某一棵树不为空时,执行以下操作
if(T != NULL)
{
printf("%d\n",T -> data);
//输出根节点的值
pre(T -> lchile);
//以同样的先序遍历的方法遍历左子树
pre(T -> rchile);
//以同样的先序遍历的方法遍历右子树
//当左、右子树的某个结点为空时,
//返回该结点的递归的上一层
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 反复的执行根左右的顺序,遍历每个小树。
- 当有不为空的树时,就得执行根左右。
- 这样一层一层的深入,当执行完毕的时候再一层一层的返回。
- 直到第一次调用的根左右执行完毕的时候,才返回到主函数。
先序序列:A B D C
- 有了二叉树的先序遍历算法之后,中序以及后序算法起始也差不多了。
3.2 中序遍历
3.3 后序遍历

3.4 二叉树的递归遍历算法及分析
- 以上三种算法非常相似,只有输出根结点的位置不一样。
- 在先序遍历中将访问根结点的位置放在第一位,中序就放在中间,后序最后。
- 如果将以上三种算法中访问根节点的这段语句拿走,这三个算法是完全相同的。
- 或者说三中算法的访问路径是相同的,只是访问结点的时机不同而已。
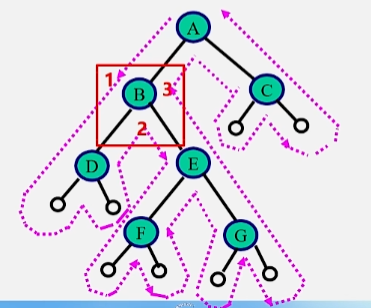
从上图看:
-
从虚线出发到终点的路径上,每个结点经过三次。
- 第一次经过时访问 = 先序遍历。
- 第二次经过时访问 = 中序遍历。
- 第三次经过时访问 = 后序遍历
-
第一次路过某个根结点的时候直接访问它,就相当于是先序遍历,如果将该结点的左子树访问完了之后,再回来访问该结点就是中序,后序同理。
时间复杂度
- 这三中算法的时间复杂度都是相同的,有 n 个结点的话就要遍历 n 个结点。
- 所以这三种算法的时间复杂度都为 O(n)。
空间复杂度
- 当遇到某个结点的时候,如果不访问它,就得找个空间将它记下来(这个结点没被访问),等回来的时候再来访问。
- 在最坏的情况下(单支二叉树),每个路过的结点都不访问都要存起来。
- 所以这三中算法最坏请况下的空间复杂度为 O(n)。
4. 遍历二叉树的非递归算法
中序遍历的非递归算法
二叉树中序遍历的非递归算法的关键:
- 在中序遍历过某结点的整个左子树后如何找到该结点的根以及右子树。
算法步骤
- 建立一个栈。
- 根结点进栈,遍历左子树。
- 根结点出栈,输出根结点,遍历右子树。
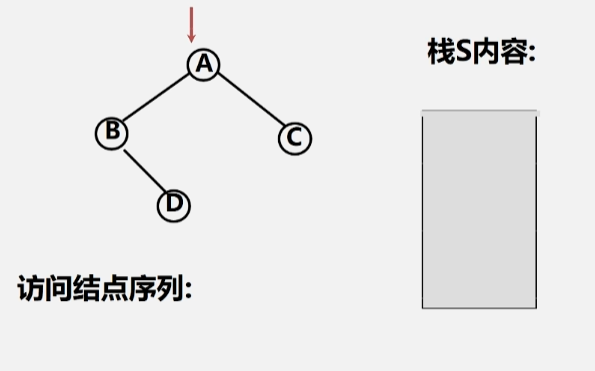
举个例子
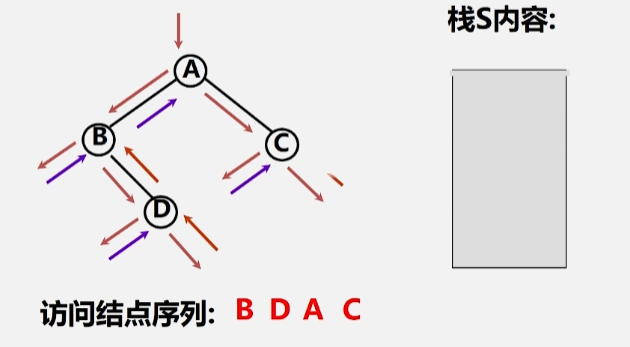
如下图所示的一棵二叉树的非递归遍历。
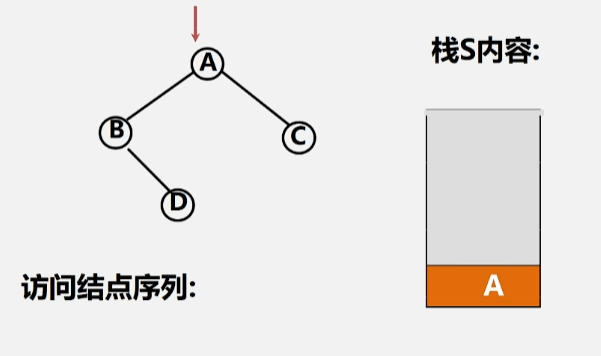
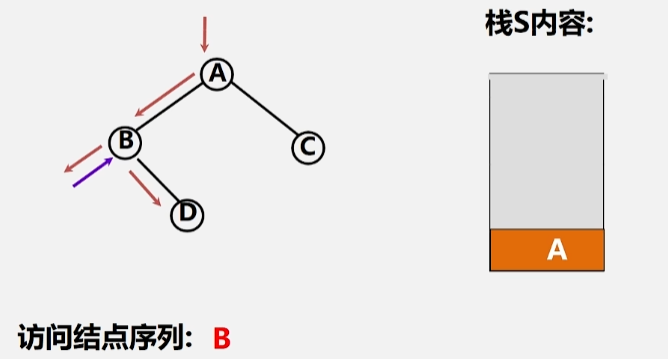
- 首先,遇到根节点 A 的时候不能访问它,必须先存到栈里头。
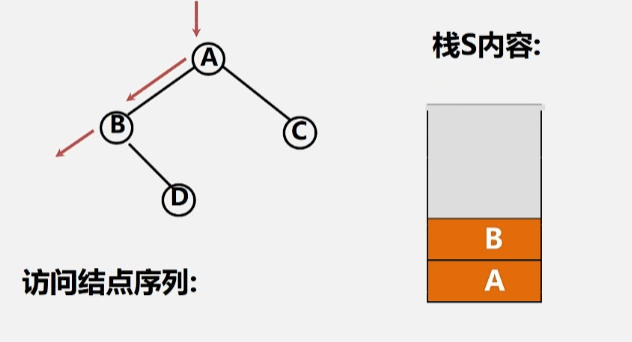
- 然后去访问 A 的左子树,同样的,B 结点为它所在的这棵树的根,先不能访问,得存进栈里。
- 将 B 存进栈里头了之后,再去访问 B 的左子树,发现左子树为空,这时候就该访问 B 结点了,所以将根结点 B 出栈。
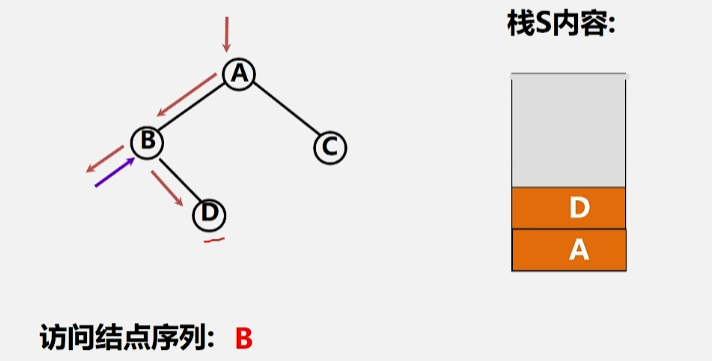
- 接下来就去访问 B 这个根结点的右子树 D 了。
- 到了右子树之后还是先遇到了根结点 D(存起来)。
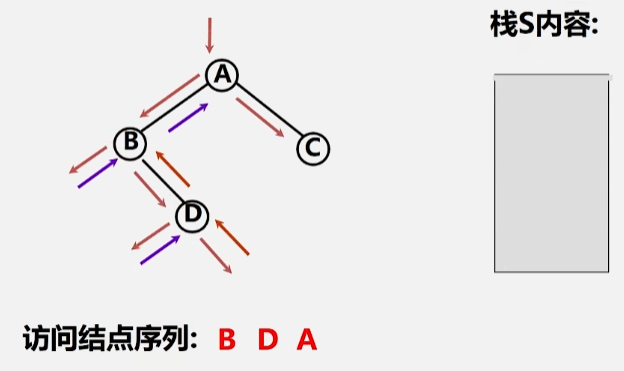
- 然后继续访问 D 的左子树,左子树为空,将 D 出栈,继续访问当前出栈元素(D)的右子树,右子树为空,此时 A 的左子树遍历完毕,将 A 出栈。
- 根结点访问完毕(出栈)之后,就该去访问该结点的右子树了。
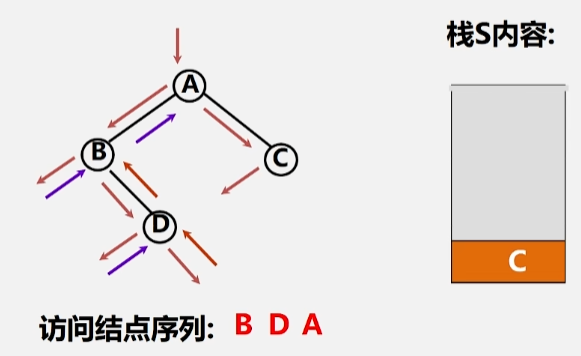
- 同样,遇到根(C)的时候不能访问,得先存起来,直到它的左子树为空的时候,就可以回头来访问(出栈)该结点了。
- 最后再访问刚出栈元素(C)的右子树,右子树为空的时候,回去看看栈里头还有没有元素,栈空的话则说明整趟遍历完成。
非递归遍历的算法描述
- 注:此算法仍然是在二叉链表上实现的。
//中序遍历二叉树 T 的非递归算法
Status InOrderTraverse(BiTree T)
{
BiTree p;//用指针 p 指向要操作的结点(出入栈)
InitStack(S);
p = T;//先将二叉树的根结点赋给 p
q = new BiTNode;
//申请一个结点空间 q 用来存放栈顶弹出的元素,
//q的定义在另一个函数
//当p指向的结点为空,并且栈也为空的时候,退出循环
while(p || !StackEmpty(s))
{
if(p)// p 指向的当前的根结点不为空
{
push(S,p);//将当前的根结点入栈
p = p -> lchild;
//去访问该根结点的左子树
}
else// p 当当前结点的左孩子为空时
{
Pop(S,p);//首先将栈顶元素弹出,
//这样做的目的是能够比较好的对当前遍历树的位置进行定位,
//以至于能做到对该节点右子树的后续遍历操作
cout << q -> data;//访问根结点
p = q -> rchild;//遍历右子树
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
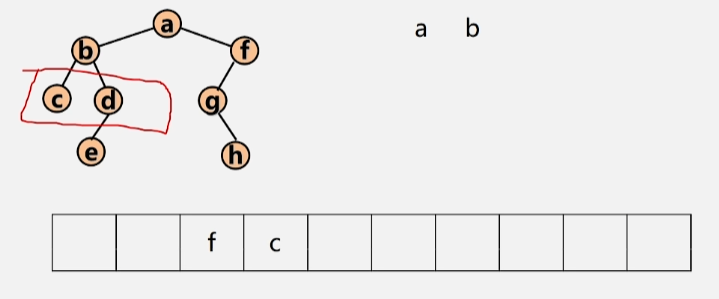
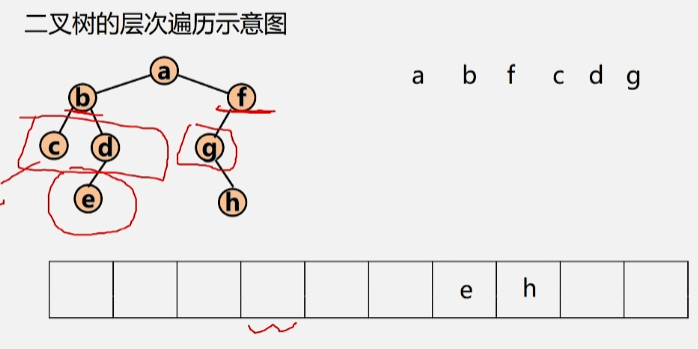
5. 二叉树的层次遍历算法
-
层次遍历:顾名思义就是按照二叉树的层数来遍历,第一层遍历完了之后遍历第二层,接着第三次以此类推。
-
对于一棵二叉树,从根结点开始,按照从上到下、从左到右的顺序访问每一个结点,且每个结点只访问一次。
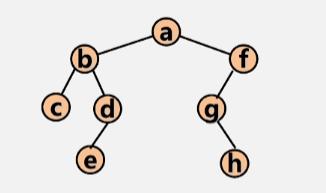
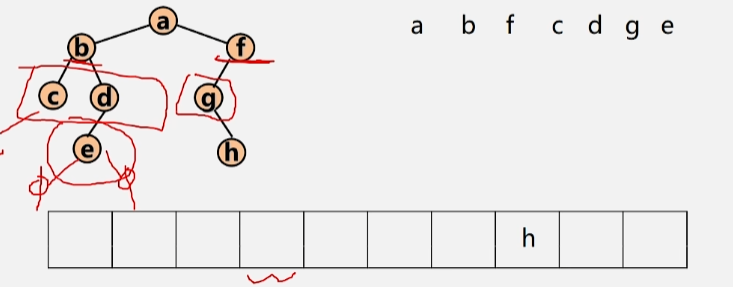
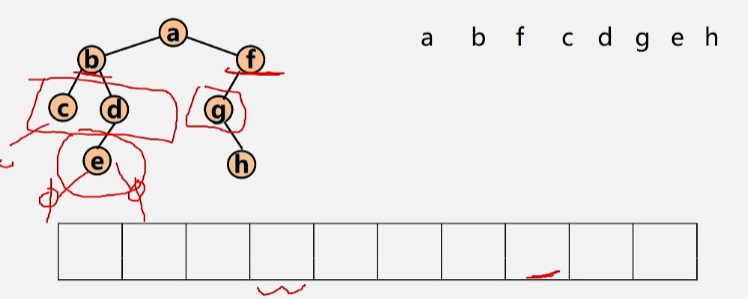
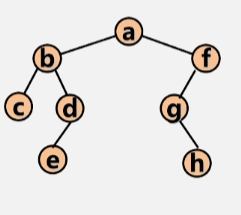
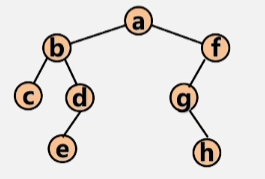
- 层次遍历结果:a b f c d g e h
算法思路:使用一个队列
- 将根结点进队;
- 队不为空时执行循环:不断从队伍中出队一个结点 *p,访问这个结点:
- 若它有左孩子结点,将左孩子结点进队;
- 若它有右孩子结点,将右孩子结点进队。
举个栗子
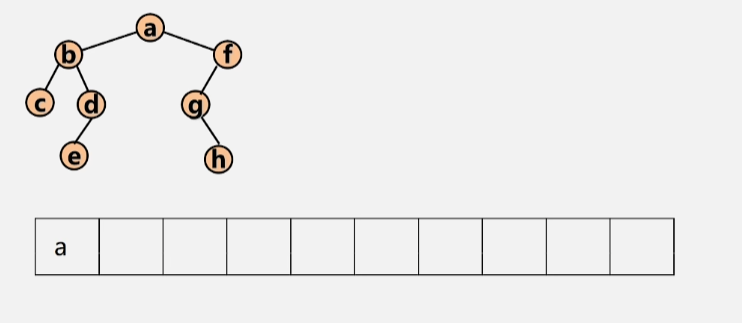
- 先将根结点 a 入队。
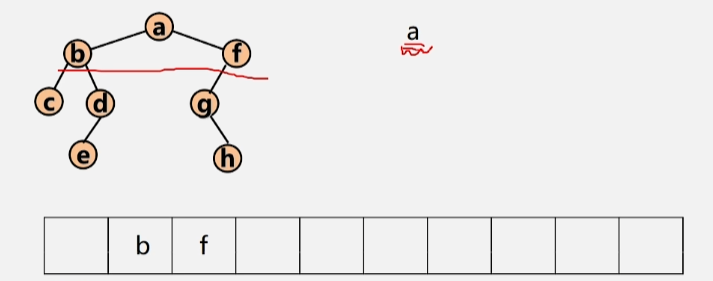
- 然后将当前队列当中的根结点 a 出队,在出队的同时,判断该结点时候有左右孩子,若有,则存进队中。
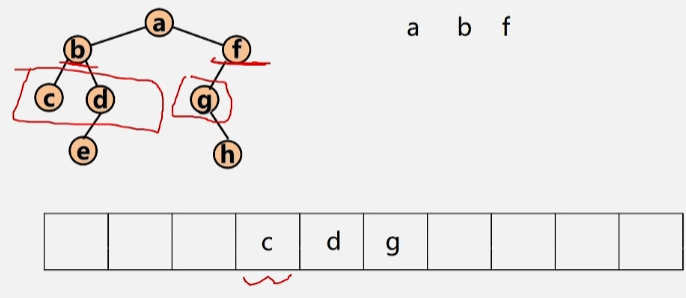
- 若队列当中还有元素,则继续出队,将 b 出队执行上述步骤,将 b 结点的左右孩子入队。
- 将 f 结点出队,将 f 的左孩子 g 入队。
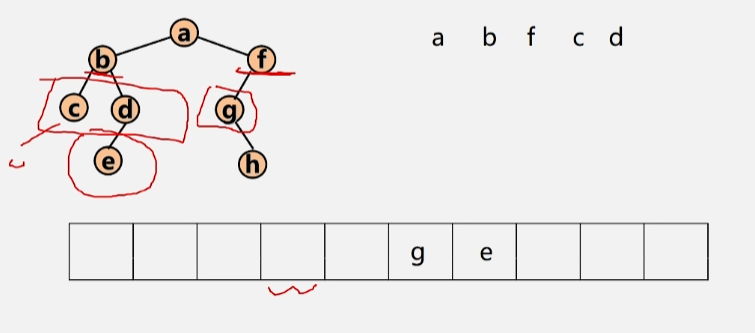
- 将 c 出队,c 无左右孩子,所以不管。d 出队,e 入队。g出队,h入队,然后依次出队,直到队空位置。
算法实现
- 这个队列依然用咱们用的最多的顺序循环队列。
//定义一个顺序循环队列
typedef struct
{
BTNode data[MAX];//存放队中元素
int front,rear;//队头和队尾指针
}SqQueue;//顺序循环队列类型
- 1
- 2
- 3
- 4
- 5
- 6
- 7
层次遍历算法
6. 二叉树遍历算法的应用
- 遍历是二叉树各种操作的基础,假设访问结点的具体操作不仅仅局限于输出结点数据域的值,而把访问延伸到对结点的判别、计数等其他操作,可以解决一些关于二叉树的其他实际问题。如果在遍历过程中生成结点,这样便可建立二叉树的存储结构。
6.1 先序遍历的顺序建立二叉链表
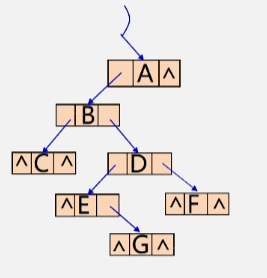
按照先序遍历序列建立二叉树的二叉链表。
例:已知先序序列为:A B C D E G F
- 从键盘中输入二叉树的结点信息,建立二叉树的存储结构。
- 在建立二叉树的过程中按照二叉树先序的方式建立。先建立根节点,然后建立左子树,最后建立右子树
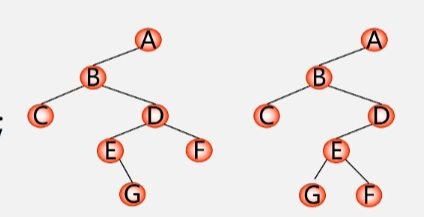
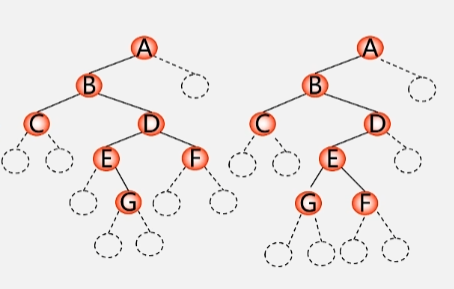
- 只知道先序序列的话,构造的树是不唯一的,下面两种树都有可能。
- 如果想建立的是第一棵树而不是第二棵,可以给这两棵树补充一些空节点,补充完之后这两棵树就不一样了。
- 空节点可以用空格符或者其他符号来表示
算法步骤
- 扫描字符序列,读入字符 ch
- 如果 ch 是一个 # 字符,则表示该二叉树为空树,即 T 为 NULL;否则执行以下操作:
- 申请一个结点空间 T。
- 将输入的字符 ch 符给结点的数据域 T->data。
- 递归创建 T 的左子树。
- 递归创建 T 的右子树。
算法描述
//按照先序次序输入二叉树中结点的值(一个字符),
//创建二叉树链表表示的二叉树 T
Status CreateBiTree(BiTree &T)
{
scanf(&ch);//将输入的值放到ch里
if('#' == ch);//如如果遇到了 # 字符就将当前的树构造为空树
{
T = NULL;
}
else//递归创建二叉树
{
T = (BiTNode*)malloc(sizeof(BiTNode));
//向内存中申请一块结点空间,并将该空间的首地址赋给T
if(!T)//如果开辟空间成功则执行以下操作
{
exit(OVERFLOW);//生成根结点
}
T -> data = ch;
//将根节点的数据域置为输入的字符 ch
CreateBiTree(T -> lchild);
//以当前结点的左孩子域为参数,递归构造左子树
CreateBiTree(T -> rchild);
//以当前结点的右孩子域为参数,递归构造右子树
}
return OK;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
6.2 复制二叉树
算法步骤
- 如果要复制的树为空树,则递归结束;
- 否则执行以下操作:
- 申请一个新结点空间,复制根结点。
- 递归复制左子树。
- 递归复制右子树。
算法描述
//复制一棵和 T 完全相同的二叉树
void Copy(BiTree T,BiTree &NEWT)
{
if(NULL == T)
{
//如果原来的树T是空树,递归结束
NewT = NULL;
return 0;
}
else
{
NewT = new BiTNode;
NewT -> data = T -> data;
//将根结点数据域的内容复制到新树的根结点
Copy(T -> lChile,NewT -> lchile);
//递归复制左子树
Copy(T -> rChile,NewT -> rchile);
//递归复制右子树
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
6.3 计算二叉树的深度
算法步骤
- 如果是空树,则递归结束,且返回深度为0,反之执行以下操作:
- 递归计算左子树的深度记为 m。
- 递归计算右子树的深度记为 n 。
- 如果 m 大于 n,二叉树的深度为 m + 1,反之为 n + 1,加的这个 1 是根结点的那一层。
算法描述
//计算二叉树 T 的深度(这棵二叉树有几层)
int Depth(BiTree T)
{
if(NUll == T)//如果是空树,则深度为0,递归结束
{
return 0;
}
else
{
m = Depth(T -> lchild);//递归计算左子树的深度记为 m
n = Depth(T -> rchile);//递归计算右子树的深度为 n
if(m > n)//返回二叉树的深度 m 与 n 的较大的那个值+1
{
return m + 1;
}
else//m小于或等于n的时候都可以返回n+1
{
return n + 1;
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
6.4 统计二叉树中结点的个数
- 如果是空树,则结点个数为 0。
- 反之结点个数为:左子树的结点个数 + 右子树的结点个数再 + 1(根节点)。
算法描述
- 先求左子树的左子树,再加上左子树的右子树,最后加上左子树的根。
//统计二叉树 T 中结点的个数
int NodeCount (BiTree T)
{
//如果是空树,则结点个数为 0 ,递归结束
if(NULL == T)
{
return 0;
}
//反之返回结点个数为左子树的结点个数+右子树的结点个树再+1
else
{
return NodeCount(T -> lchile) + NodeCount(T - rchild)+1;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
举个栗子
- 刚开始时指针是指向根节点 a 的,如果根节点不为空,则去统计它的左子树有多少个结点。
- 以 a 的左孩子结点 b 作为参数再次调用这个函数,
- 此时进入第三层调用,用当前根节点的左孩子 c 来调用这个函数。
- 再次以 c 为根节点调用它的左孩子,发现为空为 0,然后去算c的右子树,发现也为空(0),然后以c为根节点的这个左子树的结点数为 0 + 0 + 1 = 1。
6.5 计算二叉树中叶子结点数
- 可以模仿计算二叉树的深度这个算法,写出统计二叉树中叶子结点(度为0)的个数。
算法步骤
- 如果是空树,则叶子结点的个数为 0 。
- 否则,为左子树的结点个数 + 右子树的结点个数(不用加上根节点)。
算法描述
//统计二叉树㕜的叶子结点的个数
int LeafCount(BiTree T)
{
//如果T为空树,则叶子结点为0
if(NULl == T)
{
return 0;
}
//如果该结点的左右孩子都为空,则此结点为叶子结点,是叶子结点那就发现了一个叶子结点返回1
if(T -> lchild == NULL && T -> rchild == NULL)
{
return 1;
}
else
{
return LeafCount(T -> lchild)+LeafCount(T -> rchild);
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
举个栗子
- 如果T指向的当前的根节点不为空,则去看看该结点的左右孩子是否为空。
- 如果左右孩子都是空的,则返回1,表示只有一个叶子结点。
- 如果不是左右孩子都为空,则执行程序的 else 语句里的内容。
- 统计一下左子树的叶子,然后去统计右子树的叶子,最后加起来。
二、线索二叉树
为什么要研究线索二叉树?
- 当用二叉链表作为二叉树的存储结构时,可以很方便的找到某个结点的左右孩子;
- 但一般情况下,无法直接找到该结点在某种遍历序列中的前趋和后继结点。
提出的问题
- 如何寻找特定(先中后)遍历序列中二叉树结点的前趋和后继?
解决方法
- 通过遍历寻找 — 费时间。
- 给每个结点再增加两个指针域,用来存放该结点的前趋、后继结点 — 增加了存储负担。
- 利用二叉链表中的空指针域
1. 利用二叉链表中的空指针域
-
如果某个结点的左孩子为空,则将空的左孩子指针域改为指向其前趋。如果某结点的右孩子为空,则将空的右孩子指针域改为指向其后继。-
- 这种改变指向的指针称为线索。
- 加上了线索的二叉树称为线索二叉树(Threaded Binary Tree)。
-
对二叉树按某种遍历次序使其变位线索二叉树的过程叫做线索化。
举个栗子
- 有个以下图这棵二叉树为原型存储的二叉链表
- 根节点 A 没有右孩子,又因为 A 属于中序遍历的最后一个结点,它没有后继,所以继续空着。
- B 的左、右孩子指针域不为空,不管。
- C 结点没有左右孩子
- 又发现 C 是中序遍历的第一个结点,没有前趋结点,左孩子域继续为空。
- C 的后继结点是 B,将右孩子域改为指向 B 这个结点。
- D 结点没有空指针域,不管。
- E 没有左孩子,它的前趋是 B 结点,所以将左指针域内的指针改为指向 B 结点。
- F 没有左右孩子,将左指针指向 D 结点,右指针指向 A 结点。
- G 没有左右孩子,左指向 E,右指向 D。
为区分 lrchild 和 rchild 指针到底是指向孩子的指针,还是指针前趋或者后继的指针,对二叉链表中每个结点增加两个标志域 ltag 和 rtag其中:
- 若ltag = 0,则 lchild 指向该结点的左孩子。
- 若ltag = 1,则 lchild 指向该结点的前趋。
- 若rtag = 0,则 rchild 指向该结点的右孩子。
- 若rtag = 1,则 rchild 指向该结点的后继。
这样,结点结构就变成了:
二叉线索树结点类型定义
//二叉树的二叉线索存储表示
typedef struct BiThrNode
{
int data;//数据域,存储数据元素本身
int ltag,rtag;//左右标记域,存放 0 1
struct BiThrNode* lchild,rchild;//左右孩子指针
}BiThrNode,*BiThrTree;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
2. 构造线索二叉树
先序线索二叉树
- 存储线索的时候,存储的是它先序遍历下的前趋、后继。
- A 的两个指针分别指向左、右孩子,所以两个标记都是 0.
- B 没有左孩子,所以左孩子域存储 A 的地址,A 是 B 的前趋,所以 ltag为 1。右孩子指针指向的是 B 结点的右孩子 C 结点,所以 rtag为 0。
- C 结点左孩子指针指向前趋 B,ltag为1,右孩子域指向后继 D,所以 rtag 为 1。
- D 结点左孩子域指向 E,E为D的左孩子,所以 ltag为 0,D的右孩子域为空,所以指向D的后继E,rtag 为1.
- E 结点没有左右孩子,左孩子指向前趋D,ltag 为1,又因为E结点既没有右孩子也没用后继,所以右指针为空,且 rtag为1.
有了先序构造线索二叉树之后,中序、后序也是同样的道理。
中序线索二叉树
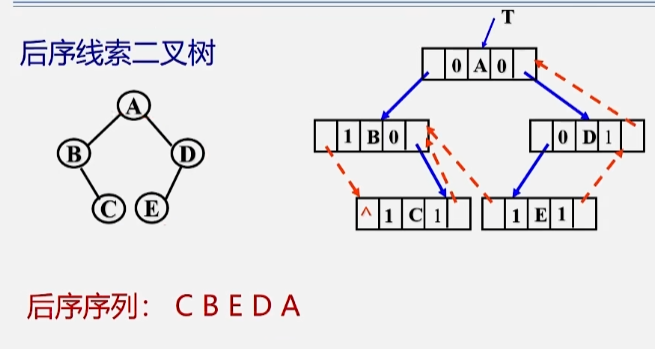
后序线索二叉树
小试牛刀
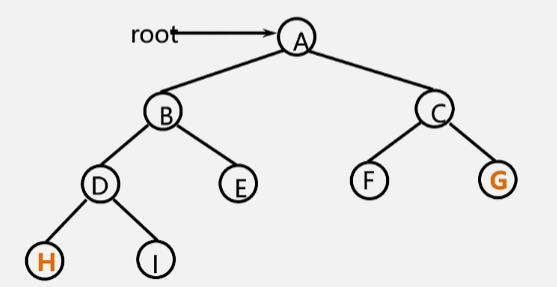
- 画出以下二叉树对应的中序线索二叉树。
- 该二叉树中序遍历结果为:H D I B E A F C G
- 先将叶子结点都利用起来,将他们所指向的前趋和后继先画出来
增加头结点
- 为了避免悬空状态,需要增设一个头结点,让悬空的指针指向头结点:
- ltag = 0,lchild 指向根结点;
- rtag = 1,rchild 指向遍历序列中的最后一个结点;
- 遍历序列中第一个结点的 lc 域和最后一个结点的 rc 域都指向头结点。