每周一刷——从斐波那契数列到动态规划

一、写在前面的话

在csdn上看到一篇博客，博客的内容有有关图像方面的paper，有有关机器学习的理论推导和python实践，文风简洁而不拖沓，非常喜欢，仿佛找到了同类，翻到“about me”以及一些求职的博文，方向选择之困惑，在求学期间学习方法之反思（实践、实践、还是实践）。仿佛看到了自己，看到了自己的明天，这位博主对算法之深刻，找工作之路尚感艰难，何况我呢。顿感企业要求之高（基础之看重），算法学习之路艰辛，学习之法之重要。这里，今天，特开一个算法系列，在基于数学的机器学习算法之外，重新整理更为基础的数据结构与算法。绳锯木断水滴石穿，星星之火可以燎原，为以后的求职之路打下基础。

既然是写在前面的话，不妨订立几条标准。

• 更新的频次上，$\geq$2篇/周；

• 不简单地粘贴代码，必须凝结自己的思考；

• 透过实现的技巧看算法的本质，通过代码理解基本概念；

• ……

这个系列主要参考的书有：

• 挑战程序设计竞赛

• 剑指ofter

二、普通版

首先以递归的形式定义Fibonacci数列的第$N$项$F(N)$的计算公式：

$$F(n) = \left\{ \begin{aligned} & n \qquad \qquad \qquad \qquad \quad n \leq 1\\ & F(n-1)+F(n-2) \quad n \geq 2 \end{aligned} \right.$$

根据此递归形式的定义，可得出二分递归版fib(n)算法：

// sizeof(__int64) == 8
// sizeof(__int64) == sizeof(long long)
// 注意斐波那契数列的增长速度是很快的，fib(40)的值已超过10^9
__int64 fib(unsigned n)     
{
    if (n <= 1)
        return n;
    else
        return fib(n-1) + fib(n-2);
}
1
2
3
4
5
6
7
8
9
10

简单的if-else语句又可进一步简化为三目运算符：

__int64 fib(unsigned n)
{
    return (n <= 1) ? __int64(n) : fib(n-1) + fib(n-2);
}
1
2
3
4

三、改进版

虽然定义、形式和实现上都十分简单和便于理解，二分递归版却存在大量重复计算的问题。以$F(10)$的递归计算为例考察二分递归版的重复计算问题，如图示：

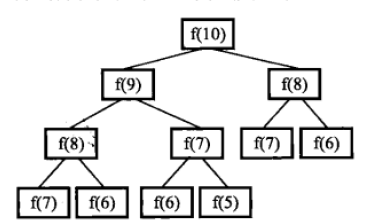
解决的思路便是考虑如何利用已计算的中间值来计算当前要计算的值，剑指offer给出的解决方案是，完全不在沿用传统的递归计算（从后向前的）方式，而是采用顺序的循环的向后计算方式，为了方便计算需引入两个中间变量

__int64 fibNMinus1, fibNMinus2;
1

分别表示$F(n-1)$、$F(n-2)$来记录每一次参与循环计算的第一个加数和第二个加数。代码如下：

__int64 fib(unsigned n)
{
    if (n <= 1)
        return n;
    __int64 fibNMinus1 = 1;
    __int64 fibNMinus2 = 0;
    __int64 fibN = 0;
    for (unsigned i = 2; i <= n; ++i)
    {
        fibN = fibNMinus1 + fibNMinus2；
        fibNMinus2 = fibNMinus1;
        fibNMinus1 = fibN;
    }
    return fbN;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

四、动态规划版

剑指offer提供的替代方案仍然具有一定的技巧性，所谓技巧性也即不可复制性，这里提供一种通用的解决方案，所谓的通用，是因为它利用了一种算法思想：动态规划（DP：dynamic programming），这里抛开动态规划严格且抽象的定义，我们从它的实现方式入手，也即记录结果再利用，我们来看动态规划版本的计算方法：

long long memo[N+1];        // 全局变量，初始化为0
long long fib(unsigned n)
{
    if (n <= 1)
        return n;
    if (memo[n]) return memo[n];
    else
        return memo[n] = fib(n-1) + fib(n-2);
}
1
2
3
4
5
6
7
8
9

这里看似好像仍然是之前的递归形式相同，然而，通过查看其递归调用的流程可以发现，分支的右侧，已在左侧计算出且保存在mem[n]中，

。

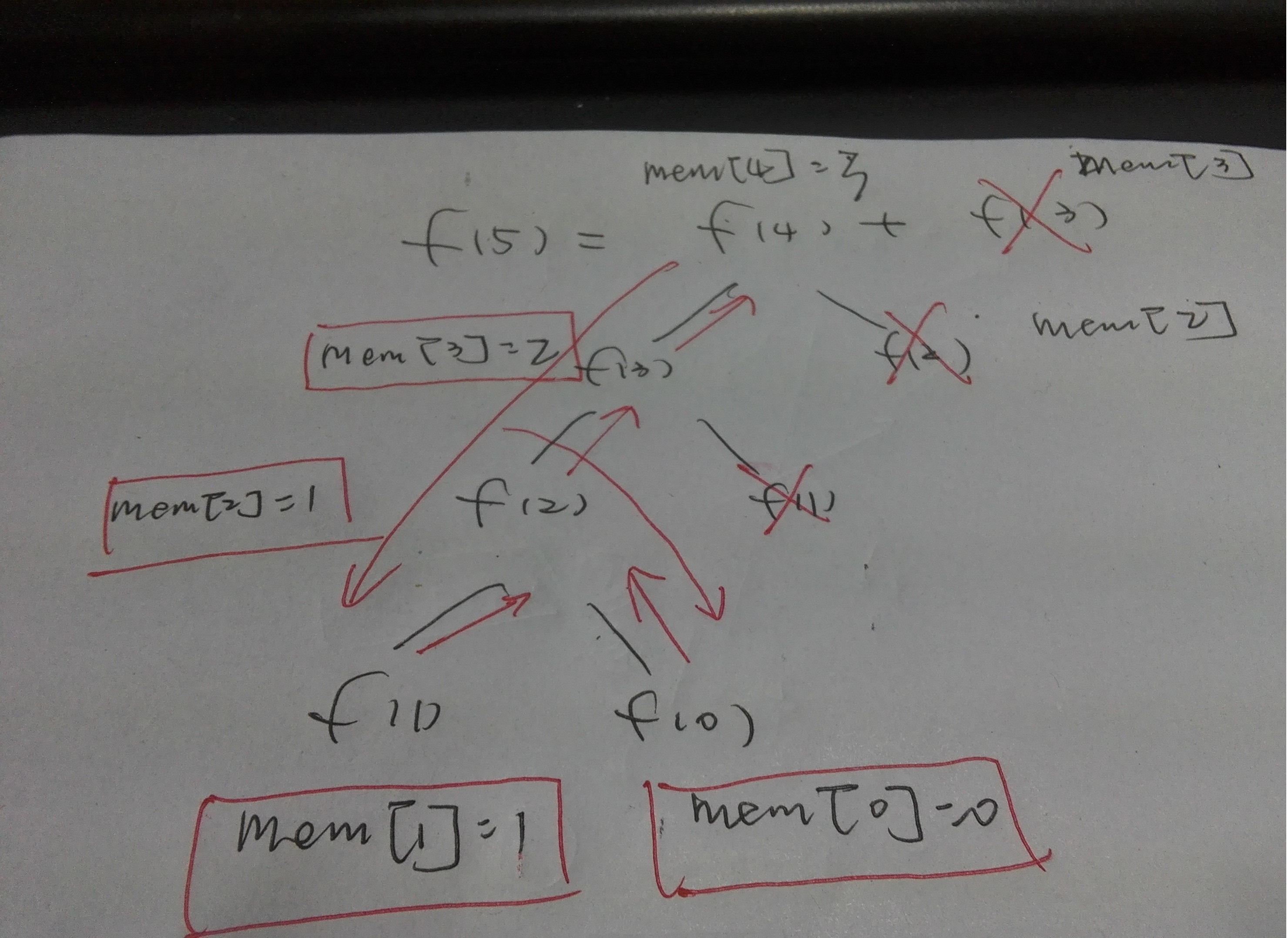
这篇博客的最终目的是为了引出动态规划的算法思想，自然想要把握动态规划的精髓，是完全不够的，会在以后的文章中反复思考和探索动态规划。