算法练习 DAY18 || 513.找树左下角的值 112.路径总和 113.路径综合ii 106.从中序与后序遍历序列 105.从前序与中序遍历序列构造二叉树

513.找树左下角的值

给定一个二叉树，在树的最后一行找到最左边的值。（在树的最后一行找到最左边的值）


要找出树的最后一行找到最左边的值。此时大家应该想起用层序遍历是非常简单的了，反而用递归的话会比较难一点。

递归（前序）

/* 递归 前序 */
/* 思路：用前序找到最大深度

递归三部曲：
1、形参就是当前前节点,以及这个节点的深度
2、终止条件：要找的是左叶子的值，所以遍历到叶子节点就return了。
3、单层逻辑：
本题设置全局变量 用来记录最大深度和result
*/
class Solution {
public:
	int maxdepth = -1;
	int result;

	void traversal(TreeNode* root,int depth) {
		if (root->left == nullptr&&root->right == nullptr) { //中
			//说明是一个叶子节点 此时就要去比较深度。
			if (depth > maxdepth) { //只有当depth>maxdepth的时候才会更新rsult
				//而因为中左右的顺序 同样深度的左叶子一定比右叶子先被找到
				//所以确保了找的值是 最左边的值
				maxdepth = depth;
				result = root->val;
			}
			return;
		}

		if (root->left) {  //左
			depth++;
			traversal(root->left, depth);
			depth--;  //这就是在回溯
			//traversal(root, depth + 1);  这种写法其实就隐藏着回溯的思想
		}

		if (root->right) { //右
			depth++;
			traversal(root->right, depth);
			depth--;
		}
	}
	int findBottomLeftValue(TreeNode* root) {
		//二叉树的节点个数的范围是[1, 104] 题目中给出如上信息
		//故无需判断头节点是否为空
		traversal(root, 1);
		return result;
	}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

迭代法（层序遍历）

//迭代法 层序遍历
class Solution1 {
public:
	int findBottomLeftValue(TreeNode* root) {
		queue<TreeNode*> que;
		int result = 0;
		que.push(root);
		while (!que.empty())
		{
			int size = que.size();
			for (int i = 0; i < size; i++) {
				TreeNode* temp = que.front();
				que.pop();
				//记录每一层第一个元素 也就是最左边元素
				if (i == 0) result = temp->val;
				if (temp->left) que.push(temp->left);
				if (temp->right) que.push(temp->right);
			}
		}
		return result;
	}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

112. 路径总和

给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。

说明: 叶子节点是指没有子节点的节点。

示例: 给定如下二叉树，以及目标和 sum = 22，
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。

class Solution {
public:
	/*
	递归
		1、返回值和形参：形参需要当前根节点和计数器
						 碰到符合条件的路线直接返回true就可以。
						 不需要遍历整棵树。所以返回值用bool类型
		2、终止条件：遍历到叶子节点
					 计数器值等于0了，返回true（让sun-root.val）
					 不一样就返回false
	*/
	bool traversal(TreeNode* node, int count) {

		if (node->left == nullptr && node->right == nullptr) {
			if (count == 0) return true;
			return false;
		}

		if (node->left) { //如果左孩子不为空
			
			//然后把这个左孩子当成中节点去处理 进入下一轮递归
			//那么count就减去node->left的值
			if (traversal(node->left, count - node->left->val)) return true;
			//上面这条语句隐藏了回溯的思想 展开来写以后就是
			/*count -= node->left->val;
			traversal(node->left, count);
			count += node->left->val;*/
		}

		if (node->right) {
			//traversal(node->right, count - node->right->val);
			//到某一个叶子节点返回true以后就不需要接着遍历了，让之前调用的traversal全都一层层返回true回去就可以了
			//所以写成如下形式
			if (traversal(node->right, count - node->right->val)) return true;
		}
		return false;
	}
	bool hasPathSum(TreeNode* root, int sum) {
		if (root == nullptr) return false;
		return traversal(root, sum - root->val);
	}
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

113.路径总合ii

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

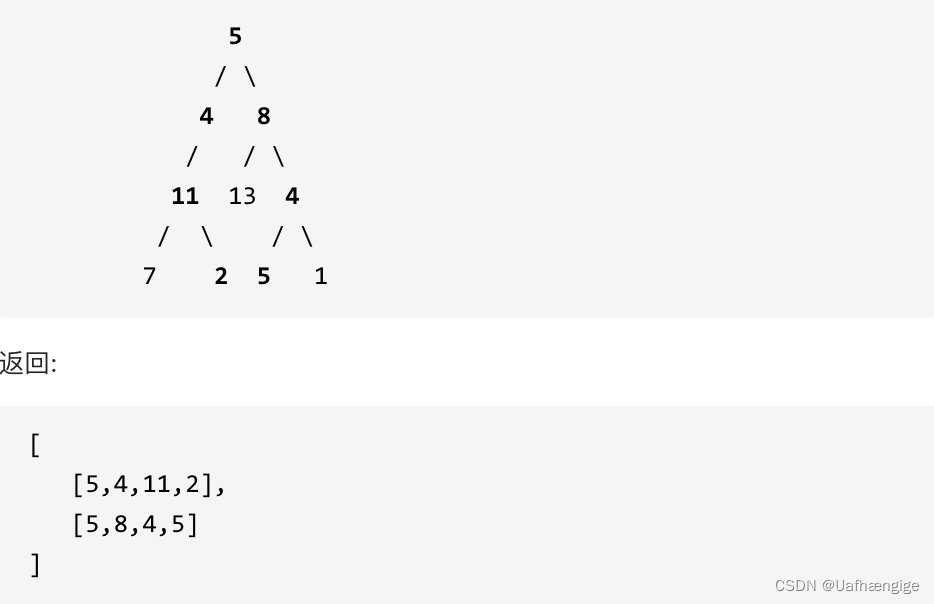
class Solution {
public:
	vector<vector<int>> result;
	vector<int> path;
	void traversal(TreeNode* cur, int count) {

		if (cur->left == nullptr&&cur->right == nullptr) {
			if(count == 0) result.push_back(path);
			return;
		}

		if (cur->left) {
			path.push_back(cur->left->val);
			traversal(cur->left, count - cur->left->val);
			path.pop_back();
		}

		if (cur->right) {
			path.push_back(cur->right->val);
			traversal(cur->right, count - cur->right->val);
			path.pop_back();
		}
		return;
	}
	vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
		if (root == nullptr) return result;
		//先把头节点的值加进来
		path.push_back(root->val);
		traversal(root, targetSum - root->val);
		return result;
	}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

106.从中序与后序遍历序列构造二叉树根据一棵树的中序遍历与后序遍历构造二叉树。

注意: 你可以假设树中没有重复的元素。

例如，给出

中序遍历 inorder = [9,3,15,20,7] 后序遍历 postorder = [9,15,7,20,3] 返回如下的二叉树：

class Solution {
public:
	TreeNode* traversal(vector<int>& inorder, vector<int>& postorder) {
		//如果后序数组为空 说明没有中节点
		if (postorder.empty()) return NULL;
		int rootValue = postorder[postorder.size() - 1];
		TreeNode* root = new TreeNode(rootValue);
		//如果后序数组只有一个元素，那说明遍历到叶子节点，直接返货该节点
		if (postorder.size() == 1) return root; 


		//根据后序数组的最后一个元素来切中序数组 找到左前序和右前序
		//注意保持同一种开闭区间！这里采用左闭右开
		
		//遍历中序数组
		int delimiterIndex;
		for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
			if (inorder[delimiterIndex] == rootValue) break;
		}

		//找到中节点所在的index，开始切割中序
		vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
		vector<int> rightInorder(inorder.begin() + delimiterIndex +1, inorder.end());

		//注意！中序与后序数组的大小一定是一样的！前序 左中右 后序 左右中
		//所以这个时候拿着leftinorder的大小去切后序数组，得到的一定是左后序
		// postorder 舍弃末尾元素
		postorder.resize(postorder.size() - 1);
		vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
		vector<int> rightPostorder(postorder.begin() + leftInorder.size() , postorder.end());

		root->left = traversal(leftInorder, leftPostorder);
		root->right = traversal(rightInorder, rightPostorder);

		return root;

	}
	TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
		if (inorder.size() == 0 || postorder.size() == 0) return NULL;
		return traversal(inorder, postorder);
	}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

105.从前序与中序遍历序列构造二叉树

class Solution {
private:
        TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& preorder, int preorderBegin, int preorderEnd) {
        if (preorderBegin == preorderEnd) return NULL;

        int rootValue = preorder[preorderBegin]; // 注意用preorderBegin 不要用0
        TreeNode* root = new TreeNode(rootValue);

        if (preorderEnd - preorderBegin == 1) return root;

        int delimiterIndex;
        for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
            if (inorder[delimiterIndex] == rootValue) break;
        }
        // 切割中序数组
        // 中序左区间，左闭右开[leftInorderBegin, leftInorderEnd)
        int leftInorderBegin = inorderBegin;
        int leftInorderEnd = delimiterIndex;
        // 中序右区间，左闭右开[rightInorderBegin, rightInorderEnd)
        int rightInorderBegin = delimiterIndex + 1;
        int rightInorderEnd = inorderEnd;

        // 切割前序数组
        // 前序左区间，左闭右开[leftPreorderBegin, leftPreorderEnd)
        int leftPreorderBegin =  preorderBegin + 1;
        int leftPreorderEnd = preorderBegin + 1 + delimiterIndex - inorderBegin; // 终止位置是起始位置加上中序左区间的大小size
        // 前序右区间, 左闭右开[rightPreorderBegin, rightPreorderEnd)
        int rightPreorderBegin = preorderBegin + 1 + (delimiterIndex - inorderBegin);
        int rightPreorderEnd = preorderEnd;

        root->left = traversal(inorder, leftInorderBegin, leftInorderEnd,  preorder, leftPreorderBegin, leftPreorderEnd);
        root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, preorder, rightPreorderBegin, rightPreorderEnd);

        return root;
    }

public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if (inorder.size() == 0 || preorder.size() == 0) return NULL;

        // 参数坚持左闭右开的原则
        return traversal(inorder, 0, inorder.size(), preorder, 0, preorder.size());
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45