DataMatrix 编码生成和译码原理即方法_ecc200编码规则

 

=====================================================

非常感谢博主 pooran

转载自：http://blog.sina.com.cn/s/articlelist_1165156174_0_1.html

===============================================================

DataMatrix编码的第一步骤，需要将原始信息转换成DataMatrix的码字，生成的码字范围（0,255）即unsigned char。通常的编码方式为Ascii编码，将原始字符+1即生成码字；同时为了压缩码长，若其中含有连续的两位数字，则将其+130后，生成一个unsigned char。如果要进一步压缩码长，还可以混合其他的编码方式：

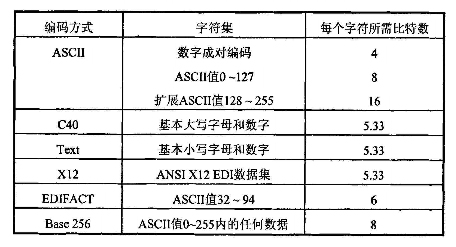
       当混入其他方式的编码时，需先插入一个切换字符，如由Ascii切换至C40，则插入230，再切换回Ascii时，则插入254。

       编码时，逐一对原始字符进行转换，如以下字符串：ABCDE12，转换后生成码字为：66 67 68 69 70 142。码长为6。

       根据码长，查下表规则，确定最终的码长：选择12*12的那一行，其码长为8。由于8-6=2，所以仍需插入2个码字，将其填满（避免生成的二维码出现大面积空白区域）。

ECC200的编码规则如下表：


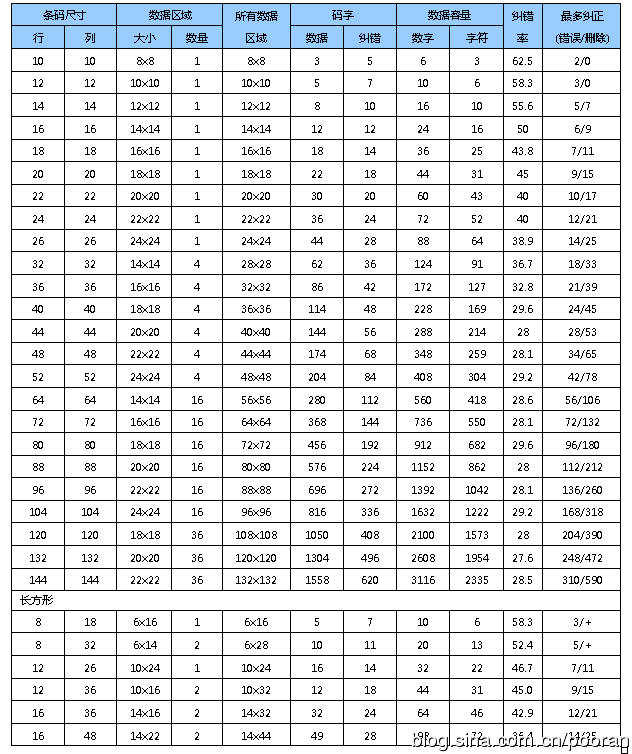
       计算此2码字：第一个码字为129（填充字符end of message），后面的各位为伪随机码，计算方法为253状态随机算法。公式： pseudorandom（n）  = (149 × n) mod 253 + 1，其中n为当前码字的位置（此时=8）， pseudorandom+129(mod 254)为最终码字 。故转换后最终码字为：66 67 68 69 70 142 129 56 。

----------------------------------------------------------------------------

伽罗华域即有限域，RS编码在此域中进行运算，故不得不对其有所了解。DataMatrix的数据码字、及纠正码字等均是属于GF(2^8)中的符号，其空间大小为256。有限域的一个特征是，其符号（元素）运算的结果，仍属于该域。除了0、1外，另外254个符号，均由本原多项式P(x)生成，DataMatrix规则中，P(x)=x^8+x^5+x^3+x^2+1，设α为P(x)的根，α^8+α^5+α^3+α^2+1=0，由于伽罗华域的加法为异或算法，故α^8=α^5+α^3+α^2+1。
       GF(2^8)符号的表示形式如下：
         计算机运算时，需要用相关算法将整个GF的所有符号的数值表示列表出来，结果如下：
alphaTo=
       {   1,     2,     4,     8,   16,   32,   64, 128,   45,   90, 180,   69, 138,   57, 114, 228,
         229, 231, 227, 235, 251, 219, 155,   27,   54, 108, 216, 157,   23,   46,   92, 184,
           93, 186,   89, 178,   73, 146,     9,   18,   36,   72, 144,   13,   26,   52, 104, 208,
         141,   55, 110, 220, 149,     7,   14,   28,   56, 112, 224, 237, 247, 195, 171, 123,
         246, 193, 175, 115, 230, 225, 239, 243, 203, 187,   91, 182,   65, 130,   41,   82,
         164, 101, 202, 185,   95, 190,   81, 162, 105, 210, 137,   63, 126, 252, 213, 135,
           35,   70, 140,   53, 106, 212, 133,   39,   78, 156,   21,   42,   84, 168, 125, 250,
         217, 159,   19,   38,   76, 152,   29,   58, 116, 232, 253, 215, 131,   43,   86, 172,
         117, 234, 249, 223, 147,   11,   22,   44,   88, 176,   77, 154,   25,   50, 100, 200,
         189,   87, 174, 113, 226, 233, 255, 211, 139,   59, 118, 236, 245, 199, 163, 107,
         214, 129,   47,   94, 188,   85, 170, 121, 242, 201, 191,   83, 166,   97, 194, 169,
         127, 254, 209, 143,   51, 102, 204, 181,   71, 142,   49,   98, 196, 165, 103, 206,
         177,   79, 158,   17,   34,   68, 136,   61, 122, 244, 197, 167,   99, 198, 161, 111,
         222, 145,   15,   30,   60, 120, 240, 205, 183,   67, 134,   33,   66, 132,   37,   74,
         148,     5,   10,   20,   40,   80, 160, 109, 218, 153,   31,   62, 124, 248, 221, 151,
             3,     6,   12,   24,   48,   96, 192, 173, 119, 238, 241, 207, 179,   75, 150,     0 }
同时，将各符号的指数也列表出来：
expOf=
     { 255,     0,     1, 240,     2, 225, 241,   53,     3,   38, 226, 133, 242,   43,   54, 210,
             4, 195,   39, 114, 227, 106, 134,   28, 243, 140,   44,   23,   55, 118, 211, 234,
             5, 219, 196,   96,   40, 222, 115, 103, 228,   78, 107, 125, 135,     8,   29, 162,
         244, 186, 141, 180,   45,   99,   24,   49,   56,   13, 119, 153, 212, 199, 235,   91,
             6,   76, 220, 217, 197,   11,   97, 184,   41,   36, 223, 253, 116, 138, 104, 193,
         229,   86,   79, 171, 108, 165, 126, 145, 136,   34,     9,   74,   30,   32, 163,   84,
         245, 173, 187, 204, 142,   81, 181, 190,   46,   88, 100, 159,   25, 231,   50, 207,
           57, 147,   14,   67, 120, 128, 154, 248, 213, 167, 200,   63, 236, 110,   92, 176,
             7, 161,   77, 124, 221, 102, 218,   95, 198,   90,   12, 152,   98,   48, 185, 179,
           42, 209,   37, 132, 224,   52, 254, 239, 117, 233, 139,   22, 105,   27, 194, 113,
         230, 206,   87, 158,   80, 189, 172, 203, 109, 175, 166,   62, 127, 247, 146,   66,
         137, 192,   35, 252,   10, 183,   75, 216,   31,   83,   33,   73, 164, 144,   85, 170,
         246,   65, 174,   61, 188, 202, 205, 157, 143, 169,   82,   72, 182, 215, 191, 251,
           47, 178,   89, 151, 101,   94, 160, 123,   26, 112, 232,   21,   51, 238, 208, 131,
           58,   69, 148,   18,   15,   16,   68,   17, 121, 149, 129,   19, 155,   59, 249,   70,
         214, 250, 168,   71, 201, 156,   64,   60, 237, 130, 111,   20,   93, 122, 177, 150 }
符号的运算：
a+b：=a^b，例如66+67=66^67=1
a*b：1、两指数相加，2、Mod（255）,3、求新指数对应的符号，例如66*67，指数分别为expOf(66)=220、expOf(67)=217，新指数为182，对应符号alphaTo(182)=204，即66*67=204。

         GF(2^8)空间的生成算法如下：

int MM = 8;
int NN = 255;
int alphaToMM = 45;//α^8=α^5+α^3+α^2+1
int* alphaTo = new int[NN+1];
int* expOf = new int[NN+1];

alphaTo[MM] = alphaToMM;
expOf[alphaToMM] = MM;
alphaTo[NN] = 0;
expOf[0] = NN;

int i, shift;
shift = 1;
for(i=0; i<MM; i++){
       alphaTo[i] = shift;//2^i
       expOf[alphaTo[i]] = i;
       shift <<= 1;
}
shift = 128;
for(i=MM+1; i<NN; i++){
       if(alphaTo[i-1] >= shift){
              alphaTo[i] = alphaTo[MM] ^ ((alphaTo[i-1]^shift)<<1);//alphaTo[i-1]*alpha+alpha^8
       }else{
              alphaTo[i] = alphaTo[i-1]<<1;
       }
       expOf[alphaTo[i]] = i;
}

-----------------------------------------------------------------------------------

 DataMatrix ECC200采用Reed-Solomon纠错编码来为其提供纠错能力。RS编码的目标是计算出纠错码字，参考表来确定纠错码字的长度，考虑数据码字：66 67 68 69 70 142 129 56（“ABCDE12”通过ASCII编码），长度为8，则纠错码字长度为10，表示为RS(n,k)=RS(18, 8)。
       设C(x)为数据码 ，
   E(x)为纠错码字 ，G(x)为生成多项式，则：
       
       由RS检验码生成多项式的一般形式为： ，则有：     
X分别取值 ，得到方程组：
     
     然后用通过高斯消除法计算出E(x)={75 145 55 46 20 95 253 237 62 111}，最终生成18位码字{66 67 68 69 70 142 129 56 75 145 55 46 20 95 253 237 62 111}。

算法如下：
int GfAdd(int a, int b){
  return  a ^ b;
}
//a * b
int GfMult(int a, int b){
   return (a == 0 || b == 0) ? 0 : alphaTo[(expOf[a] + expOf[b]) % nn];
}
// a * alpha^b
int GfMult2(int a, int b){
   return a== 0 ? 0 : alphaTo[(expOf[a] + b) % nn];
}
// a/b
int GfDiv(int a, int b) {
    if( a==0 )return 0;
    if( a==b )return 1;
    return expOf[a] > expOf[b] ?
    alphaTo[ expOf[a] - expOf[b] ] : alphaTo[ nn + expOf[a] - expOf[b] ] ;
}
void gaussion(){
    int total = 18;
    int data = 8;
    int error = 10;
    int* codes = new int[total];
    int* errors = new int[error];
    int* polys = new int[error*error];

    int i, j, k, d;       
    codes[0] = 66;
    codes[1] = 67;
    codes[2] = 68;
    codes[3] = 69;
    codes[4] = 70;
    codes[5] = 142;
    codes[6] = 129;
    codes[7] = 56;

    for( i=0;i<error;i++ ){
        //sum of each polynomial
        int sum = 0;
        for( j=0;j<data;j++ )
            sum = GfAdd( sum, GfMult2( codes[j], (total-1-j)*(i+1) ) );
        errors[i] = sum;
        //polynomial matrix
        int index = i*error;
        for( j=0;j<error;j++ )
            polys[index+j] = alphaTo[j*(i+1)];
    }
    //gaussion elimination
    for( i=0;i<error;i++ ){
        //diagonal postion
        d = i*error+i;
        int diagonal = polys[d];
        //diagonal --> 1
        int index = i*error;
        for( j=0;j<error;j++ )
            polys[index+j] = GfDiv( polys[index+j], diagonal );
        errors[i] = GfDiv( errors[i], diagonal );
        //otherrows - thisrow
        for( k=0;k<error;k++ ){
            if( k!=i ){//another row
                int index2 = k*error;
                int coefficient = polys[index2+i];
                //each column( polynomial[k] = polynomial[k] - polynomial[i]*coefficient )
                for( int m=0;m<error;m++ ){
                    polys[index2+m] = GfAdd( polys[index2+m], GfMult(coefficient, polys[index+m]) );
                }
                errors[k] =GfAdd( errors[k], GfMult(coefficient, errors[i]) );
            }
        }
    }
    //errors --> codes
    for( j=data++,i=error-1;i>=0;i-- )
        codes[j++] = errors[i];
}

======================================================================================

以下为译码算法

======================================================================================

 设“ABCDE12”通过RS编码后为C(x)={66 67 68 69 70 142 129 56 75 145 55 46 20 95 253 237 62 111}，经过信道时发生了失真，接收到的数据为R(x)={66  99 68 69 70 142 129 56 75 145 55 46 20 95 253 237 62 111}。译码的首先需要通过纠错将T(x)还原出来。
       设有RS(n,k)，其中包含数据码字k个，冗余码字n-k个，可纠正错误t=(n-k)/2个；在本例中，n=18，k=8，冗余10个，可纠错5位。纠错过程如下：
     
1、生成伴随式{S 1, S 2, ……, S 2t}
     设接收码字 ，
     先计算出伴随式 ， i = 1,2,……2t；显然，若接收码字R(x)无任何错误，则S i = 0；反过来，若S i全部=0（i = 1,2,……2t），说明接收码字无错误，即R(x) = C(x)。   
     设E(x)为错误图样 ，
     若信道产生了t个错误，则E(x)也可以表示为：
    ，其中每一个 ，表示各个错误位置，Y i为该位置上的错误值。
     由于 R(x) = C(x)+E(x)，
  ，i = 1,2,……2t；又由于 ，所以
  ,   即 ，得到方程组①：
        

2、求错误位置多项式 σ(x)
       目前已知Si，要通过方程组①求得X 1~ X t，需要借助下面的“错误位置多项式”：
  , 其中Xi来自E(x)，现在借助方程组①，建立{ σ1, σ2……, σt}与{S1,S2 ……,St}之间的关系。
    σ (x)=0的根为 ，故而可以构建以下方程组：
  
   现在开始变换：
   第1步：上述1 ~ t个等式，第i个等式左右分别乘以 ，得：
  
     将 σi的系数相加，结合 方程组①，可以得到：
  
  第2步：上述1 ~ t个等式，第i个等式左右分别乘以 ，同理得：
   
  第t步：上述1 ~ t个等式，第i个等式左右分别乘以 ，同理得：
   
   如此得到方程组，得到Si与 σi之间的关系（ Xi与Yi已经消失了）：
  
   通过解方程组，求出 { σ1, σ2 ……, σt} 。

3、求出错误位置Xi
  由于 ， σ (x)=0的根为 ，将 逐一取倒数代入 σ (x)，若 ，则i即为错误位置。

4、求错误值Yi
   求出Xi后，设得到r个实际有错误的位置（r<=t），分别为 ，需要求出其对应的正确码字 ；其余n-r位码字均为正确码字，由 建立以下方程组：
  
   解方程即可求出 ，将其按 逐一把R(x)替换掉即可将C(x)还原出来。

---------------------------------------------------------------------------------------

 经过纠错后，我们得到正确的码字C(x)={66 67 68 69 70 142 129 56 75 145 55 46 20 95 253 237 62 111}，该组码字为“ABCDE12”通过ASCII+RS编码得来，现在的任务是从改组码字把原始信息还原出来，即求出“ABCDE12”。
       C(x)的长度为18，其中数据码字为前8位，用于纠错的冗余码字为后10位，现在冗余码字已经无用了，只需用到数据码字：设C(x)={66 67 68 69 70 142 129 56 75}，考虑C(x)是怎么由原始信息“ABCDE12”转换而来的，其逆过程即可将原始信息还原。
       再次参考ASCII编码规则：
  
       逆过程如下：
1、指针ptr指向第一个码字，若其=236或237（05或06Macro），则表示采用了Macro标准，先输出Macro头：[)>' 30'0 5或6' 29'，ptr+1；否则指针不变；
2、逐一对*ptr进行判断，若=切换字符：230、231、232...等，则切换到相应的编码方式，同时ptr+1；否则即为默认的编码方式：Ascii，且ptr不变；
3、若采用了Macro标准，则输出Macro尾：' 30'' 4'


参考： http://en.wikipedia.org/wiki/Data_Matrix

举例Base256 mode编码:
1、输出切换字符231
2、输出待编码的数据的长度N：
     若N<250，则对N进行255伪随即状态算法，后输出
     若N>=250，则需将N分为两个byte，N1=N/250+249(250~255)，N2=N%0(0~249)，将N1、N2分别进行255算法后输出
3、分别对各位待编码的数据进行255算法后输出
255算法： x+=R(n)，R(n) = (149 × n) mod 255 + 1，——n为第?个数据，如N1时n=2（切换字符231为第1个）