Atcoder 287 题解（A-D）_a - tcdr atcoder

A - Majority

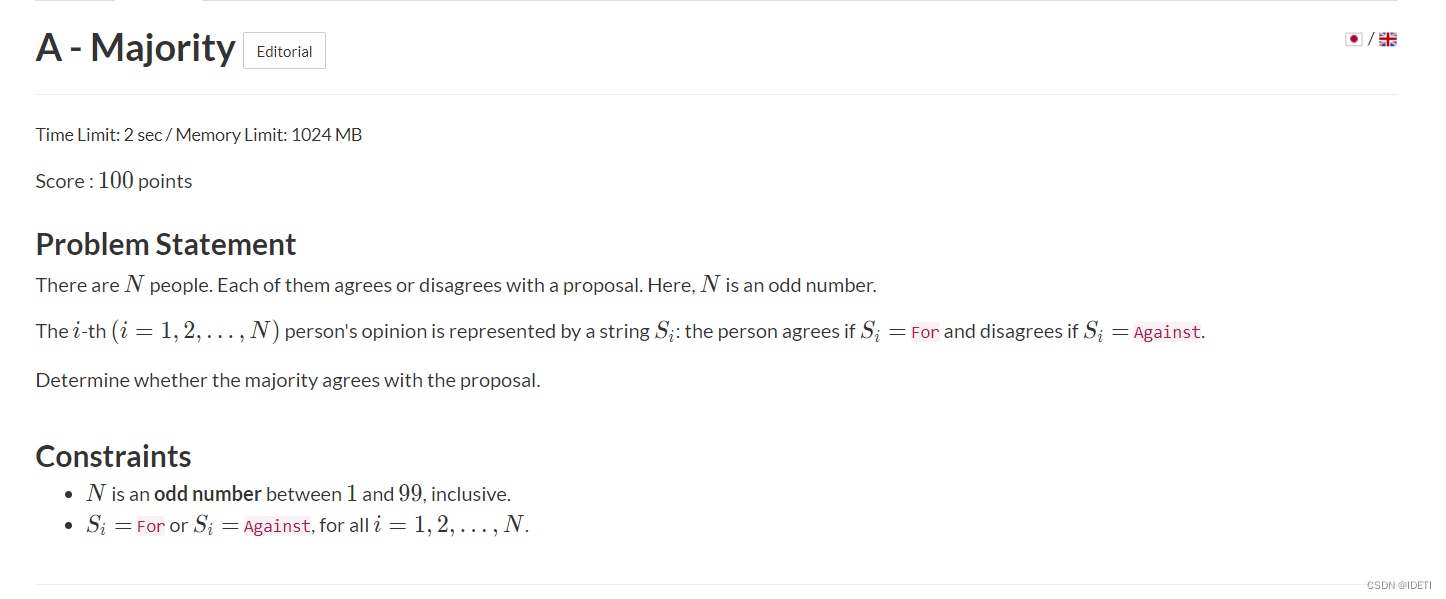题意：现在有N个人和一个建议，每个人给我们一个字符串，每个字符串都是For（赞同）或者Against（反对），让我们求出最后大多数人们是反对还是赞同我们的建议。

简单题直接枚举一下赞同和反对的总数，最后进行比较一下就行

代码：

#include <bits/stdc++.h>
 
using namespace std;
int n;
int a, b;
int main()
{
    cin >> n;
    while (n--)
    {
        string str;
        cin >> str;
        if (str == "For")
            a++;
        if (str == "Against")
            b++;
    }
    if (a > b)
        puts("Yes");
    else
        puts("No");
    return 0;
}

B - Postal Card 

题意：

给我们一个n和m,接着给我们n个字符串长度为6的字符串(只包含数字)Si(1<i<n),接下来还会给我们m个长度为3的字符串(只包含数字)Ti(1<i<m)，他让我们区数一下有多少个Si的后三个数字和Ti的数一一对应，并输出这个个数

我一看string就直接用string写了，实际上我们可以使用int类型去存储那个数，直接去做就行

代码：

#include <bits/stdc++.h>
 
using namespace std;
const int N = 1010;
int n, m;
int s[N];
map<int,int> t;
map<string, int> mp;
void solve1()//使用字符串去做，稍微有点麻烦
{
    cin >> n >> m;
    string s[N], p[N];
 
    for (int i = 0; i < n; i++)
        cin >> s[i];
    for (int i = 0; i < m; i++)
    {
        cin >> p[i];
        mp[p[i]]++;//将后三个数字存储一下，一会和s字符串相匹配
    }
    int res = 0;
    for (int i = 0; i < n; i++)
    {
        string str;
        str = s[i].substr(3, 6);//取出si字符串的后三位
        if (mp[str] >= 1)
            res++;
    }
    cout << res << endl;
}
void solve2()
{
    cin >> n >> m;
    for (int i = 0; i < n; i++)
        cin >> s[i];
    for (int j = 0, x; j < m; j++)//同上
    {
        cin >> x;
        t[x]++;
    }
    int res = 0;
    for (int i = 0; i < n; i++)
        if (t[s[i] % 1000] >= 1)//如果这个后三位在t数组中出现过，答案++
            res++;
    cout << res << endl;
}
int main()
{
    solve();
    return 0;
}

C - Path Graph? 

 题意：

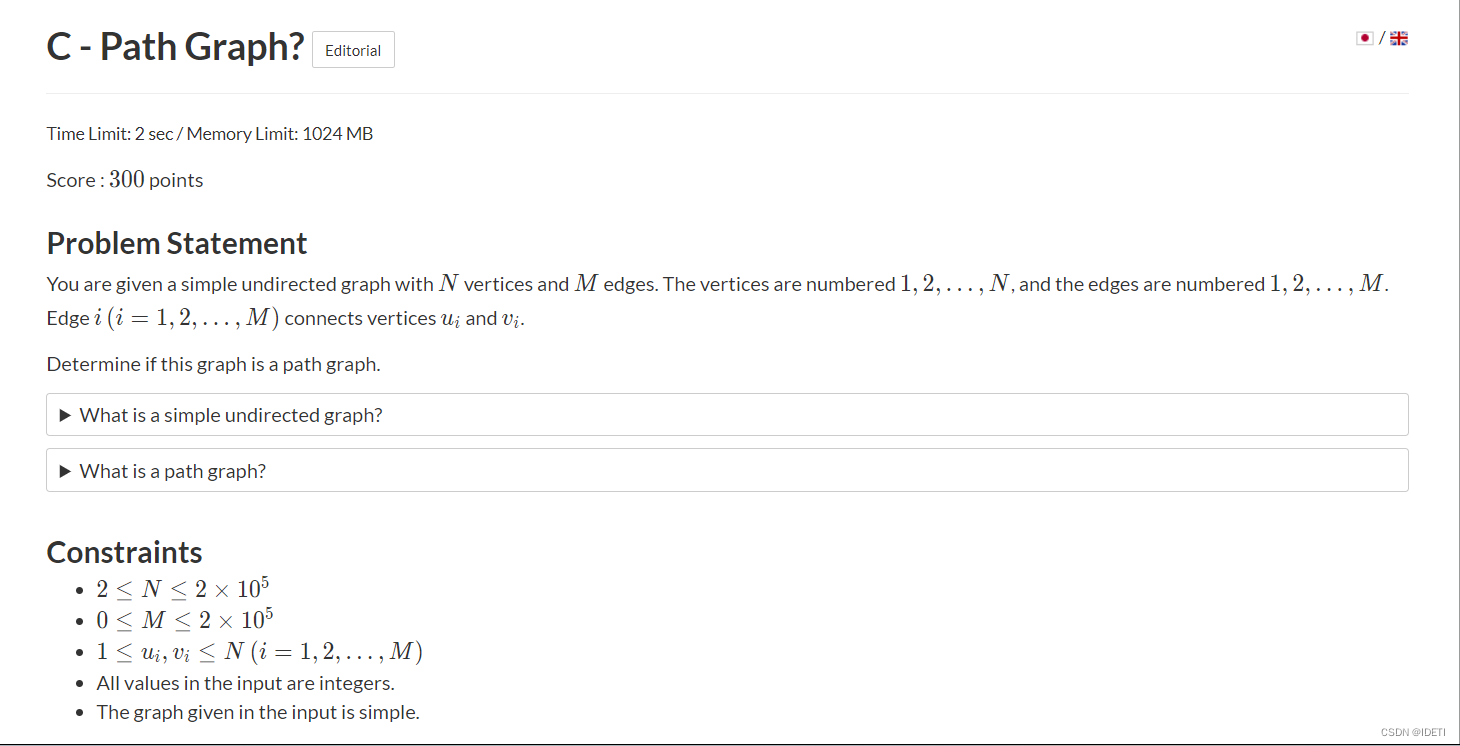
给我们一个无向图，有n个顶点，m条边，让我们判断一下当前的这个无向图是否为路径图

路径图：

1.M=N-1（大家可以想一下为什么）

2.连通图（所有的点都是连同的）

3.每个点的度数小于等于2（换句话来说就是每个点至多和两个点相连接）

第一个条件很好实现，第二个稍微麻烦一点，我们可以使用dfs或者bfs遍历一遍整个图，然后去找一下是否有点没有出现在我们的连通图中，如果有的话就说明我们的图连通的部分大于1个，或者使用并查集的算法去解决这个问题，不过这个好像在这次比赛结束后给卡了一下（我也不清楚为啥）最后一个我们可以使用vector存储图，最后遍历一下每个点就可以啦

代码如下(第一个是正确的，第二个不知道为啥后面又被hack了）

#include <bits/stdc++.h>
 
using namespace std;
 
const int N = 2e5 + 10;
int n, m;
void solve()
{
    vector<vector<int>> map(n + 1);
    for (int i = 0; i < m; i++)
    {
        int a, b;
        cin >> a >> b;
        map[a].push_back(b);
        map[b].push_back(a);
    }
 
    if (m != n - 1)
    {
        cout << "No" << endl;
        return;
    }
    for (int i = 1; i <= n; i++) //每个点的度数都得小于等于2
        if (map[i].size() > 2)
        {
            cout << "No" << endl;
            return;
        }
 
    // dfs遍历图
    vector<bool> s(n + 1); //遍历连通图，看一下是否存在不在一个连通图的点
    //即判断当前的图的连通度是否为1
    queue<int> q;
    s[1] = true;
    q.push(1);
    while (!q.empty())
    {
        int x = q.front();
        q.pop();
        for (int v : map[x])
        {
            if (!s[v])
            {
                s[v] = true;
                q.push(v);
            }
        }
    }
 
    for (int i = 1; i <= n; i++)
    {
        if (!s[i])
        {
            cout << "No" << endl;
            return;
        }
    }
    cout << "Yes" << endl;
}
int main()
{
    cin >> n >> m;
    solve();
    return 0;
}

第二份代码：（现在已经叫不上了）

#include <bits/stdc++.h>
 
using namespace std;
const int N = 2e5 + 10;
int n, m;
int p[N];
int find(int x) //并查集算法！！
{
    if (x != p[x])
        p[x] = find(p[x]);
    return p[x];
}
void solve()
{
    cin >> n >> m;
    for (int i = 1; i < n; i++)
        p[i] = i;
 
    int cnt = n, flag = 0;
    for (int i = 0; i < m; i++)
    {
        int a, b;
        cin >> a >> b;
        a = find(a);
        b = find(b);
        if (a != b)
        {
            p[a] = b;
            cnt--;
        }
        if (a == b)//自环的情况
            flag = 1;
    }
 
    if (flag || cnt != 1)
        cout << "No" << endl;
    else
        cout << "Yes" << endl;
}
int main()
{
    solve();
 
    return 0;
}

希望这篇题解对您的学习有帮助，有任何问题都可以私信我