weixin_40725706

这个屌丝很懒，什么也没留下！

热门标签

热门文章

当前位置: article > 正文

线性代数--矩阵计算（加减乘法）_矩阵运算

作者：weixin_40725706 | 2024-06-29 19:54:34

赞

踩

矩阵运算

目录

一、矩阵的基本概念

1、行矩阵与列矩阵

1）、方阵的定义

2）主对角线和次对角线

6、只有一个数字的矩阵

7、同型矩阵

二、矩阵与行列式的区别

三、矩阵的运算

1、加法、减法

2、数乘运算

四、矩阵乘法

1、矩阵的乘法

2、矩阵乘法不满足的三条规律

3、矩阵乘法的运算规律

4、矩阵的可交换

五、矩阵的幂运算

六、简单的矩阵运算，学到的知识点运用起来。

一、矩阵的基本概念

矩阵本质上是一个数表，用 $_{}$ $A_{m*n}$ 表示，代表一个m*n的矩阵，有m行n列。

矩阵的运用场景非常多，例如关系的表示等。

如下图就是一个4行4列的矩阵。

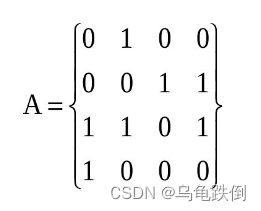
1、行矩阵与列矩阵

只有1行的矩阵叫做行矩阵

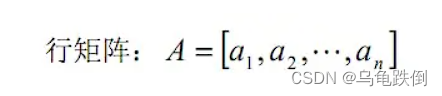
只有1列的矩阵叫做列矩阵

2、零矩阵

矩阵内的所有元素都是0，记作O

3、负矩阵

把原来矩阵的所有元素都取负号，为相反数，称为负矩阵。

例如 $A$ 的负矩阵为 $-A$ 。

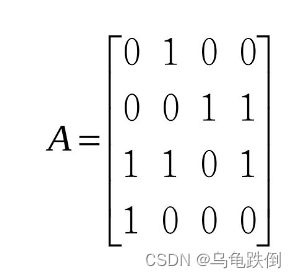
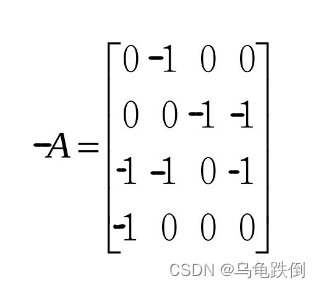
4、方阵

1）、方阵的定义

行数等于列数的矩阵称为方阵，一般也称为n阶矩阵，即 $A_{n*n}$ ，亦 $A_{n}$

例如下面这个矩阵，就是三行三列的矩阵。

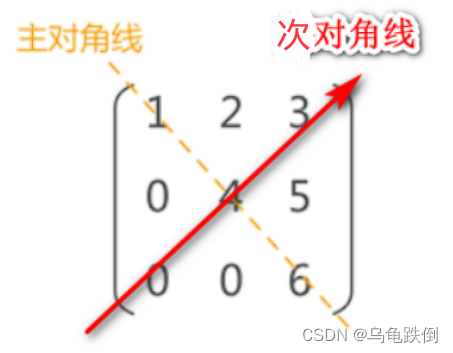
2）主对角线和次对角线

只有在方阵中才有对角线的概念。如图：

5、单位阵

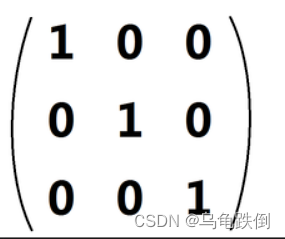
对角线为1，其余元素为0，这种矩阵称为单位矩阵。记作E。

6、只有一个数字的矩阵

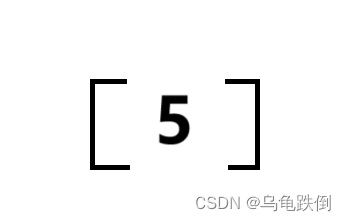
只有一个数字的矩阵也是矩阵，可视作特殊的矩阵。

例如：[5]

7、同型矩阵

两个矩阵形状一样，称为同型矩阵。即行数和列数相等。

例如： $A_{2*3}$ 和 $B_{2*3}$ 就是同型矩阵。

如果同型矩阵的对应元素相等，那么两个矩阵相等。即相等矩阵的前提是同型矩阵。

二、矩阵与行列式的区别

1、本质上，矩阵是一个数表，而行列式是一个数。

2、符号：矩阵使用 $\left ( \right )$ 或者 [ ]，而行列式使用 $\left | \right |$

3、形状上，矩阵不一定是方阵，但是行列式一定是一个方阵，即行数等于列数。

三、矩阵的运算

1、加法、减法

对应元素相加减。（注意：只有同型矩阵才能相加减）

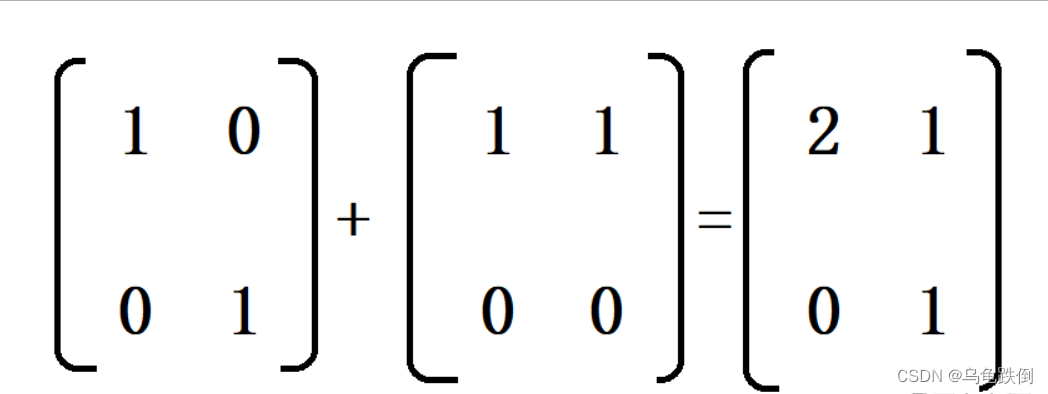
矩阵加减法满足的运算法则也很简单:

A+B=B+A

(A+B+C) = A+(B+C)

A+(-A)=0

A+B = C $\Leftrightarrow$ A = C - B

2、数乘运算

k乘以矩阵的所有元素。

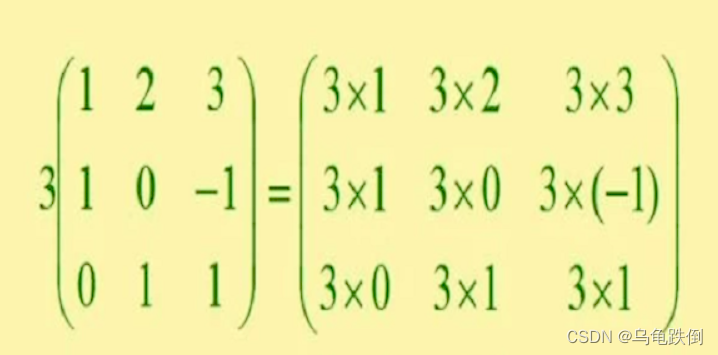
矩阵数乘和行列式的区别

矩阵提公因子：矩阵所有元素均有公因子，公因子朝外提一次

行列式提公因子：一行（或者一列）提取一次，如果所有元素都有公因子，有n行则提n次。

矩阵数乘满足的运算规律：

k(A+B) = kA + kB

(k+m)A = kA + mA

k(mA) = kmA

四、矩阵乘法

1、矩阵的乘法

第一行乘以第一列，先相乘后相加。

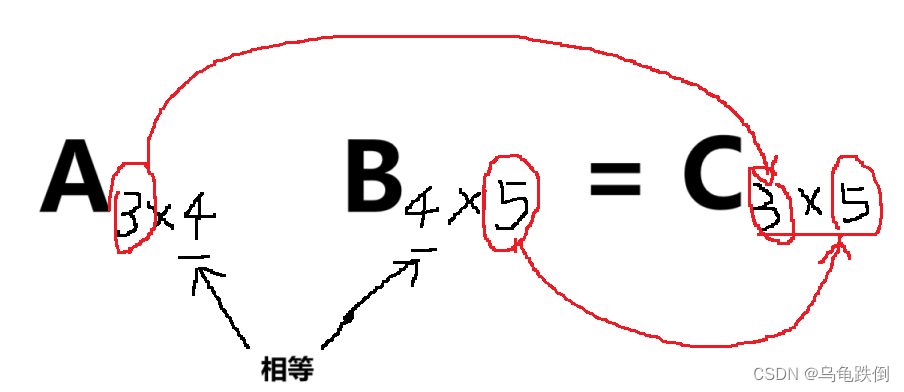
矩阵相乘的前提条件：第一个矩阵的列数等于第二个矩阵的行数。

结果矩阵的形状：结果矩阵的行等于第一个矩阵的行数，结果矩阵的列数等于第二个矩阵的列数。

宋氏七字：中间相等取两头！宋浩线代飞上天！

例如： $A_{2*3}$ * $A_{3*2}$ 的结果矩阵就是2*2的方阵。

这个实在太刁了，哥们忍不住吟诗一首：

咏宋浩七字口诀

【现】

不用动脑经，不用花一秒。

捏决拿咒间，单走一个6字。

中间相等两头取，宋浩线代飞上天！

从此不愁线代妖，可喜可贺上大分！

做两个小题目练练手：

$A_{99*55}$ * $B_{55*200}$ = $C_{99*200}$

$A_{s*h}$ * $B_{h * m}$ = $C_{s*m}$

2、矩阵乘法不满足的三条规律

1）AB != BA 一般不满足交换律

例如： $A_{5*2}$ $B_{2 *3}$ 可以相乘，满足中间相等。但是 $B_{2 *3}$ $A_{5*2}$ 就不可以，因为3和5中间不相等

矩阵乘法一般来说不满足交换，但是也存在交换的情况，此时满足AB = BA,这种情况叫做AB可交换

2）AB = 0 ，且A ！= 0 不能推出 B = 0

如果是数字运算中，xy = 0，可以推出x/y = 0；但是在矩阵运算中不可以

3）AB = AC ,且A ！= 0 不能推出B = C

同样的，在数字运算中，3x= 3y可以推出x=y，但是在矩阵运算中不可以

总结矩阵不满足的三条规律：

(1)AB ! = BA;

(2)AB = AC,A!=0 不能推出 B = C;

(3)AB = 0 不能推出A =0或B = 0;

（任何矩阵和0矩阵相乘都等于0矩阵，由于矩阵乘法的特殊性，需要注意0矩阵的形状）

3、矩阵乘法的运算规律

1）结合律 (AB)C = A(BC)

2)分配律 (A+B)C = AC + BC C(A+B) = CA + CB （注意，由于矩阵乘法的特殊性，矩阵的左右位置是有严格意义的，不能随意换，即矩阵的乘法不满足交换律）

3）k(AB) = (kA)B = A(kB) 对于一个数字来说，位置可以随意放置

（注意，对于上述三个运算规律来说，要保持矩阵乘法的先后位置，左乘和右乘的位置不能变）

4、矩阵的可交换

当AB = BA ，即A与B可以交换。当题目给你A与B可交换时，就在提醒你AB = BA

（相等矩阵：同型矩阵对应元素相等）

可交换的前提必须是同型方阵。

否则：例如 $A_{2*3}$ $B_{3*2}$ = $C_{2*2}$ AB的结果矩阵是2✖2的矩阵

$B_{3*2}$ $A_{2*3}$ = $C_{3*3}$ BA的结果矩阵式3✖3的矩阵

这里结果明显是不相等的！所以，如果不是同型方阵是不可以交换的。首先结果矩阵的形状就要出错

五、矩阵的幂运算

（注意：矩阵的幂运算必须是方阵,保证连续运算）

矩阵的幂运算： $A^{k}$ = AA...A

其中 $A^{_{0}}$ = E

性质1） $A^{^k{1}}$ $A^{k^{_{2}}}$ = $A^{^{k1 + k2}}$

性质2） $(A^{^{k1}})^{^{k2}}$ = $A^{^{k1k2}}$

(再次注意：矩阵的乘法不满足交换律)

$(AB)^{k^{}}$ ! = $A^{^{k}}B^{^{k}}$

例如： $(AB)^{^{2}}$ != $A^{_{2}}$ $B^{^{2}}$

为什么不相等？

因为： $(AB)^{^{2}}$ = ABAB

$A^{_{2}}$ $B^{^{2}}$ = AABB

我们永远要记住：矩阵的乘法不满足交换律，因此上式明显式不相等的。

除非AB可交换，即AB = BA.

同时：

$(A+B)^{^{2}}$ != $A^{_{2}}$ + 2AB + $B^{^{2}}$

证明：(A+B)(A+B) = (A+B)A + (A+B)B = $A^{_{2}}$ + BA + AB + $B^{^{2}}$

很明显，2AB ！= BA + AB

同理：

$(A-B)^{2^{}}$ != $A^{_{2}}$ - 2AB + $B^{^{2}}$

证明：(A-B)(A-B) = (A-B)A - (A-B)B = $A^{_{2}}$ - BA - AB + $B^{^{2}}$

很明显，2AB ！= -BA - AB

永远记住！！！！！！！

矩阵乘法要严格注意AB的先后位置，位置的变化是会影响运算结果的

（因为矩阵的乘法是第一个矩阵的行乘以第二个矩阵的列）

但是，对于 $(A + E)^{2^{}}$ = $A^{_{2}}$ + AE + EA + $B^{^{2}}$

$(A - E)^{2^{}}$ = $A^{_{2}}$ - AE - EA + $B^{^{2}}$

对于上两式来说，

任何矩阵乘以单位阵E的等于其本身，而对于单位阵来说，左乘和右乘是一样的。

故而，AE = EA , BE =EB

所以：

$(A + E)^{2^{}}$ = $A^{_{2}}$ + 2AE + $B^{^{2}}$

$(A - E)^{2^{}}$ = $A^{_{2}}$ - 2AE + $B^{^{2}}$

是成立的！

六、简单的矩阵运算，学到的知识点运用起来。

例如

给两个方程组：x1 = y1 -y2 y1 = z1 + z2 + z3

x2 = y1 + y2 y2 = z1 -2z2 + z3

要求x1 和 x2 用z1 z2 z3表示

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/weixin_40725706/article/detail/770177

推荐阅读

相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

闽ICP备14008679号