相机光学（十九）——像差理论（球差）_子午面和弧矢面图解

0.基本概念

在光学系统中，描述像差的方法主要有两种：波像差法和几何像差法。

波像差基于光的电磁波理论，借助波面进行研究。如果光学系统成完善像，则任一物点发出的球面波经过光学系统后在像空间应该是以高斯像点为秋心的球面波。也可以以高斯像作为成像参考，以物体发出的光线经过光学系统后其出身光纤相对于高斯像的偏差来衡量光学系统成像缺陷。

光学系统的近轴区具有理想的光学系统的性质，光学系统近轴区的成像被认为是理想像。实际光学系统所处的像和近轴区所称的像的差异即为像差。

光学系统对单色光成像时产生单色像差，单色光像差分为五类，球差，慧差，像散，场曲和畸变。对白光成像时，还额外产生两种色差，轴向色差和垂轴色差。

1.像差部分

（0）序言

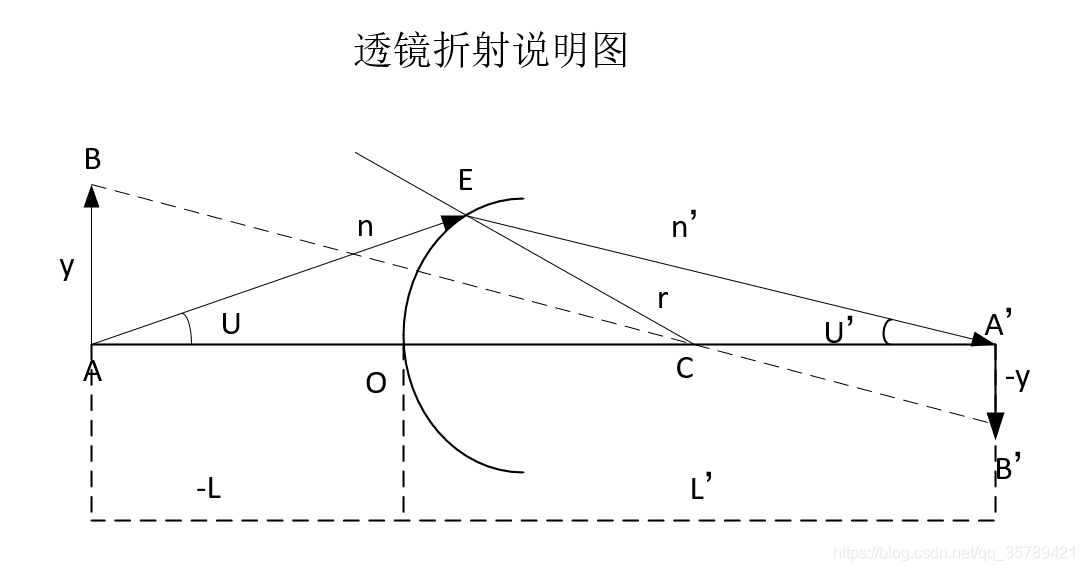
光线经单个折射球面的光路计算，是指在给定单个折射球面的结构参量n、n'、和r时，由已知入射光线L和U，计算折射后出射的参数L‘和U’。

如图所示，在三角形AEC中，应用正弦定理有：,可得球面上的入射角I为$sinI=\frac{L-r}{r}sinU$，由折射定律得，$sinI'=\frac{n}{n'}sinU$,根据外角关系，$∠EAC=$$\angle ECA=I+U=I'+U'$，故$U'=I+U-I'$，对于像方截距，$\frac{sinU'}{r}=\frac{sinI'}{L'-r}$,化简后可得，,这就是计算子午内光线光路的基本公式。

由于折射球面关于光轴旋转对称，对于光轴上点发出的任一条光线的光路，可以表示该光线绕光轴旋转一周所形成的锥面上全部光线的光路，显然这些光线在像方交光轴于同一点。当L为定值时，L'是U的函数。若发出同心光束，由于各光线具有不同的U，因而光束经球面折射后，将有不同的L'值，即失去了同心性。

（1）子午面、弧矢面、高斯面、入瞳面、出瞳面

<1>入瞳面、出瞳面

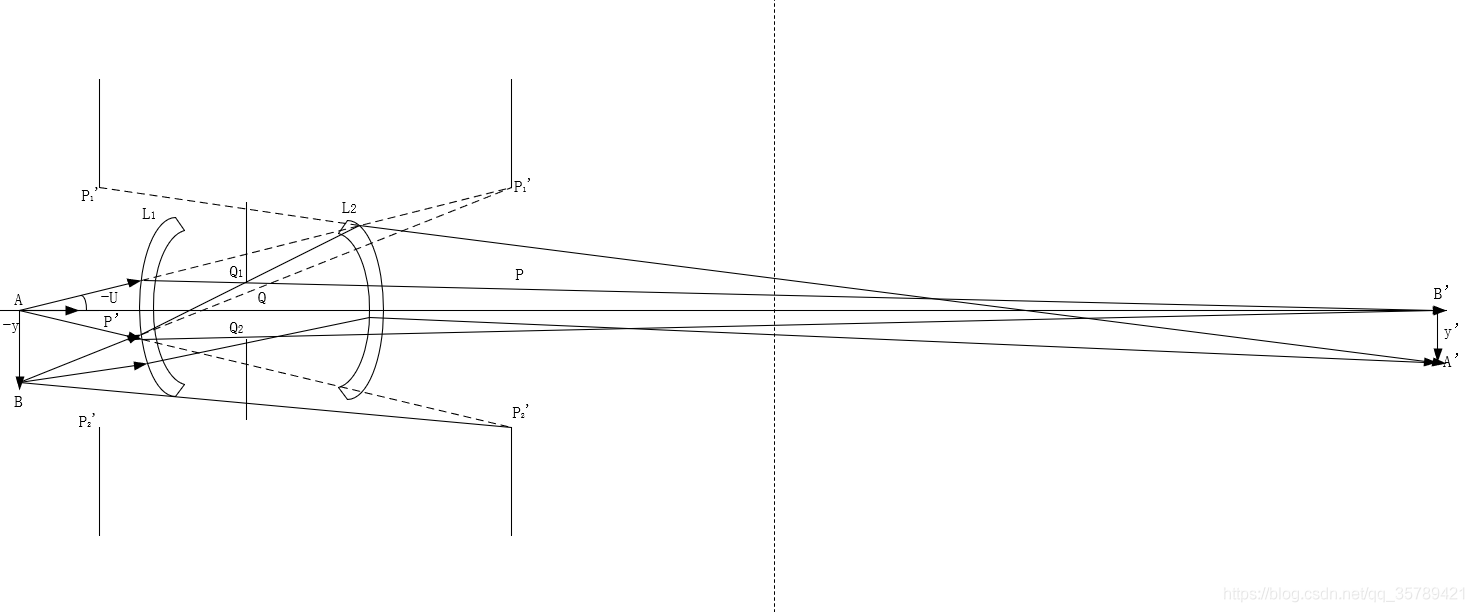
如图所示的光学系统有三个光阑，透镜L1成像到物空间，就是它本身；实际上起着限制光轴上物点的光束的作用，即为孔径光阑，孔径光阑在物空间的像称为入射光瞳。由物点发出经过入瞳边缘的光线与光轴的夹角，即成为光学系统的物方孔径角，此角即即为轴上点作边缘光线光路计算所取的孔径角。同理，把所有光阑通过其后面的光组成像到系统的像空间去。孔径光阑在系统像空间的像成为出射光瞳。

入射光瞳决定了能进入系统成像的最大光束孔径，并且是物面上各点发出并进入系统成像光束的公共入口。出瞳光瞳是物面上各点的成像光束经过系统后射出系统的公共出口。入射光瞳通过整个光学系统所成的像就是出射光瞳。如果孔径光阑在整个光学系统的像空间，它本身也就是出射光瞳，反之，在物空间，就是入射光瞳。

<2>子午面、弧矢面、高斯面

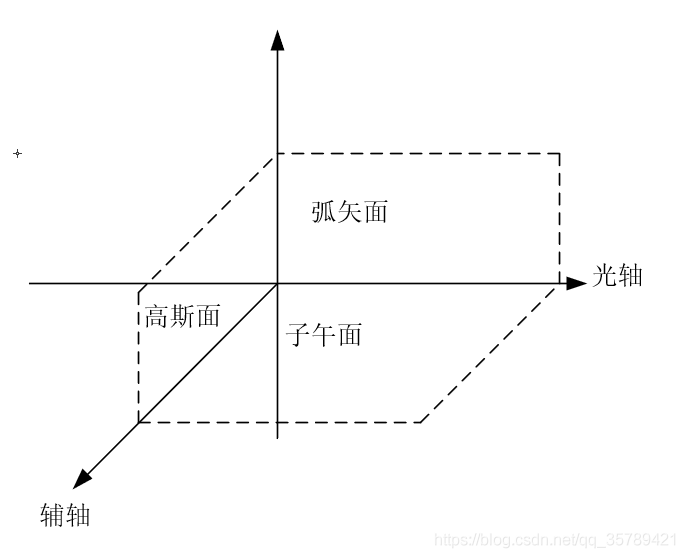
为了了解轴外物点所发出的充满入瞳的光束的结构和传播，可通过主光线取出两个互相垂直的截面，其中一个是主光线和光轴决定的平面，称为子午面；另一个是通过主光线和子午面垂直的截面，称为弧矢面。

(2)球差

自光轴上一点发出的光线，经球面折射后所得的像方截距L'是物方孔径角U或入射高度h的函数。因此，轴上点发出的同心光束经光束经光学系统各个球面折射以后，不再是同心光束，入射光线的孔径角U不同，其出射光线与光轴交点的位置就不同，相对于理想像点有不同的偏离。由于球差的存在，使得在高斯像面上得到的不是点像，而一个圆形弥散斑，也可以以弥散斑的半径表示球差，称为横向球差，高斯像面为轴向像差，$\delta T'=L'-l',\delta T'=\delta L'tanU'$。

球差是光轴上物点存在的唯一的一种单色像差，它与物点发出光线的物方孔径角有关。物方孔径角与光线在入瞳面上经过的点的位置有关。光学系统入瞳多为圆形，轴上点发出的光束在通过光学系统前、后均对称于光轴，所以子午面内光轴以上的光束的球差就可以表示物点发出的全部光束的球差。子午面内光轴以上一条光线的球差，实际上代表了与光轴有相同夹角的圆锥面上光束的球差，称为一个带光球差。

球差的存在，使得物点在高斯像面上成一个弥散斑，这将使像模糊不清。对于单透镜来说，光线的物方孔径角越大，球差量也越大单透镜不能校正球差，正透镜产生负球差，负透镜产生正球差。