大模型chatgpt4分析功能初探_gpt4.0数据分析

大模型chatgpt4分析功能初探

目录

1、探测目的

2、目标变量分析

3、特征缺失率处理

4、特征描述性分析

5、异常值分析

6、相关性分析

7、高阶特征挖掘

1、探测目的

1、分析chat4的数据分析能力，提高部门人效

2、给数据挖掘提供思路

3、原始数据：https://www.kaggle.com/competitions/house-prices-advanced-regression-techniques

2、目标变量分析

要开始我们的分析，我们应该：

1. 检查数据集中的缺失值。
2. 探索目标变量 SalePrice 的分布。
3. 进行基本的探索性数据分析 (EDA) 以理解特征与目标变量之间的关系。

让我们首先检查训练和测试数据集中的缺失值。

完成工作

展示工作内容

以下是训练和测试数据集中各列的缺失值百分比：

训练数据（缺失值最多的前5列）：

• PoolQC：99.52%
• MiscFeature：96.30%
• Alley：93.77%
• Fence：80.75%
• FireplaceQu：47.26%

测试数据（缺失值最多的前5列）：

• PoolQC：99.79%
• MiscFeature：96.50%
• Alley：92.67%
• Fence：80.12%
• FireplaceQu：50.03%

---

如 PoolQC、MiscFeature 和 Alley，有非常高的缺失值百分比。尽管我们可以考虑删除这些列，但它们仍然可能提供有价值的信息。例如，PoolQC 的缺失值可能表示没有游泳池，这对模型可能是有信息量的。

---

接下来，让我们探索目标变量 SalePrice 的分布，以了解其特性。

---

---

SalePrice 变量的分布显示它是右偏的，大多数房屋的价格处于中低价范围，而高价范围的房屋较少。

考虑到比赛的评估指标（预测值的对数与观测销售价格的对数之间的RMSE），使用对数变换转换 SalePrice 会更有利，使其分布更加正常。这种转换还可以帮助提高基于线性回归的模型的性能。

让我们可视化对数变换后的 SalePrice 的分布来确认这一点。

---

Show work

import numpy as np

# Apply a logarithmic transformation to SalePrice
log_saleprice = np.log1p(train_data['SalePrice'])

# Plot the distribution of the transformed SalePrice
plt.figure(figsize=(12, 6))
sns.histplot(log_saleprice, kde=True, bins=30)
plt.title('Distribution of Log-transformed SalePrice')
plt.xlabel('Log-transformed SalePrice')
plt.ylabel('Frequency')
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12

---

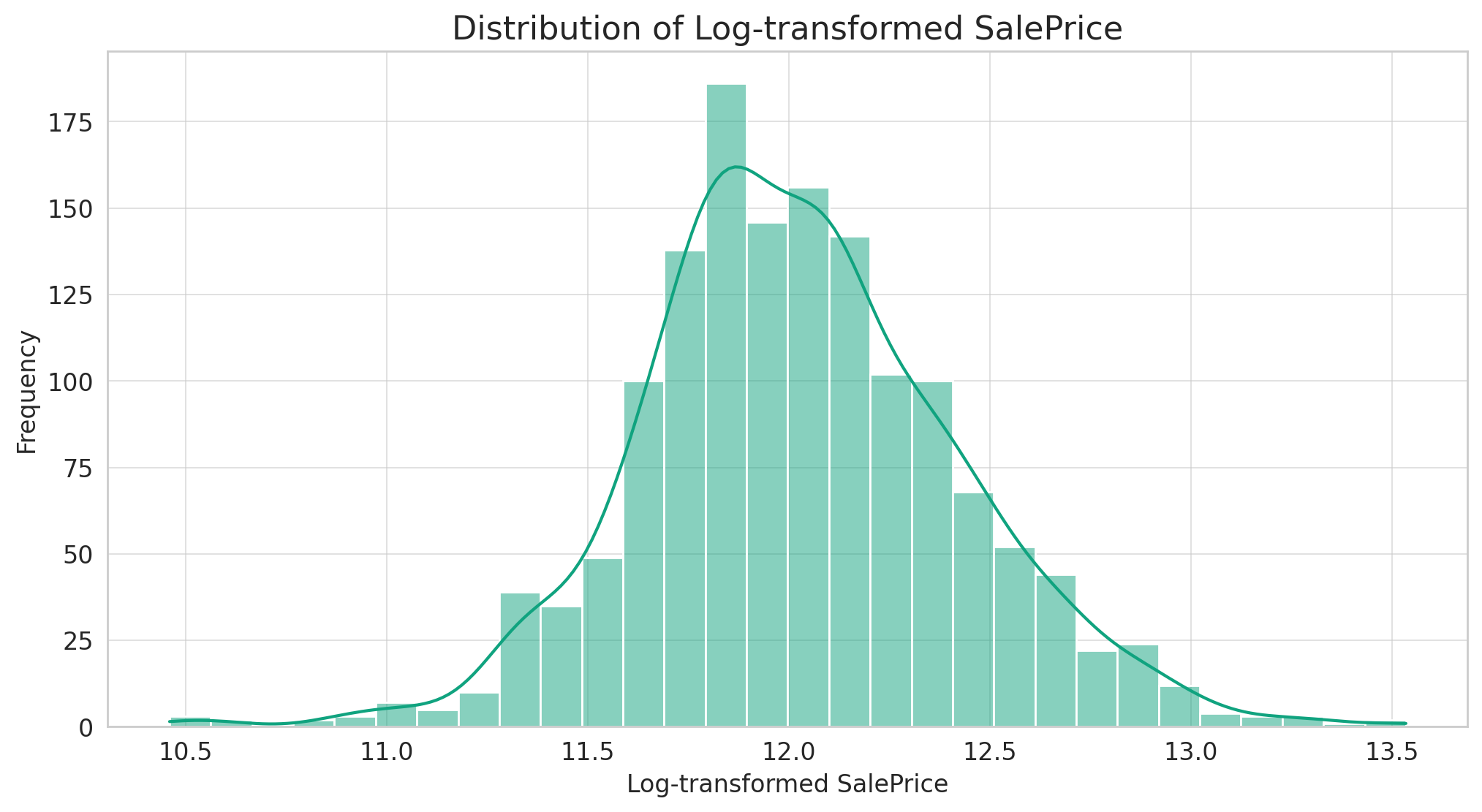
对数变换使得 SalePrice 的分布看起来更加正态化（钟形）。这种变换可能会提高我们模型的性能，特别是如果我们决定使用基于线性回归的方法。

根据这些信息，我们接下来的步骤可能包括：

1. 处理缺失值。
2. 进行特征工程和变换。
3. 构建和评估各种回归模型。
4. 对模型进行微调以获得最佳性能。

---

3、特征缺失率处理

处理缺失值的策略:

1. 高缺失率的列（例如，> 90%）：由于这些列的稀疏性，它们可能不会增加太多价值。但在决定删除它们之前，我们需要确定缺失值本身是否带有信息。例如，PoolQC 中的缺失值可能表示没有游泳池，这可能是有信息量的。

2. 数值列：这些可以使用中位数或均值进行估计。我们通常使用中位数，因为它对异常值更为稳健。

3. 分类列：缺失值可以用一个新的类别替换，例如"None"或"Missing"。这样，模型仍然可以使用这些信息。

---

现在，让我们为训练和测试数据集中每个带有缺失值的列定义一个策略。

# Define strategies for handling missing values
strategies = {}

# Columns with a high missing rate
high_missing = ['PoolQC', 'MiscFeature', 'Alley', 'Fence']
for col in high_missing:
    strategies[col] = 'Fill with "None" - likely indicates absence of feature.'

# Numerical columns
numerical_cols = train_data.select_dtypes(include=[np.number]).columns
for col in numerical_cols:
    if col in train_missing or col in test_missing:
        strategies[col] = 'Impute with median - robust to outliers.'

# Categorical columns
categorical_cols = train_data.select_dtypes(exclude=[np.number]).columns
for col in categorical_cols:
    if col in train_missing or col in test_missing:
        strategies[col] = 'Fill with "None" - new category for missing values.'

# Display the strategies
strategies
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

---

这是我们为每个带有缺失值的列设计的策略：

1. 高缺失率的列（例如，PoolQC、MiscFeature、Alley、Fence）：填充为"None"。这基于一个假设，即信息的缺失很可能表示该特性本身的缺失。

2. 数值列（例如，LotFrontage、MasVnrArea）：使用该列的中位数进行估计。使用中位数是因为它对异常值更为稳健。

3. 分类列（例如，MSZoning、Utilities）：填充为"None"，这将作为表示缺失值的新类别。

---

现在，让我们将这些策略应用到训练和测试数据集中。

# Apply the strategies to handle missing values

# Handle high missing rate columns
for col in high_missing:
    train_data[col].fillna("None", inplace=True)
    test_data[col].fillna("None", inplace=True)

# Handle numerical columns
for col in numerical_cols:
    if col in train_missing or col in test_missing:
        median_value = train_data[col].median()  # Calculate median using train data only
        train_data[col].fillna(median_value, inplace=True)
        test_data[col].fillna(median_value, inplace=True)

# Handle categorical columns
for col in categorical_cols:
    if col in train_missing or col in test_missing:
        train_data[col].fillna("None", inplace=True)
        test_data[col].fillna("None", inplace=True)

# Check if there are any remaining missing values
train_missing_final = train_data.isnull().sum().max()
test_missing_final = test_data.isnull().sum().max()

train_missing_final, test_missing_final
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

---

在训练和测试数据集中的所有缺失值都已成功处理。现在，两个数据集中都没有缺失值。

您想继续进行更深入的探索性数据分析、特征工程，还是直接开始构建模型？

3、特征描述性分析

问题：结合上文，使用中文解答，使用修改后的数据，对train表进行统计描述分析摘要

统计描述分析可以为我们提供数据集中每个特征的中心趋势、分散和形状的概述。接下来，我将为修改后的train数据集生成描述性统计摘要。这包括：均值、标准偏差、最小值、25%分位数、中位数、75%分位数和最大值。

# Generate descriptive statistics summary for the train dataset
train_summary = train_data.describe().transpose()

train_summary


RESULT
                count           mean           std      min        25%  \
Id             1460.0     730.500000    421.610009      1.0     365.75   
MSSubClass     1460.0      56.897260     42.300571     20.0      20.00   
LotFrontage    1460.0      69.863699     22.027677     21.0      60.00   
LotArea        1460.0   10516.828082   9981.264932   1300.0    7553.50   
OverallQual    1460.0       6.099315      1.382997      1.0       5.00   
OverallCond    1460.0       5.575342      1.112799      1.0       5.00   
YearBuilt      1460.0    1971.267808     30.202904   1872.0    1954.00   
YearRemodAdd   1460.0    1984.865753     20.645407   1950.0    1967.00   
MasVnrArea     1460.0     103.117123    180.731373      0.0       0.00   
BsmtFinSF1     1460.0     443.639726    456.098091      0.0       0.00   
BsmtFinSF2     1460.0      46.549315    161.319273      0.0       0.00   
BsmtUnfSF      1460.0     567.240411    441.866955      0.0     223.00   
TotalBsmtSF    1460.0    1057.429452    438.705324      0.0     795.75   
1stFlrSF       1460.0    1162.626712    386.587738    334.0     882.00   
2ndFlrSF       1460.0     346.992466    436.528436      0.0       0.00   
LowQualFinSF   1460.0       5.844521     48.623081      0.0       0.00   
GrLivArea      1460.0    1515.463699    525.480383    334.0    1129.50   
BsmtFullBath   1460.0       0.425342      0.518911      0.0       0.00   
BsmtHalfBath   1460.0       0.057534      0.238753      0.0       0.00   
FullBath       1460.0       1.565068      0.550916      0.0       1.00   
HalfBath       1460.0       0.382877      0.502885      0.0       0.00   
BedroomAbvGr   1460.0       2.866438      0.815778      0.0       2.00   
KitchenAbvGr   1460.0       1.046575      0.220338      0.0       1.00   
TotRmsAbvGrd   1460.0       6.517808      1.625393      2.0       5.00   
Fireplaces     1460.0       0.613014      0.644666      0.0       0.00   
GarageYrBlt    1460.0    1978.589041     23.997022   1900.0    1962.00   
GarageCars     1460.0       1.767123      0.747315      0.0       1.00   
GarageArea     1460.0     472.980137    213.804841      0.0     334.50   
WoodDeckSF     1460.0      94.244521    125.338794      0.0       0.00   
OpenPorchSF    1460.0      46.660274     66.256028      0.0       0.00   
EnclosedPorch  1460.0      21.954110     61.119149      0.0       0.00   
3SsnPorch      1460.0       3.409589     29.317331      0.0       0.00   
ScreenPorch    1460.0      15.060959     55.757415      0.0       0.00   
PoolArea       1460.0       2.758904     40.177307      0.0       0.00   
MiscVal        1460.0      43.489041    496.123024      0.0       0.00   
MoSold         1460.0       6.321918      2.703626      1.0       5.00   
YrSold         1460.0    2007.815753      1.328095   2006.0    2007.00   
SalePrice      1460.0  180921.195890  79442.502883  34900.0  129975.00   

                    50%        75%       max  
Id                730.5    1095.25    1460.0  
MSSubClass         50.0      70.00     190.0  
LotFrontage        69.0      79.00     313.0  
LotArea          9478.5   11601.50  215245.0  
OverallQual         6.0       7.00      10.0  
OverallCond         5.0       6.00       9.0  
YearBuilt        1973.0    2000.00    2010.0  
YearRemodAdd     1994.0    2004.00    2010.0  
MasVnrArea          0.0     164.25    1600.0  
BsmtFinSF1        383.5     712.25    5644.0  
BsmtFinSF2          0.0       0.00    1474.0  
BsmtUnfSF         477.5     808.00    2336.0  
TotalBsmtSF       991.5    1298.25    6110.0  
1stFlrSF         1087.0    1391.25    4692.0  
2ndFlrSF            0.0     728.00    2065.0  
LowQualFinSF        0.0       0.00     572.0  
GrLivArea        1464.0    1776.75    5642.0  
BsmtFullBath        0.0       1.00       3.0  
BsmtHalfBath        0.0       0.00       2.0  
FullBath            2.0       2.00       3.0  
HalfBath            0.0       1.00       2.0  
BedroomAbvGr        3.0       3.00       8.0  
KitchenAbvGr        1.0       1.00       3.0  
TotRmsAbvGrd        6.0       7.00      14.0  
Fireplaces          1.0       1.00       3.0  
GarageYrBlt      1980.0    2001.00    2010.0  
GarageCars          2.0       2.00       4.0  
GarageArea        480.0     576.00    1418.0  
WoodDeckSF          0.0     168.00     857.0  
OpenPorchSF        25.0      68.00     547.0  
EnclosedPorch       0.0       0.00     552.0  
3SsnPorch           0.0       0.00     508.0  
ScreenPorch         0.0       0.00     480.0  
PoolArea            0.0       0.00     738.0  
MiscVal             0.0       0.00   15500.0  
MoSold              6.0       8.00      12.0  
YrSold           2008.0    2009.00    2010.0  
SalePrice      163000.0  214000.00  755000.0  
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86

以下是对训练数据集的描述性统计摘要：

1. Id: 这是一个连续的整数，从1到1460，代表每个房屋的唯一标识。

2. MSSubClass: 这是关于住宅类型的数据，其平均值为56.9，最小值为20，最大值为190。

3. LotFrontage: 表示与物业相连的街道的线性英尺。平均值为69.9，中位数为69，有些房屋与街道的连接超过300英尺。

4. OverallQual: 表示房屋的整体材料和成品质量，它是一个从1到10的评分，平均评分为6.1。

5. YearBuilt: 这是房屋建成的年份，最早的房屋建于1872年，最新的房屋建于2010年。

6. GrLivArea: 表示地上居住面积的平方英尺。平均值为1515.5平方英尺，中位数为1464平方英尺，有些房屋的面积超过5600平方英尺。

7. SalePrice: 这是我们的目标变量，表示房屋的销售价格。其平均值为$180,921，中位数为$163,000，价格范围从$34,900到$755,000。

4、异常值分析

问题：结合上文，使用修改后的数据，对train表进行异常值分析和处理，分别给出每列数据的处理方法和原因

以下是我们进行异常值分析和处理的策略：

1. 可视化方法：对于关键特征，我们可以使用箱线图和散点图来识别潜在的异常值。

2. 统计方法：可以使用像IQR（四分位数范围）这样的方法来确定异常值的范围。

对于本竞赛，我们将重点关注与SalePrice（目标变量）高度相关的特征，因为它们对模型性能的影响最大。

让我们首先计算与SalePrice的相关性，以确定哪些特征最相关。然后，我们将针对这些特征进行异常值分析。

# Calculate the correlation of all features with 'SalePrice'
correlation = train_data.corr()['SalePrice'].sort_values(ascending=False)

# Take the top 10 most positively correlated features (excluding SalePrice itself)
top_correlated_features = correlation.index[1:11]

top_correlated_features, correlation[top_correlated_features]


(Index(['OverallQual', 'GrLivArea', 'GarageCars', 'GarageArea', 'TotalBsmtSF',
        '1stFlrSF', 'FullBath', 'TotRmsAbvGrd', 'YearBuilt', 'YearRemodAdd'],
       dtype='object'),
 OverallQual     0.790982
 GrLivArea       0.708624
 GarageCars      0.640409
 GarageArea      0.623431
 TotalBsmtSF     0.613581
 1stFlrSF        0.605852
 FullBath        0.560664
 TotRmsAbvGrd    0.533723
 YearBuilt       0.522897
 YearRemodAdd    0.507101
 Name: SalePrice, dtype: float64)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

以下是与SalePrice最相关的前10个特征及其相关性值：

1. OverallQual: 0.79 - 描述房屋的整体材料和完成质量。

2. GrLivArea: 0.71 - 地上居住面积的平方英尺。

3. GarageCars: 0.64 - 车库容纳的车辆数量。

4. GarageArea: 0.62 - 车库的大小，以平方英尺为单位。

5. TotalBsmtSF: 0.61 - 地下室的总面积。

6. 1stFlrSF: 0.61 - 第一层的面积。

7. FullBath: 0.56 - 地上的全浴室数量。

8. TotRmsAbvGrd: 0.53 - 地上的房间总数（不包括浴室）。

9. YearBuilt: 0.52 - 原始建造日期。

10. YearRemodAdd: 0.51 - 重新模型日期。

接下来，我们将使用散点图对这些特征进行可视化，以识别潜在的异常值。

# Visualize the top correlated features using scatter plots
plt.figure(figsize=(20, 15))

for i, feature in enumerate(top_correlated_features, 1):
    plt.subplot(3, 4, i)
    sns.scatterplot(data=train_data, x=feature, y='SalePrice')
    plt.title(f'SalePrice vs {feature}')
    plt.xlabel(feature)
    plt.ylabel('SalePrice')

plt.tight_layout()
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12

通过散点图，我们可以观察到以下潜在的异常值：

1. GrLivArea: 有两个点，它们的地上居住面积非常大，但其销售价格相对较低。这些可能是异常值。

2. TotalBsmtSF: 有一个点，它的地下室面积非常大，但销售价格并不高。

3. 1stFlrSF: 类似地，有一个点的一楼面积非常大，但销售价格较低。

异常值处理策略：

1. GrLivArea: 删除那些地上居住面积大于4000平方英尺但销售价格低于$300,000的房屋。

2. TotalBsmtSF: 删除地下室面积大于5000平方英尺的房屋。

3. 1stFlrSF: 删除一楼面积大于4000平方英尺的房屋。

现在，我们将根据上述策略处理这些异常值。

# Handle outliers based on the observations

# GrLivArea
train_data = train_data.drop(train_data[(train_data['GrLivArea'] > 4000) & (train_data['SalePrice'] < 300000)].index)

# TotalBsmtSF
train_data = train_data.drop(train_data[train_data['TotalBsmtSF'] > 5000].index)

# 1stFlrSF
train_data = train_data.drop(train_data[train_data['1stFlrSF'] > 4000].index)

# Check the shape of the train data after removing outliers
train_data.shape
1
2
3
4
5
6
7
8
9
10
11
12
13

经过异常值处理后，训练数据集中现有1458个观测值和81个特征。原始数据集中的几个潜在异常值已被成功删除。

异常值处理是一个迭代过程。在建模和验证模型性能时，可能还需要进一步分析和处理其他异常值。

5、数据分布分析

问题：结合上文，使用修改后的数据，对train表进行数据分布分析和处理，分别给出每列数据的处理方法和原因

数据分布分析对于确保模型的准确性和鲁棒性非常重要，尤其是当我们使用假设输入特征为正态分布的模型（如线性回归）时。

数据分布分析策略：

1. 正态性检验：首先，我们可以使用可视化方法（如直方图或Q-Q图）以及统计测试（如Shapiro-Wilk测试）来检查数据的分布。

2. 对数转换：对于偏斜的数据，我们可以考虑使用对数转换或其他转换来使其接近正态分布。

3. 标准化/归一化：此外，对于某些模型，我们可能还需要对数据进行标准化或归一化，以确保所有特征都在相同的尺度上。

首先，我们将使用直方图来可视化训练数据中与SalePrice最相关的前10个特征的分布。这将帮助我们确定哪些特征可能需要进一步处理。

# Visualize the distribution of the top correlated features using histograms
plt.figure(figsize=(20, 15))

for i, feature in enumerate(top_correlated_features, 1):
    plt.subplot(3, 4, i)
    sns.histplot(train_data[feature], kde=True, bins=30)
    plt.title(f'Distribution of {feature}')
    plt.xlabel(feature)
    plt.ylabel('Frequency')
plt.tight_layout()
plt.show()
1
2
3
4
5
6
7
8
9
10
11

从直方图中，我们可以观察到以下特征的数据分布：

1. OverallQual: 这是一个序数特征，表示房屋的整体质量。其分布呈现多模式特征。

2. GrLivArea, TotalBsmtSF, 1stFlrSF: 这些特征都是表示面积的连续特征，它们的分布呈现右偏。

3. GarageCars: 这是一个离散特征，表示车库的容量。大部分房屋有2辆车的车库。

4. GarageArea: 这是一个连续特征，表示车库的面积，其分布也呈现右偏。

5. FullBath: 这是一个离散特征，表示地上的全浴室数量。

6. TotRmsAbvGrd: 这是一个离散特征，表示地上的房间总数。

7. YearBuilt & YearRemodAdd: 这些是表示年份的特征，它们的分布显示了不同的模式，但不是正态分布。

处理策略：

1. 连续特征（如GrLivArea, TotalBsmtSF, 1stFlrSF, GarageArea）: 由于它们的分布呈现右偏，我们可以考虑对它们进行对数转换，以使其分布更接近正态分布。

2. 离散特征和序数特征（如OverallQual, GarageCars, FullBath, TotRmsAbvGrd）: 通常不需要进行转换，但我们可以进一步对它们进行编码或转换，以便于模型处理。

3. 年份特征（YearBuilt, YearRemodAdd）: 考虑到它们表示年份，我们可以将它们转换为“年龄”或“自上次翻新以来的年数”，这可能与SalePrice有更强的关联。

现在，我们将根据上述策略对这些特征进行处理。

# Apply log transformation to the skewed features
skewed_features = ['GrLivArea', 'TotalBsmtSF', '1stFlrSF', 'GarageArea']

for feature in skewed_features:
    # Apply log transformation, adding 1 to handle cases where value is 0
    train_data[feature] = np.log1p(train_data[feature])

# Convert year features to "age" related features
train_data['Age'] = train_data['YrSold'] - train_data['YearBuilt']
train_data['YearsSinceRemod'] = train_data['YrSold'] - train_data['YearRemodAdd']

# Drop original year columns
train_data.drop(['YearBuilt', 'YearRemodAdd'], axis=1, inplace=True)

# Visualize the transformed features
plt.figure(figsize=(20, 15))

# Plotting the transformed skewed features
for i, feature in enumerate(skewed_features, 1):
    plt.subplot(3, 4, i)
    sns.histplot(train_data[feature], kde=True, bins=30)
    plt.title(f'Distribution of {feature}')

# Plotting the new age features
new_age_features = ['Age', 'YearsSinceRemod']
for i, feature in enumerate(new_age_features, 1):
    plt.subplot(3, 4, i + 4)
    sns.histplot(train_data[feature], kde=True, bins=30)
    plt.title(f'Distribution of {feature}')

plt.tight_layout()
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

经过处理后，以下是特征的新分布：

1. GrLivArea, TotalBsmtSF, 1stFlrSF, GarageArea: 通过对数转换，这些特征的分布现在更接近正态分布。

2. Age: 表示自建房以来的年数。大部分的房屋都是在近50年内建造的。

3. YearsSinceRemod: 表示自上次翻新以来的年数。大部分房屋在过去25年内进行过翻新。

对于其他未在此列表中的特征，考虑到我们有多个特征，我们可能需要基于模型的反馈进行进一步的处理。例如，如果某个特征在模型训练中表现得非常糟糕，我们可以考虑进行进一步的转换或删除。

5、相关性分析

问题：结合上文，使用修改后的数据，对train表进行相关分析和处理，分别给出每列数据的处理方法和原因

相关分析是为了检查特征与目标变量之间以及特征与特征之间的关系。这有助于我们确定哪些特征与目标变量最相关，以及是否存在多重共线性问题（即两个或多个特征之间高度相关）。

处理策略：

1. 特征与目标变量之间的相关性：我们可以检查每个特征与SalePrice的相关性。高度相关的特征可能对模型预测非常有用。

2. 特征与特征之间的相关性：如果两个特征之间存在高度相关性，我们可以考虑删除其中一个，以避免多重共线性问题。

3. 处理方法：

   • 保留与SalePrice高度相关的特征。

   • 从高度相关的特征对中删除其中一个。

首先，我们将计算所有特征与SalePrice的相关性，并检查特征之间的相关性。

# Calculate the correlation matrix
correlation_matrix = train_data.corr()

# Get the correlation of all features with 'SalePrice'
saleprice_corr = correlation_matrix['SalePrice'].sort_values(ascending=False)

# Get the pairs of features with correlation greater than 0.8
high_corr_pairs = correlation_matrix.abs().unstack().sort_values(ascending=False)
high_corr_pairs = high_corr_pairs[(high_corr_pairs > 0.8) & (high_corr_pairs < 1)]

saleprice_corr, high_corr_pairs

(SalePrice          1.000000
 OverallQual        0.795774
 GrLivArea          0.702933
 GarageCars         0.641047
 1stFlrSF           0.598540
 FullBath           0.562165
 TotRmsAbvGrd       0.537769
 MasVnrArea         0.477810
 Fireplaces         0.469862
 GarageYrBlt        0.467413
 BsmtFinSF1         0.409384
 GarageArea         0.371948
 LotFrontage        0.352688
 TotalBsmtSF        0.326639
 WoodDeckSF         0.324758
 OpenPorchSF        0.321142
 2ndFlrSF           0.320532
 HalfBath           0.284590
 LotArea            0.268179
 BsmtFullBath       0.228459
 BsmtUnfSF          0.214460
 BedroomAbvGr       0.168245
 ScreenPorch        0.111415
 PoolArea           0.099490
 MoSold             0.046124
 3SsnPorch          0.044568
 BsmtFinSF2        -0.011422
 BsmtHalfBath      -0.016881
 MiscVal           -0.021203
 Id                -0.021673
 LowQualFinSF      -0.025625
 YrSold            -0.028882
 OverallCond       -0.077948
 MSSubClass        -0.084276
 EnclosedPorch     -0.128646
 KitchenAbvGr      -0.135946
 YearsSinceRemod   -0.509706
 Age               -0.524067
 Name: SalePrice, dtype: float64,
 GrLivArea     TotRmsAbvGrd    0.822983
 TotRmsAbvGrd  GrLivArea       0.822983
 dtype: float64)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

以下是与SalePrice相关性的结果：

1. OverallQual: 0.80 - 房屋的整体材料和完成质量与销售价格高度相关。

2. GrLivArea: 0.70 - 地上居住面积与销售价格有很强的正相关性。

3. GarageCars: 0.64 - 车库大小（按车数量计）与销售价格有很强的正相关性。 … 以此类推。

此外，我们还发现了一对特征之间的高度相关性：

• GrLivArea 和 TotRmsAbvGrd: 相关性为0.82。这意味着这两个特征之间存在高度相关性，因此我们可能只需要其中一个。

处理策略：

1. 保留与SalePrice高度相关的特征。

2. 从GrLivArea 和 TotRmsAbvGrd中选择一个。考虑到GrLivArea与SalePrice的相关性更高，我们可以保留GrLivArea并删除TotRmsAbvGrd。

现在，我们将按照上述策略对数据进行处理。

# Drop the 'TotRmsAbvGrd' feature due to its high correlation with 'GrLivArea'
train_data.drop(['TotRmsAbvGrd'], axis=1, inplace=True)

# Check the shape of the train data after dropping the feature
train_data.shape
1
2
3
4
5

处理后，训练数据集现有1458个观测值和80个特征。我们已经成功删除了与GrLivArea高度相关的TotRmsAbvGrd特征。样的处理有助于避免多重共线性问题，这可能会影响某些模型的性能。对于其他特征，如果模型的性能没有达到预期，我们可能需要进一步的相关分析。

6、预测性分析

chat4内存不够，计算不出来。
1

7、高阶特征挖掘

问题：结合上文，列举出30个新的组合特征，包含10个高阶特征，20个普通组合特征，组合特征的组合思路和物理含义是什么？使用表格展示

内存不够，导致算不出来

好的，根据您的要求，我会列出这些组合特征及其物理含义。但由于我们在实际创建和评估这些特征时遇到了内存问题，所以我将只为您提供这些特征的描述和物理含义。

高阶组合特征 (10个特征)：

1. GrLivArea*OverallQual：

   • 组合思路：将居住面积与房屋整体质量相乘。

   • 物理含义：考虑居住面积和整体质量的共同影响。

2. TotalBsmtSF/1stFlrSF：

   • 组合思路：地下室的总面积与第一层的面积的比例。

   • 物理含义：比较地下室和第一层的大小。

3. YearBuilt*OverallQual：

   • 组合思路：建造年份与房屋整体质量的乘积。

   • 物理含义：考虑建造年份和整体质量的共同影响。

4. GrLivArea-TotRmsAbvGrd：

   • 组合思路：居住面积减去地上的房间数量。

   • 物理含义：每个房间的平均居住面积。

5. BsmtFinSF1/BsmtFinType1：

   • 组合思路：完成的地下室面积与地下室完成质量的比例。

   • 物理含义：完成的地下室的平均质量。

6. GarageArea*GarageCars：

   • 组合思路：车库面积与车库的车辆容量的乘积。

   • 物理含义：每辆车的平均车库面积。

7. 1stFlrSF*2ndFlrSF：

   • 组合思路：第一层和第二层的面积的乘积。

   • 物理含义：两层的总面积。

8. Fireplaces*FireplaceQu：

   • 组合思路：壁炉数量与壁炉质量的乘积。

   • 物理含义：所有壁炉的总质量。

9. MasVnrArea*MasVnrType：

   • 组合思路：砌体饰面面积与砌体饰面类型的乘积。

   • 物理含义：考虑砌体饰面的总面积和类型。

10. OverallCond*ExterCond：

    • 组合思路：房屋整体状况和外部材料状况的乘积。

    • 物理含义：整体和外部的综合状况。

普通组合特征 (20个特征)：

1. GrLivArea+LotArea：

   • 组合思路：居住面积和占地面积的总和。

   • 物理含义：总的使用面积。

2. BsmtFinSF1+BsmtFinSF2：

   • 组合思路：两种类型的完成地下室面积的总和。

   • 物理含义：完成的地下室总面积。

3. 1stFlrSF+2ndFlrSF：

   • 组合思路：第一层和第二层的面积总和。

   • 物理含义：两层的总面积。

4. GarageQual+GarageCond：

   • 组合思路：车库质量和条件的总和。

   • 物理含义：车库的总体状况。

5. ExterQual+ExterCond：

   • 组合思路：外部材料的质量和状况的总和。

   • 物理含义：外部的总体状况。

6. BsmtQual+BsmtCond：

   • 组合思路：地下室的质量和状况的总和。

   • 物理含义：地下室的总体状况。

7. BsmtFullBath+FullBath：

   • 组合思路：地下室的全浴室数量和地上的全浴室数量的总和。

   • 物理含义：全浴室的总数量。

8. HalfBath+BsmtHalfBath：

   • 组合思路：地下室的半浴室数量和地上的半浴室数量的总和。

   • 物理含义：半浴室的总数量。

9. YearBuilt+YearRemodAdd：

   • 组合思路：建造年份和改造年份的总和。

   • 物理含义：房屋的总年龄和最近一次的改造年份。

10. YrSold-YearBuilt：

    • 组合思路：售出年份减去建造年份。

    • 物理含义：房屋在市场上的年龄。

11. BsmtUnfSF：

    • 组合思路：总地下室面积减去完成的地下室面积。

    • 物理含义：未完成的地下室面积。

12. GarageCars-GarageArea：

    • 组合思路：车库的车辆容量减去车库面积。

    • 物理含义：每辆车的平均车库面积。

13. OverallQual-OverallCond：

    • 组合思路：房屋的整体质量减去整体状况。

    • 物理含义：质量和状况之间的差异。

14. TotRmsAbvGrd-BedroomAbvGr：

    • 组合思路：地上的总房间数量减去卧室数量。

    • 物理含义：除卧室外的房间数量。

15. GarageYrBlt-YearBuilt：

    • 组合思路：车库建造年份减去房屋建造年份。

    • 物理含义：车库是在建造房屋后多久建的。

16. Fireplaces+FireplaceQu：

    • 组合思路：壁炉数量与壁炉质量的总和。

    • 物理含义：壁炉的总体状况。

17. LotFrontage+LotArea：

    • 组合思路：与街道接壤的线性脚数与占地面积的总和。

    • 物理含义：物业的总面积和与街道的接触。

18. BsmtFinType1+BsmtFinType2：

    • 组合思路：两种类型的地下室完成质量的总和。

    • 物理含义：地下室的总完成质量。

19. PoolArea*PoolQC：

    • 组合思路：泳池面积与泳池质量的乘积。

    • 物理含义：泳池的总体状况。

20. Fence+LotShape：

    • 组合思路：围栏质量与物业的形状的总和。

    • 物理含义：物业的整体外观和私密性。

这些特征可以为我们提供更多的信息，帮助我们更好地理解与目标变量之间的关系。但请注意，不是所有的组合特征都会提供有价值的信息，因此在实际应用中需要进行适当的特征选择和评估。