山东大学机器学习实验3

在本练习中，您将使用牛顿方法来实现一个分类问题上的逻辑回归。请下载ex4Data.zip并从zip文件中提取文件。在这个练习中，假设一所高中有一个数据集，它代表了40名被大学录取的学生和40名未被录取的学生。每个(x(i）、y(i））培训示例都包含一个学生在两个标准化考试中的分数，以及一个学生是否被录取的标签。你的任务是建立一个二元分类模型，根据学生在两场考试中的分数来估计大学录取机会。

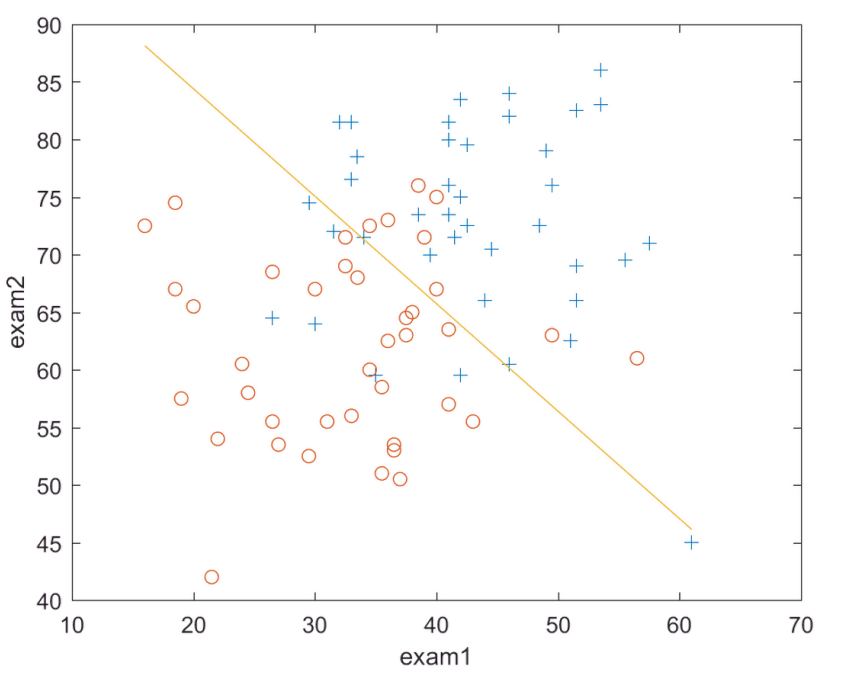
决策边界如图所示：

在决策边界上方表示正类，被录取。

在决策边界下方表示负类，未被录取。

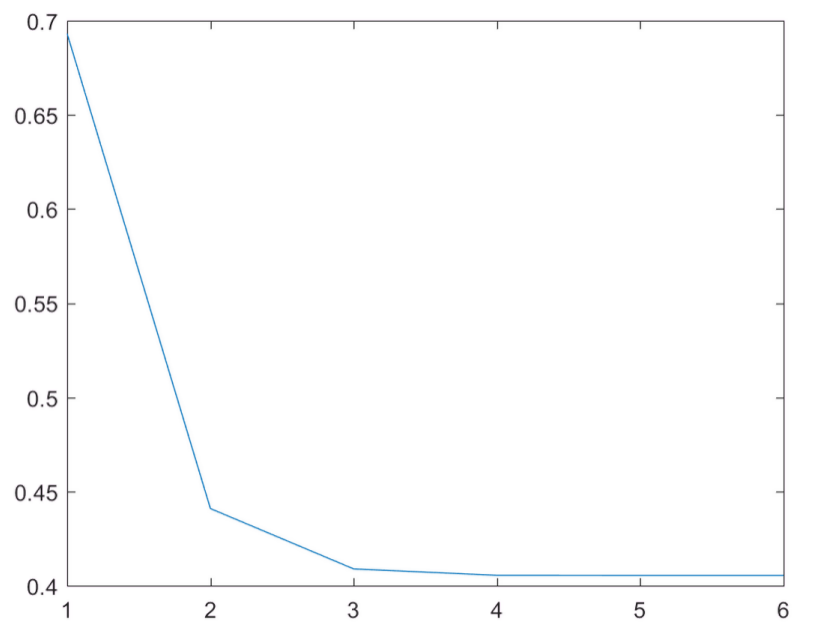
损失函数在牛顿法下的迭代次数：

回答问题：

1.

Theta1=-16.3787

Theta2=0.1483

Theta3=0.1589

由第二幅图可以看出，在第4次迭代后趋于完全收敛。

2.

根据得到的theta值来构建逻辑回归，计算第一次考试20分，第二次考试80分不被录取的概率为0.668

1.根据本次和之前的实验，对梯度下降和牛顿法的优缺点作个总结：

牛顿法：是通过求解目标函数的一阶导数为0时的参数，进而求出目标函数最小值时的参数。

优点：收敛速度很快，而且不需要知道学习率。

海森矩阵的逆在迭代过程中不断减小，可以起到逐步减小步长的效果。

缺点：海森矩阵的逆计算复杂，代价比较大，因此有了拟牛顿法。

梯度下降法：是通过梯度方向和步长，直接求解目标函数的最小值时的参数。

越接近最优值时，步长应该不断减小，否则会在最优值附近来回震荡。

优点：计算简单，实现容易。

缺点：收敛速度比较慢，数据量大还会导致内存不足。

1.导入数据

x=load('ex4x.dat');

y=load('ex4y.dat');

m=length(y);

x=[ones(m,1),x];

n=size(x,2);

2.绘制数据图

pos=find(y==1);

neg=find(y==0);

plot(x(pos,2),x(pos,3),'+');

hold on

plot(x(neg,2),x(neg,3),'o');

xlabel('exam1')

ylabel('exam2')

3.牛顿法

maxiter=100;

theta=zeros(size(x(1,:)))';

e=1e-6;

H=zeros(n,n);

g=inline('1.0./(1.0+exp(-z))');

for i=1:maxiter

z=x*theta;

h=g(z);

cost(i,1)=-(1/m)*sum(y.*log(h)+(1-y).*log(1-h));

dtheta=(1/m)*x'*(h-y);

H=(1/m).*x'*diag(h)*diag(1-h)*x;

if (i > 1) && (abs(cost(i,1) - cost(i-1,1)) <= e )

break;

end

theta=theta-H^(-1)*dtheta;

jilv(i,1)=cost(i,1);

end

4.绘制决策边界和代价函数

y_dec=(-theta(1,1).*x(:,1)-theta(2,1).*x(:,2))/theta(3,1);

plot(x(:,2),y_dec,'-');

figure

plot(1:i,cost,'-')

theta

p=1-g(theta(1,1)+theta(2,1)*20+theta(3,1)*80)