基于FPGA的数字图像处理- 图像分割【4.6】_fpga 画面分割

第10章 图像分割

10.1 图像分割简介

         图像分割是将图像划分成若干个互不相交的小区域的过程，所谓 小区域是某种意义下具有共同属性的像素的连通集合。 图像分割可以将图像中有意义的特征或者应用所需要的特征信息 提取出来，其最终结果是将图像分解成一些具有某种特征的单元，称 为图像的基元。相对于整幅图像来说，这种图像基元更容易被快速处 理。无论是图像处理、分析、理解与识别，其基础工作一般都建立在 图像分割的基础上。 在本章，我们将首先讨论几种常见的图像分割的方法，然后重点 讲述局部自适应分割算法及Canny算子在FPGA中的应用。

10.2 基于阈值的分割

        由于图像阈值的直观性和易于实现的性质，使它在图像分割应用 中处于中心地位。阈值分割方法实际上是输入图像f到输出图像g的变 换，如式（10-1）所示。

        其中，T为阈值，对于物体的图像元素g(i,j)=1，对于背景的图像 元素g(i,j)=0。 由此可见，阈值分割算法的关键是确定阈值。如果能确定一个合 适的阈值就可准确地将图像分割开来。阈值确定后，将阈值与像素点 的灰度值逐个进行比较，并且像素分割可对各像素并行地进行，分割 的结果直接给出图像区域。 阈值分割的优点是计算简单、运算效率较高、速度快，它在重视 运算效率的应用场合（如用于硬件实现）得到了广泛应用。 阈值分割技术又可分为全局阈值分割和局部自适应阈值分割。 10.2.1 全局阈值分割 全局阈值是指整幅图像使用同一个阈值进行分割处理，适用于背 景和前景有明显对比的图像。它是根据整幅图像确定的：T=T(f)。

        但 是这种方法只考虑像素本身的灰度值，一般不考虑空间特征，因而对 噪声很敏感。常用的全局阈值选取方法有利用图像灰度直方图的峰谷 法、最小误差法、最大类间方差法、最大熵自动阈值法及其他一些方 法。 下面以最大类间方差分割算法（OTSU）来说明全局分割阈值的应 用。最大类间方差法是由日本学者大津于1979年提出的，是一种自适 应的阈值确定的方法，又称为大津法，简称OTSU。它是按图像的灰度 特性，将图像分成背景和目标两部分。背景和目标之间的类间方差越 大，说明构成图像的两部分的差别越大，当部分目标错分为背景或部分背景错分为目标都会导致两部分差别变小。因此，使类间方差最大 的分割意味着错分概率最小。 对于图像I(x,y)，前景（目标）和背景的分割阈值记作T，属于前 景的像素点数占整幅图像的比例记为ω0 ，其平均灰度为μ0 ；背景 像素点数占整幅图像的比例为ω1 ，其平均灰度为μ1 。图像的总平 均灰度记为μ，类间方差记为g。假设图像的背景较暗，并且图像的大 小为M×N，图像中像素的灰度值小于阈值T的像素个数记作N0 ，若把 像素灰度大于阈值T的像素个数记作N1 ，则有

采用遍历的方法得到使类间方差最大的阈值T，即为所求值。 Otsu算法步骤如下： 设图像包含L个灰度级(0,1…,L-1)，灰度值为i的像素点数为Ni ，图像总的像素点数为N＝N0 +N1 +…+N(L-1)。灰度值为i的点的概率 为

OTSU的C示例代码如下：
void OTSU_Segment(BYTE * m_pBitmap,BYTE * p_Segment,DWORD
m_dwHeight,DWORD m_dwWidth,)
{
int i,j=0;
int k=0;
int fii=0;
double mk=0,pk=0;
unsigned long sigma2=0;
unsigned long sigmag=0;
int Hit[256];int max;
double p[256]; //每个像素的概率
double mg=0; //整幅图像的平均灰度
memset(Hit,0,256*sizeof(int)); //将分配的内存清零
if( !m_pBitmap)return; //如果没有打开图像则返回
for( i =0 ; i ＜ m_dwHeight; i++)
for( j = 0; j ＜ m_dwWidth; j++)
Hit[m_pBitmap[i*m_dwWidth+j]]++; //求得直方图
for (i=0;i＜256;i++)
p[i]=(double)Hit[i]/(m_dwHeight*m_dwWidth); // 直 方
图概率数组
for (i=0;i＜256;i++) mg+=i*p[i]; //图像平均灰度
for (i=0;i＜256;i++) sigmag+=(i-mg)*(i-mg)*p[i]; //整体
方差
max=0;
for (k=1;k＜256;k++) //从0到256遍历OTSU算法类间方差
{
pk=0;
mk=0;
for (i=0;i＜k;i++)
{
pk+=p[i];
mk+=i*p[i];
}
if (pk!=0)
sigma2=(mg*pk-mk)*(mg*pk-mk)/(pk*(1-pk));
if (sigma2>max){
max=sigma2;
fii=k;
}
}
for( i =0 ; i ＜ m_dwHeight; i++)
{
for( j = 0; j ＜ m_dwWidth; j++)
{
if (m_pBitmap[i*m_dwWidth+j]>=fii)
p_Segment [i*m_dwWidth+j]=255;
else
p_Segment[i*m_dwWidth+j]=0;
}
}
}

10.2.2 局部自适应阈值分割

        全局阈值分割算法简单，对于双峰直方图图像有很好的分割效 果。然而全局阈值分割的缺点也是显而易见的：对于图像噪声和光照 不均匀性十分敏感，在这种情况下，采用全局阈值分割往往会失败。 图10-2是图像的OTSU分割结果。可见，由于边缘光照的不均匀性，造 成边缘分割失败。图像边缘光线较暗的地方被分割为0，中间较亮的地 方分割成功。

如何规避光线不均匀带来的影响？一种典型的处理办法就是采用 局部自适应阈值分割。 局部自适应阈值分割根据像素邻域块的像素值分布来确定该像素 位置上的二值化阈值。这样做的好处在于每个像素位置处的二值化阈 值不是固定不变的，而是由其周围邻域像素的分布来决定的。亮度较 高的图像区域的二值化阈值通常较高，而亮度较低的图像区域的二值化阈值则会相适应地变小。不同亮度、对比度、纹理的局部图像区域 将会拥有相对应的局部二值化阈值。 常用的局部自适应阈值是局部邻域块的均值和局部邻域块的高斯 加权和。 下面考虑对图10-2（a）所示的不均匀光照的笔记图像进行局部自 适应高斯分割。首先我们给出局部自适应高斯分割的定义。将处理窗 口设为矩形移动窗，设r为处理窗口的半径，T为窗口内的局部分割后 阈值，μ为窗口内像素均值，σ2 为窗口内像素方差，r为处理窗口半 径，I(x,y)为输入像素值，g(x,y)为分割后的像素值，K为一个大于0 的常数。有如下定义：

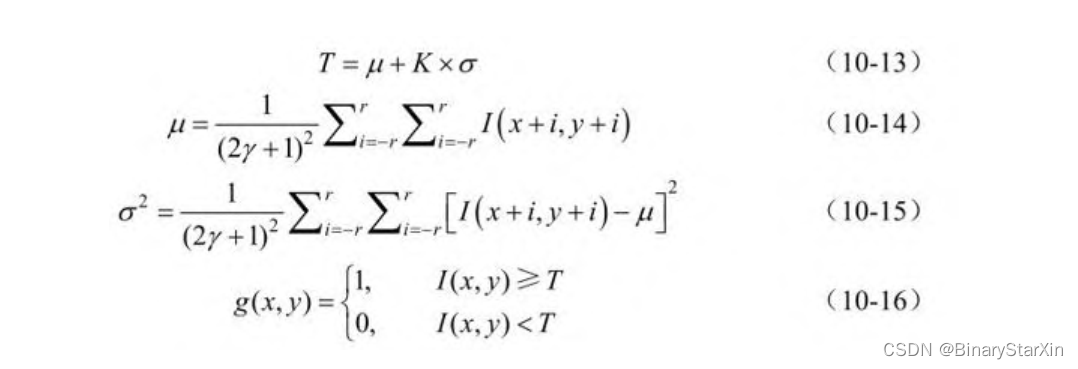
通常情况下，根据不同的图像，K为0～4的常数，这里我们将K取为1。窗口半径取为7。本算法的C代码实例如下：
 

/*高斯局部分割*/
#define GUAS_SEGMENT_RADIUS 7 /*处理半径*/
#define GUAS_SEGMENT_NUM_ALL ((2*GUAS_SEGMENT_RADIUS+1)*
(2*GUAS_
SEGMENT_RADIUS+1))
#define GUAS_SEGMENT_PARA 1 //分割系数void GausSegment(BYTE * m_pBitmap,BYTE * p_Segment,DWORD
m_dwHeight,DWORD m_dwWidth)
{
int i,j,m,k = 0;
if (!m_pBitmap)return; //打开图像非法则返回
memset(p_Segment,255,m_dwHeight*m_dwWidth);
double sum,average,temp1,temp2 = 0;
/*开窗*/
for (i = GUAS_SEGMENT_RADIUS;i＜ m_dwHeight -
GUAS_SEGMENT_RADIUS; i++)
for (j = GUAS_SEGMENT_RADIUS;j＜m_dwWidthGUAS_SEGMENT_RADIUS;j++)
{
sum = 0;
temp2 = 0;
/*首先计算窗口内均值*/
for (m = -GUAS_SEGMENT_RADIUS; m ＜=
GUAS_SEGMENT_RADIUS; m++)
for (k = -GUAS_SEGMENT_RADIUS; k ＜=
GUAS_SEGMENT_RADIUS; k++)
sum += m_pBitmap[(i + m)*m_dwWidth + j +
k];//求窗口像素总和
average = sum / GUAS_SEGMENT_NUM_ALL;/*求窗口像素
均值*/
temp1 = GUAS_SEGMENT_NUM_ALL*(average -
m_pBitmap[i*m_dwWidth+ j])* (average -
m_pBitmap[i*m_dwWidth + j]);for (m = -GUAS_SEGMENT_RADIUS; m ＜=
GUAS_SEGMENT_RADIUS; m++)
for (k = -GUAS_SEGMENT_RADIUS; k ＜=
GUAS_SEGMENT_RADIUS; k++)
temp2 +=GUAS_SEGMENT_PARA*GUAS_SEGMENT_PARA*
(m_pBitmap[(i + m)*m_dwWidth + j + k]- average)*
(m_pBitmap[(i + m)*m_dwWidth + j + k]- average);
if (temp1 > temp2)
p_Segment [i*m_dwWidth + j]= 0;
else p_Segment [i*m_dwWidth + j]= 255;
}
}

        可见，局部分割由于是在局部内求取分割门限，选取适合的窗口 尺寸可以保证窗口内像素直方图有明显的分割门限，可以很好地达到预期的分割效果。因此，局部分割有效地消除了光照不均匀带来的影 响。

10.3 基于边缘的分割

        所谓边缘是指图像中两个不同区域的边界线上连续的像素点的集 合，是图像局部特征不连续性的反映，体现了灰度、颜色、纹理等图 像特性的突变。通常情况下，基于边缘的分割方法指的是基于灰度值 的边缘检测，它是建立在边缘灰度值会呈现出阶跃型或屋顶型变化这 一观测基础上的方法。 阶跃型边缘两边像素点的灰度值存在着明显的差异，而屋顶型边 缘则位于灰度值上升或下降的转折处。正是基于这一特性，可以使用 微分算子进行边缘检测，即使用一阶导数的极值与二阶导数的过零点 来确定边缘，具体实现时可以使用图像与模板进行卷积来完成。 常用的边缘检测方法有Sobel算子、Canny算子及霍夫变换等。我 们在本书中将详细介绍Canny算子的原理及FPGA实现。

10.3.1 Canny算子

        Canny算子在图像处理领域可谓大名鼎鼎，该算子是一个典型的边 缘检测算子，是由John F.Canny于1986年开发出来的一个多级边缘检 测算法。当然也有很多改进算法和变种。虽然推出的年代较早，但是 Canny算子依然被推崇为目前最优的边缘检测算子。 Canny的目标是找到一个最优的边缘检测算法，最优边缘检测的含 义如下。（1）最优检测：算法能够尽可能多地标识出图像中的实际边缘， 漏检真实边缘的概率和误检非边缘的概率都尽可能小。 （2）最优定位准则：检测到的边缘点的位置距离实际边缘点的位 置最近，或者是由于噪声影响引起检测出的边缘偏离物体的真实边缘 的程度最小； （3）检测点与边缘点一一对应：算子检测的边缘点与实际边缘点 应该是一一对应。 为 了 满 足 这 些 要 求 Canny 使 用 了 变 分 法 （ Calculus of Variations），这是一种寻找优化特定功能的函数的方法。最优检测 使用四个指数函数项表示，但是它非常近似于高斯函数的一阶导数。

10.3.2 Canny算子的计算步骤

        Canny边缘检测算法可以分为以下4个步骤。 1.图像平滑 求边缘主要是求图像的一阶或二阶导数，导数计算对图像噪声非 常敏感。因此，在进一步处理前，必须对图像进行平滑处理。 常用的平滑处理方法有均值滤波、双边滤波、高斯滤波和中值滤 波等。这里采用高斯滤波方式进行平滑处理。 在7.1.2节中，已经详细介绍了高斯滤波的原理，这里我们直接采 用尺寸为5×5和标准差为1.4的高斯核，具体如下：

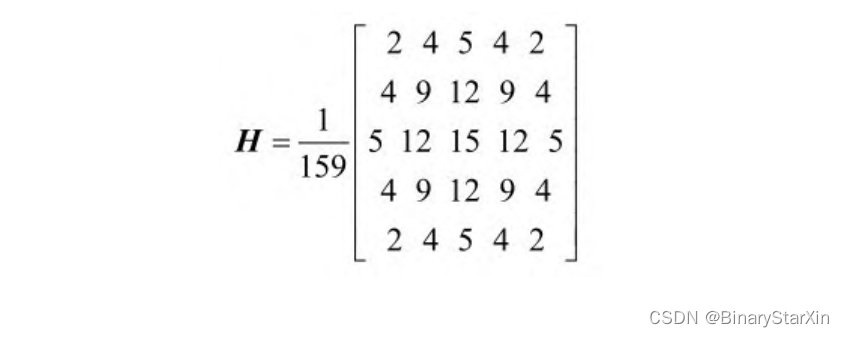
示例C++代码如下：
//输入图像存放在m_pBitmap
int i,j,m,k = 0;
int Gaus_Kernel[5][5]=
{
{2,4,5,4,2,},
{4,9,12,9,4},
{5,12,15,12,5},
{4,9,12,9,4},
{2,4,5,4,2}
};
BYTE *p_GausResult = new BYTE[m_dwHeight*m_dwWidth]; /*高
斯滤波结果*/
memset(p_GausResult,255,m_dwHeight*m_dwWidth);
/*首先进行5*5高斯滤波*/
double Gaus_Result = 0;
for (i = 2; i＜m_dwHeight - 2; i++)
for (j = 2; j＜m_dwWidth - 2; j++)
{
Gaus_Result = 0;
for (m = -2; m ＜= 2; m++)
for (k = -2; k ＜= 2; k++)
{
Gaus_Result += Gaus_Kernel[m+2][k+2]*(m_pBitmap[(i
+ m)*m_dwWidth+j+
k]/159.0);
}p_GausResult[i*m_dwWidth + j]= (BYTE)Gaus_Result ;
}

图10-4展示了高斯滤波的结果（左侧为测试原图像）。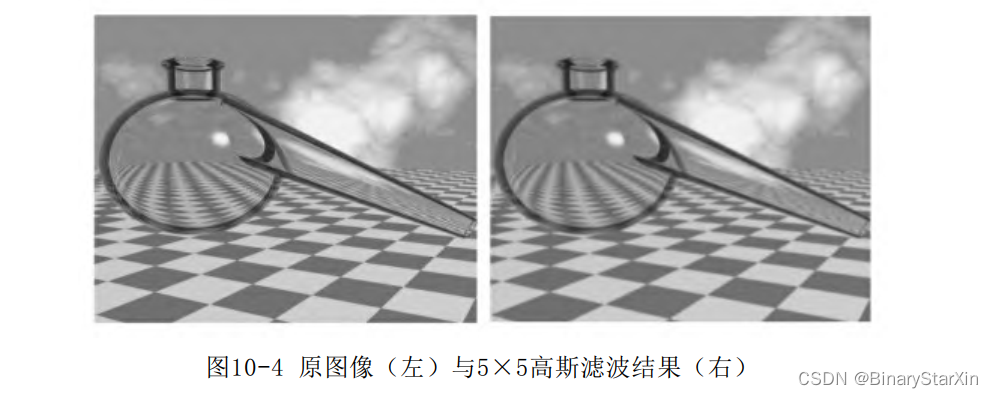

可以看到，图像明显得到了一定程度的平滑。