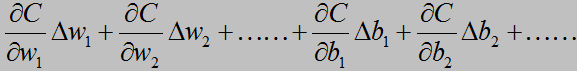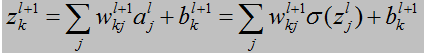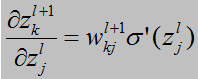- 1Stable Diffusion 使用详解(4)---- 制作情景文本_stablediffusion 文本生成文本
- 2Armbian安装1panel教程
- 3Python详解02_Python介绍、变量、输入输出语句
- 4【算法系列】双指针
- 5Git完整基础教程、浅显易懂(附全部命令执行方法)_git入门教程 简单易懂
- 651单片机dds信号发生器 扫频 c语言,基于DDS正弦信号发生器设计.doc
- 7网络安全期末复习_山东大学网络安全复习csdn
- 823-480、基于Arduino Uno驱动的面部识别跟踪相机设计-CSDN_arduino uno 图像识别
- 9STM32学习·HAL库·STM32CubeMX系列学习(安装和使用)_stm32cubemx怎么添加hal库
- 10Kafka高性能核心——pageCache与zeroCopy_零拷贝和页缓存的区别
反向传播算法的直观理解
赞
踩
一、反向传播的由来
在我们开始DL的研究之前,需要把ANN—人工神经元网络以及bp算法做一个简单解释。关于ANN的结构,我不再多说,网上有大量的学习资料,主要就是搞清一些名词:
输入层/输入神经元,输出层/输出神经元,隐层/隐层神经元,权值,偏置,激活函数
接下来我们需要知道ANN是怎么训练的,假设ANN网络已经搭建好了,在所有应用问题中(不管是网络结构,训练手段如何变化)我们的目标是不会变的,那就是网络的权值和偏置最终都变成一个最好的值,这个值可以让我们由输入可以得到理想的输出,于是问题就变成了y=f(x,w,b)(x是输入,w是权值,b为偏置,所有这些量都可以有多个,比如多个x1,x2,x3……最后f()就好比我们的网络它一定可以用一个函数来表示,我们不需要知道f(x)具体是怎样的函数,从小我们就认为只要是函数就一定要是可表示的,像f(x)=sin(x)一样,但是请摈弃这样的错误观念,我们只需要知道一系列的w和b决定了一个函数f(x),这个函数让我们由输入可以计算出合理的y)
最后的目标就变成了尝试不同的w,b值,使得最后的y=f(x)无限接近我们希望得到的值t
但是这个问题依然很复杂,我们把它简化一下,让(y-t)^2的值尽可能的小。于是原先的问题化为了C(w,b)=(f(x,w,b)-t)^2取到一个尽可能小的值。这个问题不是一个困难的问题,不论函数如何复杂,如果C降低到了一个无法再降低的值,那么就取到了最小值(假设我们不考虑局部最小的情况)
如何下降?数学告诉我们对于一个多变量的函数f(a,b,c,d,……)而言,我们可以求得一个向量,它称作该函数的梯度,要注意的是,梯度是一个方向向量,它表示这个函数在该点变化率最大的方向(这个定理不详细解释了,可以在高等数学教材上找到)于是C(w,b)的变化量ΔC就可以表示成
其中
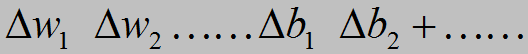
事实上,梯度下降的思想就是这样考虑的,我们使得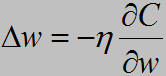
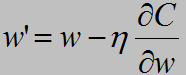
ok,到这里,似乎所有的问题都解决了,让我们重新整理一下思绪,我们将问题转化了很多步:
网络权值偏置更新问题 ==> f(x,w,b)的结果逼近t ==> C(w,b)=(f(x,w,b)-t)^2取极小值问题 ==> C(w,b)按梯度下降问题 ==>取到极小值,网络达到最优
千万别忘了一点!!推导基于一个前提:我们已经提前知道了当前点的梯度。然而事实并非如此!!
这个问题困扰了NN研究者多年,1969年M.Minsky和S.Papert所著的《感知机》一书出版,它对单层神经网络进行了深入分析,并且从数学上证明了这种网络功能有限,甚至不能解决象"异或"这样的简单逻辑运算问题。同时,他们还发现有许多模式是不能用单层网络训练的,而对于多层网络则没有行之有效的低复杂度算法,最后他们甚至认为神经元网络无法处理非线性问题。然而于1974年,Paul Werbos首次给出了如何训练一般网络的学习算法—back propagation。这个算法可以高效的计算每一次迭代过程中的梯度,让以上我们的推导得以实现!!
不巧的是,在当时整个人工神经网络社群中无人知晓Paul所提出的学习算法。直到80年代中期,BP算法才重新被David Rumelhart、Geoffrey Hinton及Ronald Williams、David Parker和Yann LeCun独立发现,并获得了广泛的注意,引起了人工神经网络领域研究的第二次热潮。
二、原理的引入
上面已经提到,所谓反向传播,就是计算梯度的方法。对于反向传播,先不急着介绍它的原理,很多文章直接引入公式,反而使得我们很难去理解。这里先引入知乎上某位大神的回答。来源:知乎https://www.zhihu.com/question/27239198?rf=24827633
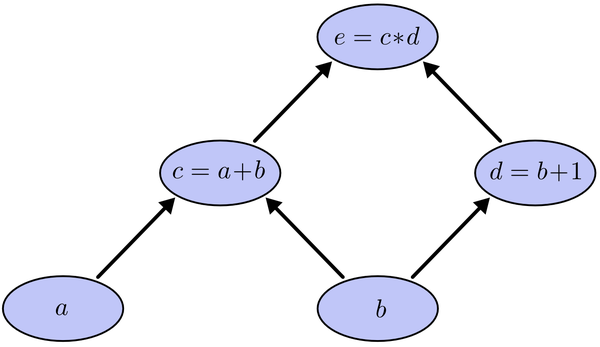
假设输入a=2,b=1,在这种情况下,我们很容易求出相邻节点之间的偏导关系
利用链式法则:
以及
的值等于从a到e的路径上的偏导值的乘积,而
的值等于从b到e的路径1(b-c-e)上的偏导值的乘积加上路径2(b-d-e)上的偏导值的乘积。也就是说,对于上层节点p和下层节点q,要求得
,需要找到从q节点到p节点的所有路径,并且对每条路径,求得该路径上的所有偏导数之乘积,然后将所有路径的 “乘积” 累加起来才能得到
的值。
这种情况下偏导很容易求得,因为我们已经知道网络的函数关系式,e=(a+b)*(b+1),这是一个没有权值干预,已知输入与输出之间关系的网络。实际当中我们只是知道e与输出之间的关系,就是上面说的C=(y-t)^2,而且会有成千上万的权值和偏置干预求导的过程。那么换个思路,能不能求输出对结果的偏导呢?
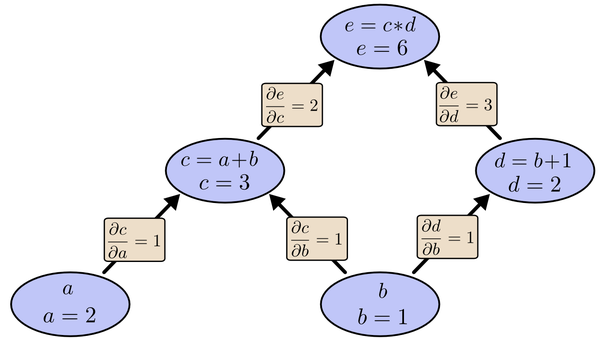
再利用上图的关系。节点c对e偏导2并将结果堆放起来,节点d对e偏导3并将结果堆放起来,至此第二层完毕,求出各节点总堆放量并继续向下一层发送。节点c向a发送2*1并对堆放起来,节点c向b发送2*1并堆放起来,节点d向b发送3*1并堆放起来,至此第三层完毕,节点a堆放起来的量为2,节点b堆放起来的量为2*1+3*1=5, 即顶点e对b的偏导数为5。简要的概括,就是从最上层的节点e开始,以层为单位进行处理。对于e的下一层的所有子节点,将1乘以e到某个节点路径上的偏导值,并将结果“堆放”在该子节点中。等e所在的层按照这样传播完毕后,第二层的每一个节点都“堆放"些值,然后我们针对每个节点,把它里面所有“堆放”的值求和,就得到了顶点e对该节点的偏导。然后将这些第二层的节点各自作为起始顶点,初始值设为顶点e对它们的偏导值,以"层"为单位重复上述传播过程,即可求出顶点e对每一层节点的偏导数。
三、一个很好的例子
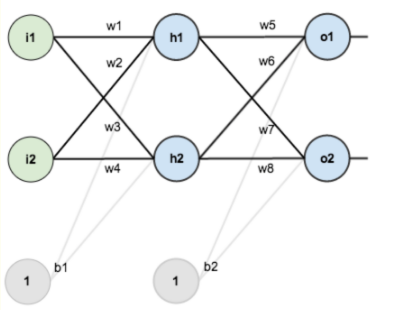
假设,你有这样一个网络层:
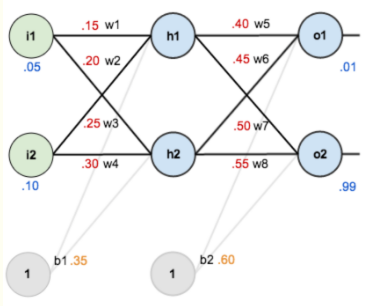
第一层是输入层,包含两个神经元i1,i2,和截距项b1;第二层是隐含层,包含两个神经元h1,h2和截距项b2,第三层是输出o1,o2,每条线上标的wi是层与层之间连接的权重,激活函数我们默认为sigmoid函数。
现在对他们赋上初值,如下图:
其中,输入数据 i1=0.05,i2=0.10;
输出数据 o1=0.01,o2=0.99;
初始权重 w1=0.15,w2=0.20,w3=0.25,w4=0.30;
w5=0.40,w6=0.45,w7=0.50,w8=0.88
目标:给出输入数据i1,i2(0.05和0.10),使输出尽可能与原始输出o1,o2(0.01和0.99)接近。
Step 1 前向传播
1.输入层---->隐含层:
计算神经元h1的输入加权和:

神经元h1的输出o1:(此处用到激活函数为sigmoid函数):

同理,可计算出神经元h2的输出o2:
![]()
2.隐含层---->输出层:
计算输出层神经元o1和o2的值:

![]()
这样前向传播的过程就结束了,我们得到输出值为[0.75136079 , 0.772928465],与实际值[0.01 , 0.99]相差还很远,现在我们对误差进行反向传播,更新权值,重新计算输出。
Step 2 反向传播
1.计算总误差
总误差:(square error)

但是有两个输出,所以分别计算o1和o2的误差,总误差为两者之和:


2.隐含层---->输出层的权值更新:
以权重参数w5为例,如果我们想知道w5对整体误差产生了多少影响,可以用整体误差对w5求偏导求出:(链式法则)
下面的图可以更直观的看清楚误差是怎样反向传播的:
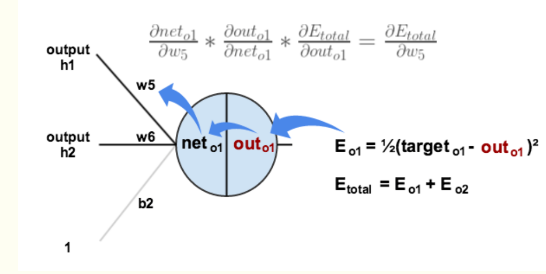
现在我们来分别计算每个式子的值:
计算![]() :
:

计算 :
:

(这一步实际上就是对sigmoid函数求导,比较简单,可以自己推导一下)
计算 :
:

最后三者相乘:

这样我们就计算出整体误差E(total)对w5的偏导值。
回过头来再看看上面的公式,我们发现:

为了表达方便,用![]() 来表示输出层的误差:
来表示输出层的误差:

因此,整体误差E(total)对w5的偏导公式可以写成:

如果输出层误差计为负的话,也可以写成:

最后我们来更新w5的值:

(其中,![]() 是学习速率,这里我们取0.5)
是学习速率,这里我们取0.5)
同理,可更新w6,w7,w8:

3.隐含层---->隐含层的权值更新:
方法其实与上面说的差不多,但是有个地方需要变一下,在上文计算总误差对w5的偏导时,是从out(o1)---->net(o1)---->w5,但是在隐含层之间的权值更新时,是out(h1)---->net(h1)---->w1,而out(h1)会接受E(o1)和E(o2)两个地方传来的误差,所以这个地方两个都要计算。

计算![]() :
:

先计算 :
:
![]()
![]()


同理,计算出:
![]()
两者相加得到总值:

再计算![]() :
:

再计算![]() :
:

最后,三者相乘:

为了简化公式,用sigma(h1)表示隐含层单元h1的误差:

最后,更新w1的权值:
![]()
同理,额可更新w2,w3,w4的权值:

这样误差反向传播法就完成了,最后我们再把更新的权值重新计算,不停地迭代,在这个例子中第一次迭代之后,总误差E(total)由0.298371109下降至0.291027924。迭代10000次后,总误差为0.000035085,输出为[0.015912196,0.984065734](原输入为[0.01,0.99]),证明效果还是不错的
四、最一般的情况
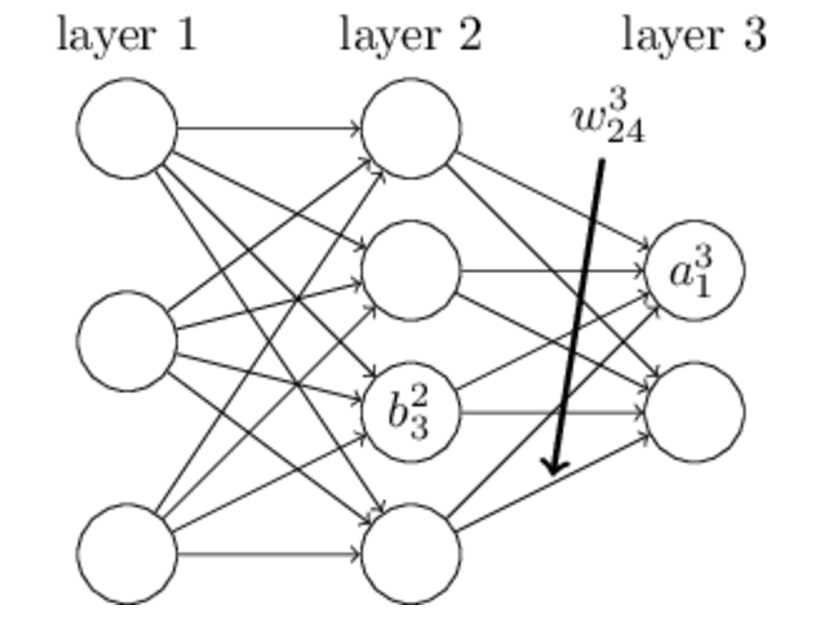
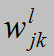 表示第l-1层的第
表示第l-1层的第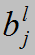 表示第
表示第 表示第
表示第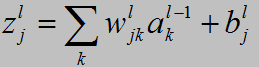
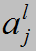 表示第l
表示第l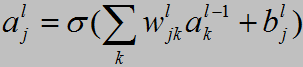
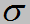 表示激活函数。
表示激活函数。
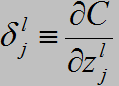

以上4个方程中,第一个方程其实不难理解,就是求输出对估价函数C的偏导。
唯一比较困难的,就是第二个方程,它给出了根据下一层的错误量δl+1计算δl的等式。为证明该等式,我们先依据δkl+1=∂C/∂zkl+1重新表达下等式δlj =∂C/∂zlj。这里可以应用链式法则:
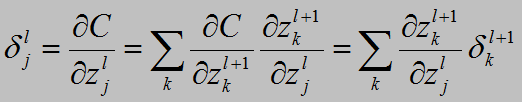
在最后一行,我们互换了下表达式右侧的两项,并取代了 δkl+1的定义。为了对最后一行的第一项求值,注意:
作微分,我们得到
代回 (42) 我们得到
这就是以分量形式呈现的 (BP2)。后两式在完成了BP2证明之后就不太难了,留给读者来证明。