C语言例程：插入排序_要求根据指定接口,使用直接插入排序算法实现一组数从小到大排序,要求输出每一趟的

插入排序

实例说明

将一个整数数组按从小到大的顺序进行排序，主要学习基本的插入排序和改进的冒泡排序的
算法和应用。

实例解析

排序（sort）

所谓排序，就是要整理文件中的记录，使之按关键字递增（或递减）次序排列起来，其确切
定义如下。
输入：n 个记录 R1，R2，…，Rn，其相应的关键字分别为 K1，K2，…，Kn。
输出：Ril，Ri2，…，Rin，使得 Ki1≤Ki2≤…≤Kin。（或 Ki1≥Ki2≥…≥Kin）。
被排序对象：文件，由一组记录组成。记录则由若干个数据项（或域）组成。其中有一项可
用来标识一个记录，称为关键字项。该数据项的值称为关键字（Key）。在不易产生混淆时，将关
键字项简称为关键字。
用来作为排序运算依据的关键字，可以是数字类型，也可以是字符类型。关键字的选取应根
据问题的要求而定。例如，在高考成绩统计中将每个考生作为一个记录。每条记录包含准考证号、
姓名、各科的分数和总分数等项内容。若要惟一地标识一个考生的记录，则必须用“准考证号”
作为关键字。若要按照考生的总分数排名次，则需用“总分数”作为关键字。

排序的稳定性

当待排序记录的关键字均不相同时，排序结果是惟一的，否则排序结果不惟一。
在待排序的文件中，若存在多个关键字相同的记录，经过排序后，这些具有相同关键字记录
之间的相对次序保持不变，该排序方法是稳定的；若具有相同关键字的记录之间的相对次序发生
变化，则称这种排序方法是不稳定的。
注意：排序算法的稳定性是针对所有输入实例而言的。即在所有可能的输入实例中，只要有
一个实例使得算法不满足稳定性要求，则该排序算法就是不稳定的。

排序方法的分类

（1）按是否涉及数据的内/外存交换分
在排序过程中，若整个文件都是放在内存中处理，排序时不涉及数据的内/外存交换，则称之
为内部排序（简称内排序）；反之，若排序过程中要进行数据的内、外存交换，则称之为外部排序。
注意：① 内排序适用于记录个数不很多的小文件。② 外排序则适用于记录个数较多，不能
一次将全部记录放入内存的大文件。
（2）按策略划分内部排序方法
可以分为 5 类：插入排序、选择排序、交换排序、归并排序和分配排序。

待排序文件的常用存储方式

（1）以顺序表（或直接用向量）作为存储结构，其排序过程为对记录本身进行物理重排（即
通过关键字之间的比较判定，将记录移到合适的位置）。
（2）以链表作为存储结构，其排序过程无需移动记录，仅需修改指针。通常将这类排序称为
链表（或链式）排序。
（3）用顺序的方式存储待排序的记录，但同时建立一个辅助表（如包括关键字和指向记录
位置的指针组成的索引表）。其排序过程为只需对辅助表的表目进行物理重排（即只移动辅助表
的表目，而不移动记录本身）。此方法适用于难于在链表上实现，且需避免排序过程中移动记录
的排序方法

待排序文件的顺序存储结构表示

 #define n l00 /* 假设的文件长度，即待排序的记录数目 */ 
 typedef int KeyType; /* 假设的关键字类型 */ 
 typedef struct{ /* 记录类型 */ 
 KeyType key; /* 关键字项 */ 
 InfoType otherinfo;/* 其他数据项，类型 InfoType 依赖于具体应用而定义 */ 
 }RecType; 
 typedef RecType SeqList[n+1];/* SeqList 为顺序表类型，表中第 0 个单元一般用作哨兵 */
1
2
3
4
5
6
7

若关键字类型没有比较算符，则可事先定义宏或函数来表示比较运算。例如，关键字为字符
串时，可定义宏“#define LT(a,b)(Stromp((a),(b))<0)”。那么算法中“a<b”可用“LT(a,b)”取代。

排序算法性能评价

（1）评价排序算法好坏的标准
评价排序算法好坏的标准主要有两条：执行时间和所需的辅助空间；算法本身的复杂程度。
（2）排序算法的空间复杂度
若排序算法所需的辅助空间并不依赖于问题的规模 n，即辅助空间是 O（1），则称之为就地
排序（In-PlaceSou）。非就地排序一般要求的辅助空间为 O（n）。
（3）排序算法的时间开销
大多数排序算法的时间开销主要是关键字之间的比较和记录的移动。有些排序算法的执行时
间不仅依赖于问题的规模，还取决于输入实例中数据的状态。

插入排序

插入排序（Insertion Sort）的基本思想是：每次将一个待排序的记录按其关键字大小插入到前
面已经排好序的子文件中的适当位置，直到全部记录插入完成为止
有两种插入排序方法：直接插入排序和希尔排序。

直接插入排序

（1）基本思想
假设待排序的记录存放在数组 R[1…n]中。初始时，R[1]自成一个有序区，无序区为 R[2…n]。
从 i=2 起直至 i=n 为止，依次将 R[i]插入当前的有序区 R[1…i−1]中，生成含 n 个记录的有序区。
（2）第 i−1 趟直接插入排序
通常将一个记录 Ri插入到当前的有序区，使得插入后仍保证该区间里的记录
是按关键字有序的操作，称为第 i-1 趟直接插入排序。
排序过程的某一中间时刻，R 被划分成两个子区间 R[1…i−1]（已排好序的有序区）和 R[i…n]
（当前未排序的部分，可称无序区）。
直接插入排序的基本操作是将当前无序区的第 1 个记录 R[i]插入到有序区 R[1…i−1]中适当的
位置上，使 R[1…i]变为新的有序区。因为这种方法每次使有序区增加 1 个记录，通常称增量法。
插入排序与打扑克时整理手上的牌非常类似。摸来的第 1 张牌无需整理，此后每次从桌上的
牌（无序区）中摸最上面的 1 张并插入左手的牌（有序区）中正确的位置上。为了找到这个正确
的位置，需自左向右（或自右向左）将摸来的牌与左手中已有的牌逐一比较。

一趟直接插入排序

（1）简单方法
首先在当前有序区 R[1…i−1]中查找 R[i]的正确插入位置 k(1≤k≤i−1)；然后将 R[k…i−1]中的记
录均后移一个位置，腾出 k 位置上的空间插入 R[i]。
注意：若 R[i]的关键字大于等于 R[1．．i−1]中所有记录的关键字，则 R[i]就插入原位置。
（2）改进的方法
这是一种查找比较操作和记录移动操作交替进行的方法。
具体做法：将待插入记录 R[i]的关键字从右向左依次与有序区中记录 Rj的关
键字进行比较：①若 R[j]的关键字大于 R[i]的关键字，则将 R[j]后移一个位置；②若 R[j]的关键字
小于或等于 R[i]的关键字，则查找过程结束，j+1 即为 R[i]的插入位置。
关键字比 R[i]的关键字大的记录均已后移，所以 j+1 的位置已经腾空，只要将 R[i]直接插入
此位置即可完成一趟直接插入排序。

直接插入排序算法

算法描述如下：

 void lnsertSort(SeqList R) 
 { //对顺序表 R 中的记录 R[1..n]按递增序进行插入排序
 int i，j；
 for(i=2;i<=n；i++) //依次插入 R[2]，…，R[n] 
 if(R[i].key<R[i-1].key){//若 R[i].key 大于等于有序区中所有的 keys，则 R[i]应在原有位置上
 R[0]=R[i];j=i-1; //R[0]是哨兵，且是 R[i]的副本
 do{ //从右向左在有序区 R[1．．i-1]中查找 R[i]的插入位置
 R[j+1]=R[j]； //将关键字大于 R[i].key 的记录后移
 j-- ；
 }while(R[0].key<R[j].key)； //当 R[i].key≥R[j].key 时终止
 R[j+1]=R[0]； //R[i]插入到正确的位置上
 }//endif 
 }//InsertSort
1
2
3
4
5
6
7
8
9
10
11
12
13

程序代码

#include <stdio.h> 
#define MAX 255 
int R[MAX]; 
void Insert_Sort(int n) 
{ /* 对数组 R 中的记录 R[1..n]按递增序进行插入排序 */ 
	int i,j; 
	for(i=2;i<=n;i++) /* 依次插入 R[2]，…，R[n] */ 
		if(R[i]<R[i-1]) 
		{/* 若 R[i]大于等于有序区中所有的 R，则 R[i] 应在原有位置上 */ 
			R[0]=R[i];j=i-1; /* R[0]是哨兵，且是 R[i]的副本 */ 
			do{ /* 从右向左在有序区 R[1．．i-1]中查找 R[i]的插入位置 */ 
				R[j+1]=R[j]; /* 将关键字大于 R[i]的记录后移 */ 
				j--; 
			}while(R[0]<R[j]); /* 当 R[i]≥R[j]时终止 */ 
		R[j+1]=R[0]; /* R[i]插入到正确的位置上 */ 
		} 
} 
main() 
{ 
	int i,n; 
	clrscr(); 
	puts("Please input total element number of the sequence:"); 
	scanf("%d",&n); 
	if(n<=0||n>MAX) 
	{ 
		printf("n must more than 0 and less than %d.\n",MAX); 
		exit(0); 
	} 
	puts("Please input the elements one by one:"); 
	for(i=1;i<=n;i++) 
		scanf("%d",&R[i]); 
	puts("The sequence you input is:"); 
	for(i=1;i<=n;i++) 
		printf("%4d",R[i]); 
	Insert_Sort(n); 
	puts("\nThe sequence after insert_sort is:"); 
	for(i=1;i<=n;i++) 
		printf("%4d",R[i]); 
	puts("\n Press any key to quit..."); 
	getch(); 
 
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

程序执行结果

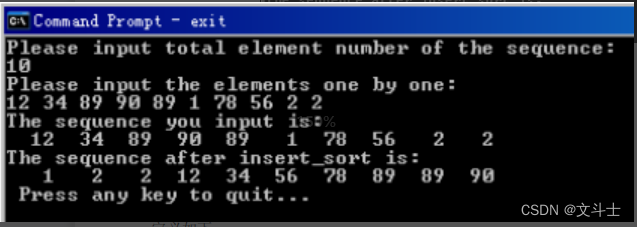
归纳注释

哨兵的作用：算法中引进的附加记录 R[0]称监视哨或哨兵（Sentinel）。哨兵有两个作用：① 进
行查找（插入位置）循环之前，它保存了 R[i]的副本，使不致于因记录后移而丢失 R[i]的内容；
② 它的主要作用是在查找循环中“监视”下标变量 j 是否越界。一旦越界（即 j=0），因为 R[0].key
和自己比较，循环判定条件不成立使得查找循环结束，从而避免了在该循环内的每一次均要检测
j 是否越界（即省略了循环判定条件“j>=1”）。
实际上，一切为简化边界条件而引入的附加结点（元素）均可称为哨兵。例如单链表中的头结
点实际上是一个哨兵。引入哨兵后可以使得测试查找循环条件的时间减少了一半，所以对于记录数
较大的文件节约的时间就相当可观。对于类似于排序这样使用频率非常高的算法，要尽可能地减少
其运行时间。所以不能把上述算法中的哨兵视为雕虫小技，而应该深刻理解并掌握这种技巧。
插入算法的时间性能分析：对于具有 n 个记录的文件，要进行 n-1 趟排序。各种状态下的时
间复杂度：初始文件状态为正序、反序和无序（平均）时，时间复杂度分别为 O(n)、O(n2
)和 O(n2
)。
算法的空间复杂度分析：算法所需的辅助空间是一个监视哨，辅助空间复杂度 S(n)=O(1)，是
一个就地排序。
直接插入排序的稳定性：直接插入排序是稳定的排序方法。