【机器学习】在Python中进行K-Means聚类和层次聚类_python中kmeans聚类

Python中聚类算法API的使用指南

聚类分析是数据分析中一种常见的无监督学习方法，通过将相似的对象分组在一起，我们能够识别出数据集中的自然分群。本文将介绍如何使用Python中的聚类算法接口，KMeans和层次聚类方法。

本文聚类示例的中药数据链接

K-Means 聚类

K-Means是一种广泛使用的聚类算法，它的目标是将数据点分成K个组，使得组内的点彼此相似，而组间的点不相似。在本文中K值为3，代码中表现为n_clusters=3。下面是如何使用K-Means聚类分析的步骤：

步骤一：导入必要的库

首先，需要导入KMeans类，它在sklearn.cluster模块中。

from sklearn.cluster import KMeans
1

步骤二：加载数据

我们使用pandas库来加载数据。确保数据文件的路径是正确的。

CLUS_FILE_PATH是你的数据路径，请替换。

import pandas as pd

df = pd.read_excel(CLUS_FILE_PATH, index_col=0)
1
2
3

步骤三：应用K-Means聚类

创建一个KMeans实例，并通过.fit()方法应用于数据。

kmeans = KMeans(n_clusters=3, random_state=0).fit(df)
1

步骤四：保存聚类结果

将聚类标签添加到原始数据框中，并保存到Excel文件。

df['Cluster'] = kmeans.labels_
df.to_excel('kmeans聚类分析结果.xlsx')
1
2

层次聚类

层次聚类是另一种常见的聚类方法，它通过构建一个多层次的嵌套分群树来组织数据，这个树被称为树状图（Dendrogram）。相对于K-Means，层次聚类不需要指定k值就可以完成聚类，但是要分类出标签的话，我们需要指定一个最大距离，如果两个样本超出这个最大距离则不属于同一类。

步骤一：导入库

导入进行层次聚类和绘制树状图所需的库。

from scipy.cluster.hierarchy import dendrogram, linkage, fcluster
from scipy.spatial.distance import pdist
1
2

步骤二：加载数据并计算距离矩阵

同样地，我们先加载数据，然后计算距离矩阵，使用欧式距离。

df = pd.read_excel(CLUS_FILE_PATH, index_col=0)
distance_matrix = pdist(df, metric='euclidean')
1
2

步骤三：执行层次聚类

使用linkage函数进行层次聚类，这里采用了’ward’方法。

Z = linkage(distance_matrix, method='ward')
1

步骤四：确定聚类数并保存结果

通过选择一个最大距离阈值来确定聚类数，并把聚类结果保存到Excel。

clusters = fcluster(Z, max_d=50, criterion='distance')
df['Cluster'] = clusters
df.to_excel('层次聚类分析结果.xlsx')
1
2
3

步骤五：绘制树状图并保存

最后，利用dendrogram函数绘制树状图，并保存为图片。

plt.figure(figsize=(10, 50))
dendrogram(Z, orientation='left', labels=df.index, leaf_rotation=0, leaf_font_size=10)
plt.title('层次聚类的树状图')
plt.ylabel('中药名称')
plt.xlabel('距离')
plt.tight_layout()
plt.savefig('层次聚类树状图.png')
plt.show()
1
2
3
4
5
6
7
8

层次聚类的树状图

我们可以看到，各个中药被层次聚类组织成了一颗一颗嵌套的树，这些树描述了不同中药之间的距离关系。

上面的步骤展示了如何使用Python进行K-Means聚类和层次聚类分析。聚类是一个强大的工具，可以帮助我们发现数据中的模式和结构。通过实践这些步骤，你会对聚类分析有更深的了解。

利用PCA降维以可视化聚类结果

绘图函数（可直接复制，然后按下文调用）

def plot_clus_2D(clustered_data, class_col, method):
    n_clusters = clustered_data[class_col].nunique()

    # 执行PCA降维，降至2维
    pca = PCA(n_components=2)
    data_reduced = pca.fit_transform(clustered_data.drop(columns=[class_col]))
    # 创建一个新的DataFrame来保存降维后的数据和聚类标签
    data_2D = pd.DataFrame(data_reduced, columns=['PC1', 'PC2'])
    data_2D[class_col] = clustered_data[class_col].values

    # 设置绘图参数
    fig, ax = plt.subplots(figsize=(10, 8))

    # 为每个聚类设置不同的颜色
    colors = ['red', 'green', 'blue']  # 你可以根据需要的聚类数修改颜色

    if n_clusters > 3:  # 如果聚类数超过3，扩展颜色列表
        import matplotlib.colors as mcolors
        colors = list(mcolors.TABLEAU_COLORS.values())[:n_clusters]

    # 绘制每个聚类的散点图
    for i in range(n_clusters):
        # 从聚类数据中提取当前聚类的数据
        cluster_data = data_2D[data_2D[class_col] == i]

        # 绘制散点图
        ax.scatter(cluster_data['PC1'], cluster_data['PC2'],
                   color=colors[i], label=f'Cluster {i}', alpha=0.5)

    # 添加图例和标题
    ax.legend()
    ax.set_title(f'{method} 聚类结果 - PCA降维可视化（2D）')
    ax.set_xlabel('Principal Component 1')
    ax.set_ylabel('Principal Component 2')

    # 显示图表
    save_path = os.path.join(IMAGE_FOLDER, f'{method} 聚类结果 - PCA降维可视化（2D）.png')
    plt.savefig(save_path)

    plt.show()


def plot_clus_3D(clustered_data, class_col, method):
    """

    :param clustered_data: 带有聚类结果标签的数据集
    :param class_col: 代表聚类结果的列名
    :param n_clusters: 有多少个
    :param method:
    :return:
    """

    n_clusters = clustered_data[class_col].nunique()

    # 执行PCA降维，降至3维
    pca = PCA(n_components=3)
    data_reduced = pca.fit_transform(clustered_data.drop(columns=[class_col]))
    # 创建一个新的DataFrame来保存降维后的数据和聚类标签
    data_3D = pd.DataFrame(data_reduced, columns=['PC1', 'PC2', 'PC3'])
    data_3D[class_col] = clustered_data[class_col].values

    # 设置绘图参数
    fig = plt.figure(figsize=(10, 8))
    ax = fig.add_subplot(111, projection='3d')

    # 为每个聚类设置不同的颜色
    colors = ['red', 'green', 'blue']  # 根据需要的聚类数修改颜色
    if n_clusters > 3:  # 如果聚类数超过3，扩展颜色列表
        import matplotlib.colors as mcolors
        colors = list(mcolors.TABLEAU_COLORS.values())[:n_clusters]

    # 绘制每个聚类的散点图
    for i in range(n_clusters):
        # 从聚类数据中提取当前聚类的数据
        cluster_data = data_3D[data_3D[class_col] == i]

        # 绘制散点图
        ax.scatter(cluster_data['PC1'], cluster_data['PC2'], cluster_data['PC3'],
                   color=colors[i], label=f'Cluster {i}', alpha=0.5)

    # 添加图例和标题
    ax.legend()
    ax.set_title(f'{method} 聚类结果 - PCA降维可视化（3D）')
    ax.set_xlabel('Principal Component 1')
    ax.set_ylabel('Principal Component 2')
    ax.set_zlabel('Principal Component 3')

    # 显示图表
    save_path = os.path.join(IMAGE_FOLDER, f'{method}_聚类结果_PCA降维可视化（3D）.png')
    plt.savefig(save_path)
    plt.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92

示例调用

clus_data = pd.read_excel('kmeans聚类分析结果.xlsx', index_col=0)
plot_clus_2D(clustered_data=clus_data, class_col='Cluster', method='K-means')
plot_clus_3D(clustered_data=clus_data, class_col='Cluster', method='K-means')

clus_data = pd.read_excel('层次聚类分析结果.xlsx', index_col=0)
plot_clus_2D(clustered_data=clus_data, class_col='Cluster', method='层次聚类')
plot_clus_3D(clustered_data=clus_data, class_col='Cluster', method='层次聚类')

1
2
3
4
5
6
7
8

2D可视化

K-Means聚类结果

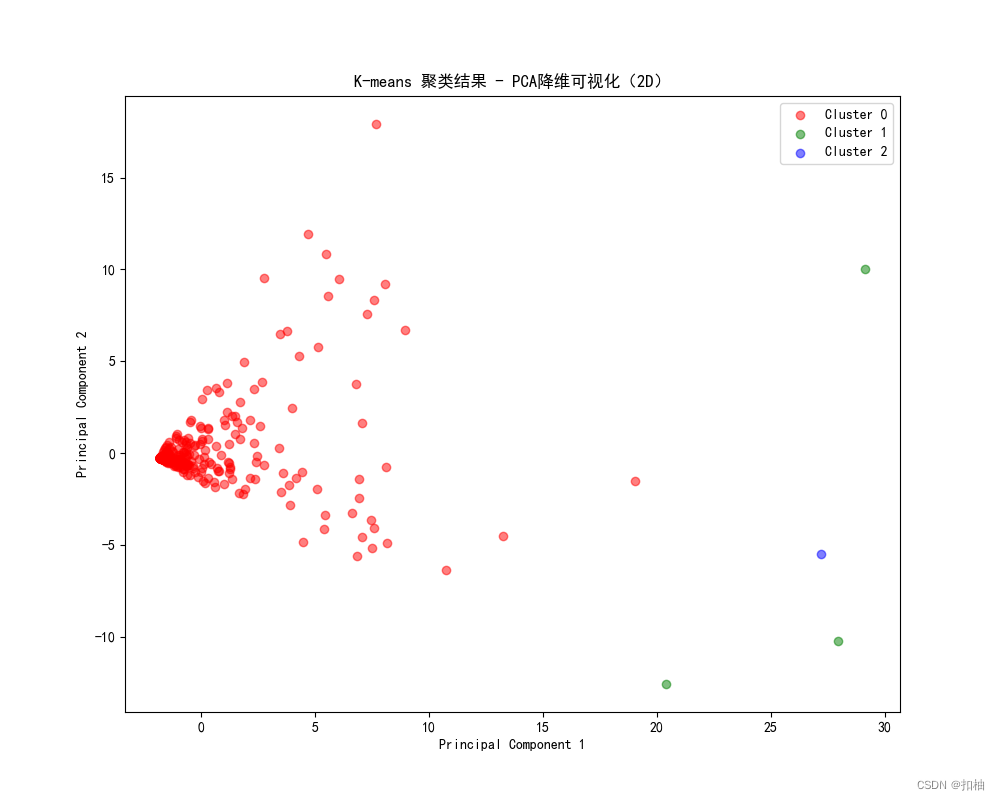
层次聚类结果

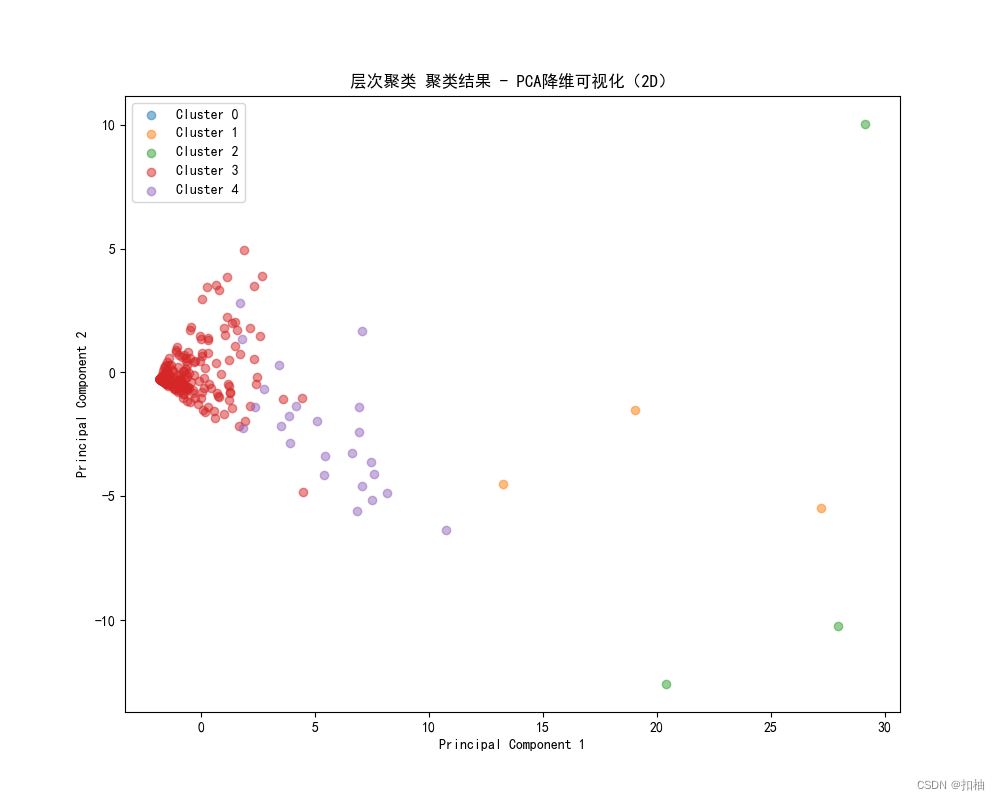
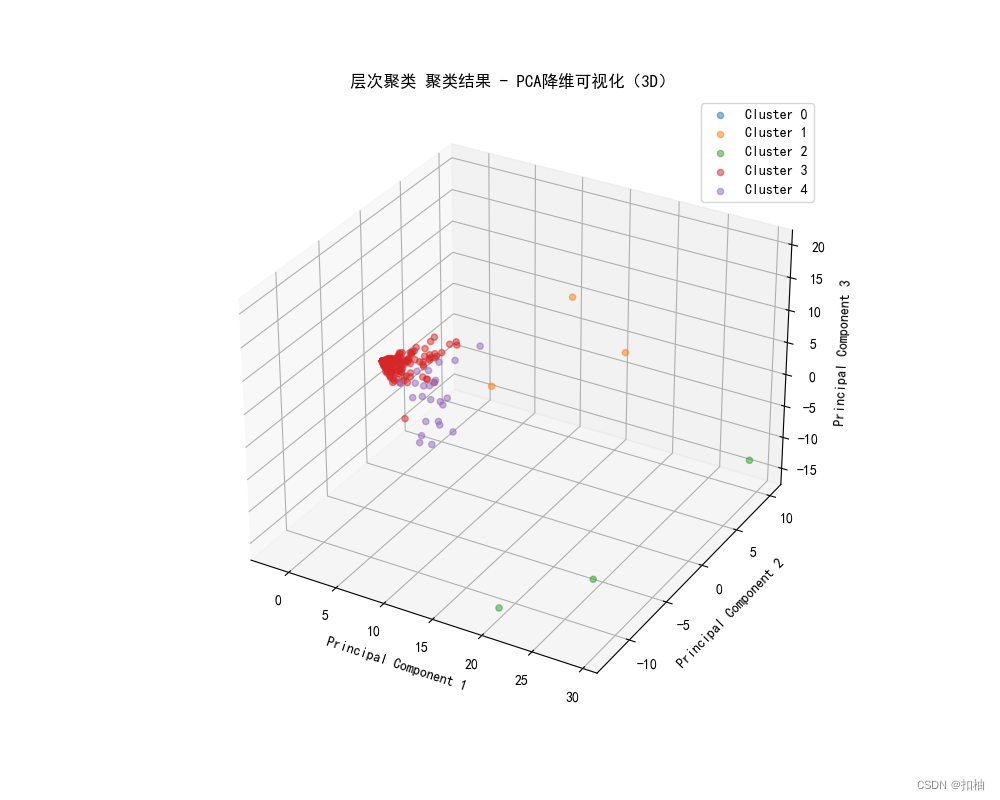
3D可视化

K-Means聚类结果

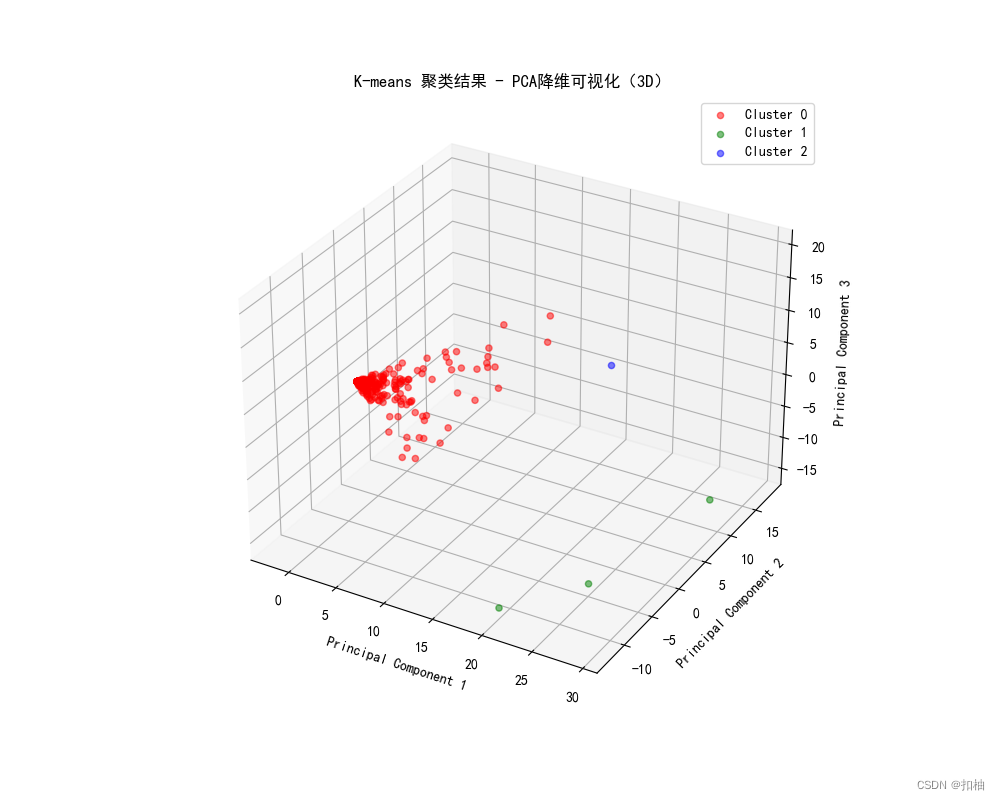
层次聚类结果