机器学习：梯度下降法超详细指南_机器学习 梯度下降

为什么需要梯度下降法

1.梯度下降法是迭代法的一种，可用于求解最小二乘问题。
2.在求解机器学习算法的模型参数，在没有约束条件时，主要有梯度下降法，最小二乘法。
3.在求解损失函数的最小值时，可以通过梯度下降法的迭代求解，求得最小值的损失函数和模型的参数。
4.如果我们需要求解损失函数的最大值，可以通过梯度上升法来迭代，梯度下降法和梯度上升法可以相互转换。
5.在机器学习中，梯度下降法主要有随机梯度下降法和batch梯度下降

为什么梯度方向是下降最快的反方向

一阶导数

在一阶函数中，一阶导数表示函数值与自变量的变化关系，我们把函数从一个点到另一个点变化的函数值与变化的自变量的比值称为函数这两点之间自变量方向的变化率，可以用$\frac{\Delta y}{\Delta x}$表示，当自变量x的变化趋近于0的时候，他们的比值叫做函数的导数，也可以叫做在函数某点沿着自变量变化的斜率。用$tan\Theta$表示。
f ′ ( x ) = lim ⁡ Δ x → 0 f ( x + Δ x ) − f ( x ) Δ χ

$$\begin{aligned}f'\left( x\right) =\lim _{\Delta x\rightarrow 0}\dfrac{f\left( x+\Delta x\right) -f\left( x\right) }{\Delta \chi }\end{aligned}$$ f′(x)=Δx→0lim​Δχf(x+Δx)−f(x)​​

偏导数

接下来，我们把自变量的格局打开（升维），从一元函数上升到多元函数，$z=f(x,y)$,现在我们对一个自变量求导，它反映了多元函数与其中一个自变量的变化关系，也叫做偏导数，他表示函数值在这个点$\Delta x$方向上的变化率。

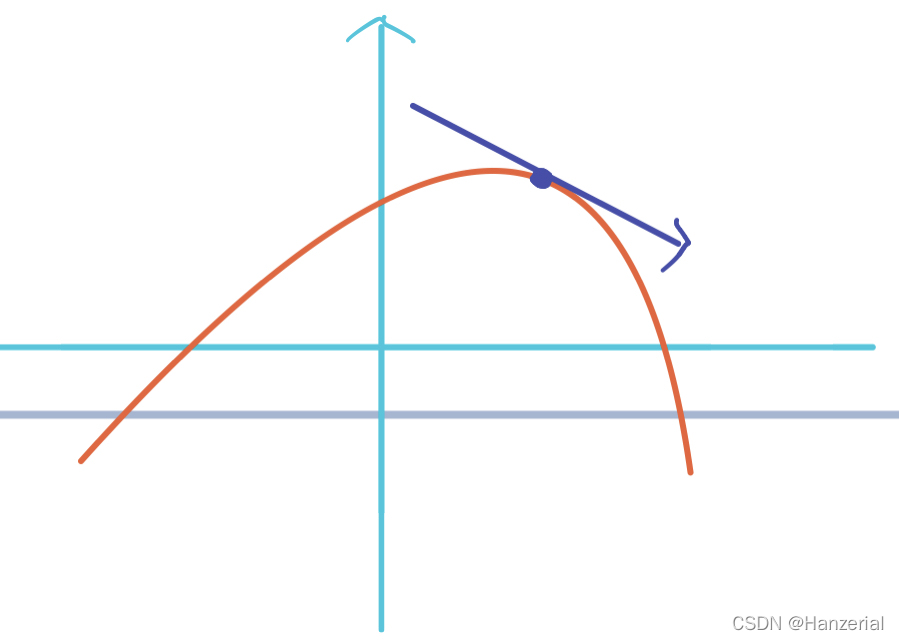
方向导数

看到这里，我们可能会有一个疑问，求导的那个点的方向一定是沿着坐标轴的吗？如图所示，他可以是任意方向。

假设有一个向量l，步长为t，角度为$\Theta$我们要求得函数在l方向上的方向导数，有下图可知，向量l在x轴方向上的改变量为$tsin\Theta$，y轴的改变量为$tcos\Theta$，所以公式可表示为：$$f{\left(x\right)}^{{}^{\prime }}=\underset{t\to 0}{\lim }\frac{f\left(x+t\sin \theta ,y+t\cos \theta \right)-f\left(x,y\right)}{t}$$

梯度

梯度是导数对多远函数的推广，他是对各个自变量偏导数形成的向量，其作用相当于一元函数的导数,之前我们介绍了导数与偏导数，偏导数是一个标量。某个点的梯度代表某个点在多元函数在这点变化方向。
∇ f ( x ) = ( ∂ f ∂ x 1 … ∂ f ∂ x n ) T \nabla f\left( x\right) =

$$\begin{pmatrix} \dfrac{\partial f}{\partial x_{1}} & \ldots & \dfrac{\partial f}{\partial x_{n}} \end{pmatrix}$$ ^{T} ∇f(x)=(∂x1​∂f​​…​∂xn​∂f​​)T

验证

接下来到了最激动人心的时刻，我们来验证为什么函数在这个点的梯度的方向是函数在这个点梯度增加最快的方向。设在某一点在向量l方向的方向导数：
$$f{\left(x\right)}^{{}^{\prime }}=\underset{t\to 0}{\lim }\frac{f\left(x+t\sin \theta ,y+t\cos \theta \right)-f\left(x,y\right)}{t}$$
通过链式法则，化简如下：
= ∂ f ∂ x ⋅ ∂ x ∂ t + ∂ f ∂ y ∂ y ∂ t = sin ⁡ θ ∂ f ∂ x + cos ⁡ θ ∂ f ∂ y

$$\begin{aligned}=\dfrac{\partial f}{\partial x}\cdot \dfrac{\partial x}{\partial t}+\dfrac{\partial f}{\partial y}\dfrac{\partial y}{\partial t}\\ =\sin \theta \dfrac{\partial f }{\partial x}+\cos \theta \dfrac{\partial f}{\partial y}\end{aligned}$$ =∂x∂f​⋅∂t∂x​+∂y∂f​∂t∂y​=sinθ∂x∂f​+cosθ∂y∂f​​
我们要求的变化最快的点，也就是变化率最大，也就是方向导数最大。所以我们就把问题转换成了当上面的化简结果最大时,$\Theta$是多少度，也就知道了在什么方向变化率最大。
我们设向量a=$(sin\theta ,cos\theta )$,向量b=$(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})$
$g(a,b)=ab$
$argma{x}_{\theta }=g(a,b)$
$=|a||b|cos\theta$
$=|b|cos\theta$
因为向量b是不变的，所以当$\theta =0$时，也就是向量a与b（b为梯度）平行时，变化率最大，也就是梯度方向变化最大，从上面结果可知，当$\theta =0$,方向导数一定为正数，所以函数是增函数，所以在这个点的梯度方向，是函数增加最快的方向，相反是最小的方向。

实现过程

梯度下降法也叫做梯度下山法，充分补充了前置知识后，然后在理解梯度下降法，会很简单。梯度是所有偏导数组成的Vector，一个点梯度的方向是函数在这个点增加速度最快的方向（具体证明方法在上面已经展示）。
公式如下：$$F({\theta }_1,{\theta }_2)$$
$${\theta }_{1temp}={\theta }_1-a\frac{\partial f}{\partial {\theta }_1}F({\theta }_1,{\theta }_2)$$
$${\theta }_{2temp}={\theta }_2-a\frac{\partial f}{\partial {\theta }_2}F({\theta }_1,{\theta }_2)$$其中a代表学习率，也就是步长。他代表更新参数时候的步幅迈多大。
重复以上操作，知道${\theta }_1,{\theta }_2$不再变化，这里我们要注意，这两个参数是同时更新，如果先更第一个参数，再用含有第一个更新的参数的函数去更新参数，最后的结果会与梯度下降法有偏差。
我面我们用一个简单地用梯度下降法来优化函数$F({\theta }_1,{\theta }_2)={\theta }_1^2-{\theta }_2^2$在（6，-6）点地参数，来证明梯度下降法。我们可以看出当参数在（0,0）的时候为最小值。
假设a=0.5
$${\theta }_1={\theta }_1-\alpha \frac{\partial f}{\partial {\theta }_1}f\left(x,y\right)=6-0\cdot 1\times 12=4.8$$
$${\theta }_2={\theta }_2-\alpha \frac{\partial f}{\partial {\theta }_1}f\left(x,y\right)=-6-\left(0\cdot 1\times (-12\right))=-4\cdot 8$$
我们发现，经过了一次优化，${\theta }_1,{\theta }_2$原点又接近了一步，这样一直往复下去，参数最终就可以达到原点（假设函数为凸函数）。
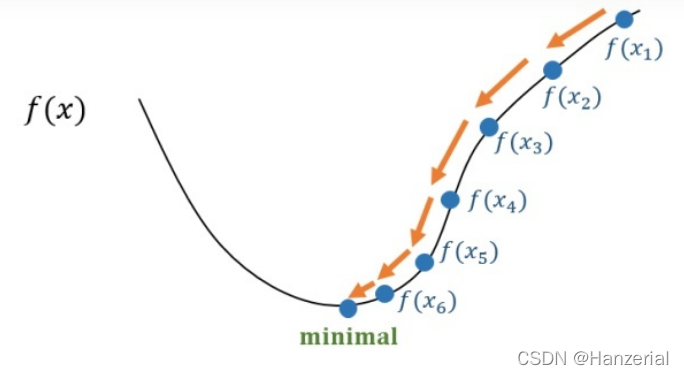
对一个维度的点求偏导数，如果结果为正，则在这点的这一维度为增函数，反之，则相反，我们知道了增减性，我们就知道了，函数往哪个方向走可以让函数的值达到最小。

沿着梯度减小的方向走，梯度会越来越小，我们步长就会越来越小，到达极值点后，梯度达到水平，梯度值接近0，更新的参数也就不再变化。

梯度下降法与最小二乘法的差异

最小二乘法

了解完上面的内容，最后我们要求解W的最优解，需要计算$W=(X^{T}X{)}^{-1}{X}^{T}Y$，重点在于$(X^{T}X{)}^{-1}$，对逆矩阵的求解复杂度是非常高的，加入一个矩阵n*n，如果矩阵为n阶方阵，那么它的时间复杂度为$O(n^3)$，一般$n^3$大于10000就会很慢，我们就会采用梯度下降法求解，如果数据维度太大，计算时间成本也会很大，也会采用梯度下降法。计算时间如果矩阵不可逆，可以采用伪逆的思想求解。如果函数为非凸函数，就会有多个极值点，那么也要采用梯度下降法求解。

梯度下降法

梯度下降法对学习率的选择比较苛刻，不能太大也不能太小，梯度下降法需要进行归一化操作，最小二乘法不需要。如果数据维度小，函数为凸函数，并且矩阵可逆，选用有最小二乘法进行求解。
其次，梯度下降法需要不断的去迭代，来找到一个相对的最优解，速度会慢一些。

局限性

学习率

对学习率的选择比较苛刻，不能太大不能太小，如果太大，更新参数的时候可能会直接跳过极值点，导致变大，越来越大，最后导致梯度爆炸。

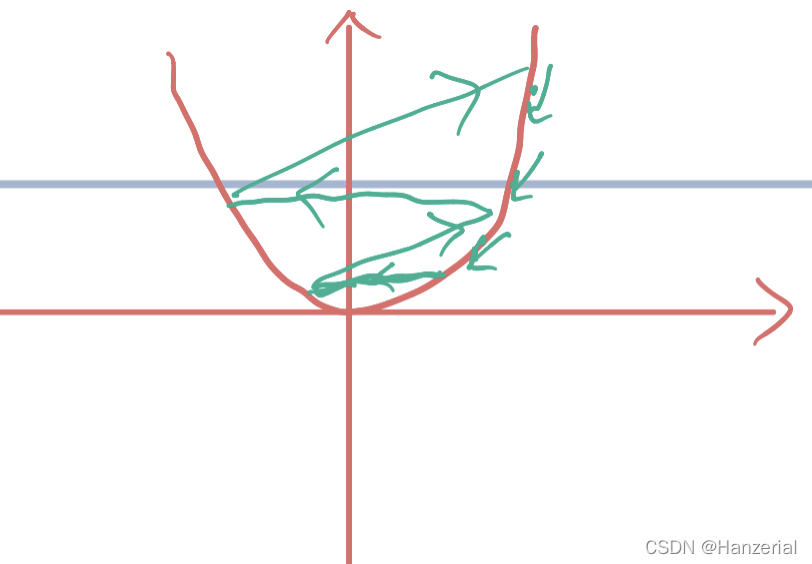
如果学习率太小，会导致学习速度过慢。
在做梯度下降法之前需要对函数进行归一化操作，如果不进行归一化操作，函数找到极值的时间可大大增加。
因为如果观测特征过大，那么我们在反向传播的时候，拿到的梯度就会很大，容易造成局部最优，或者在最优解附近震荡，
如图所示：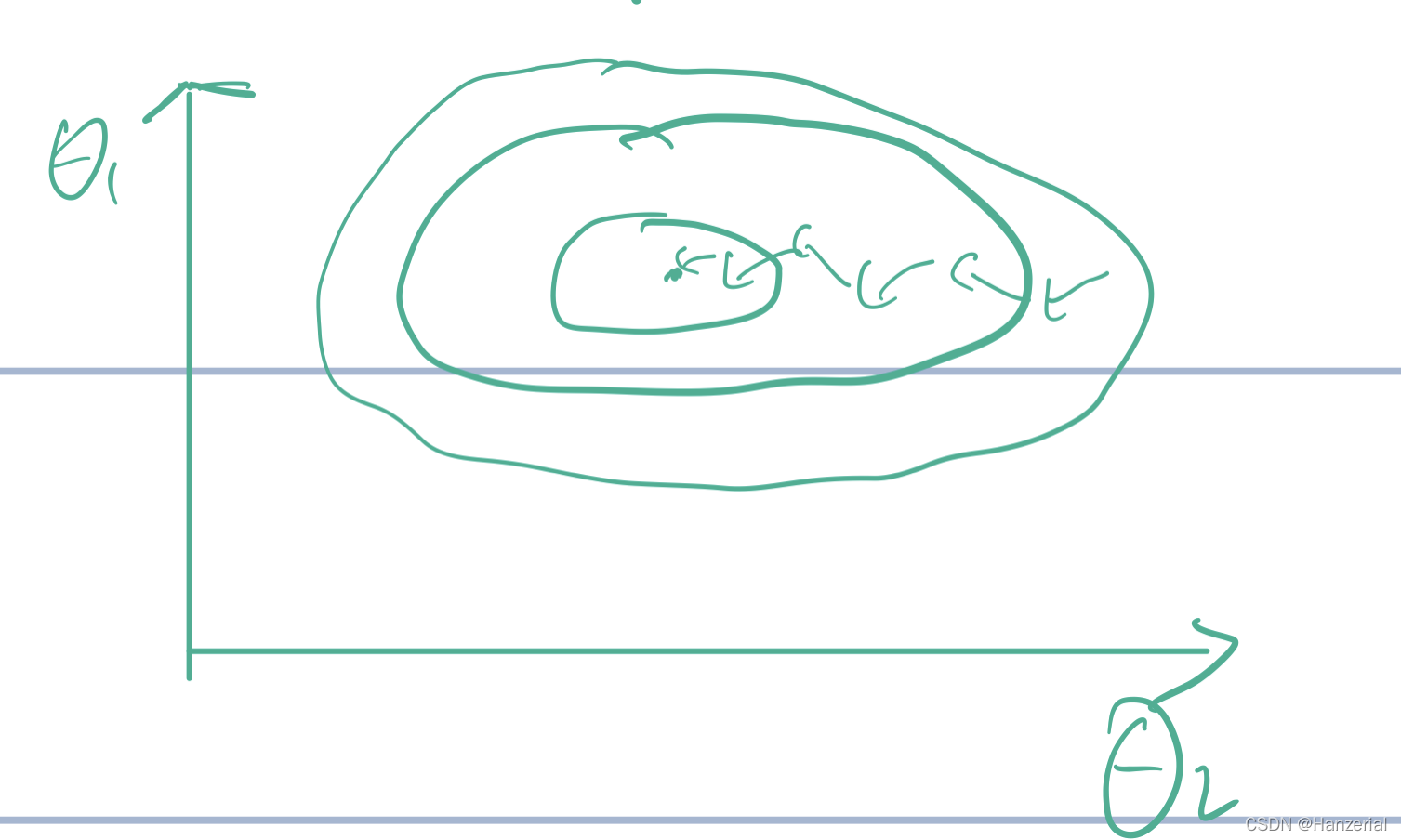
当参数的范围差距不大，等高线图像会更接近于一个圆形，找最优解的需要的时间会大大减少。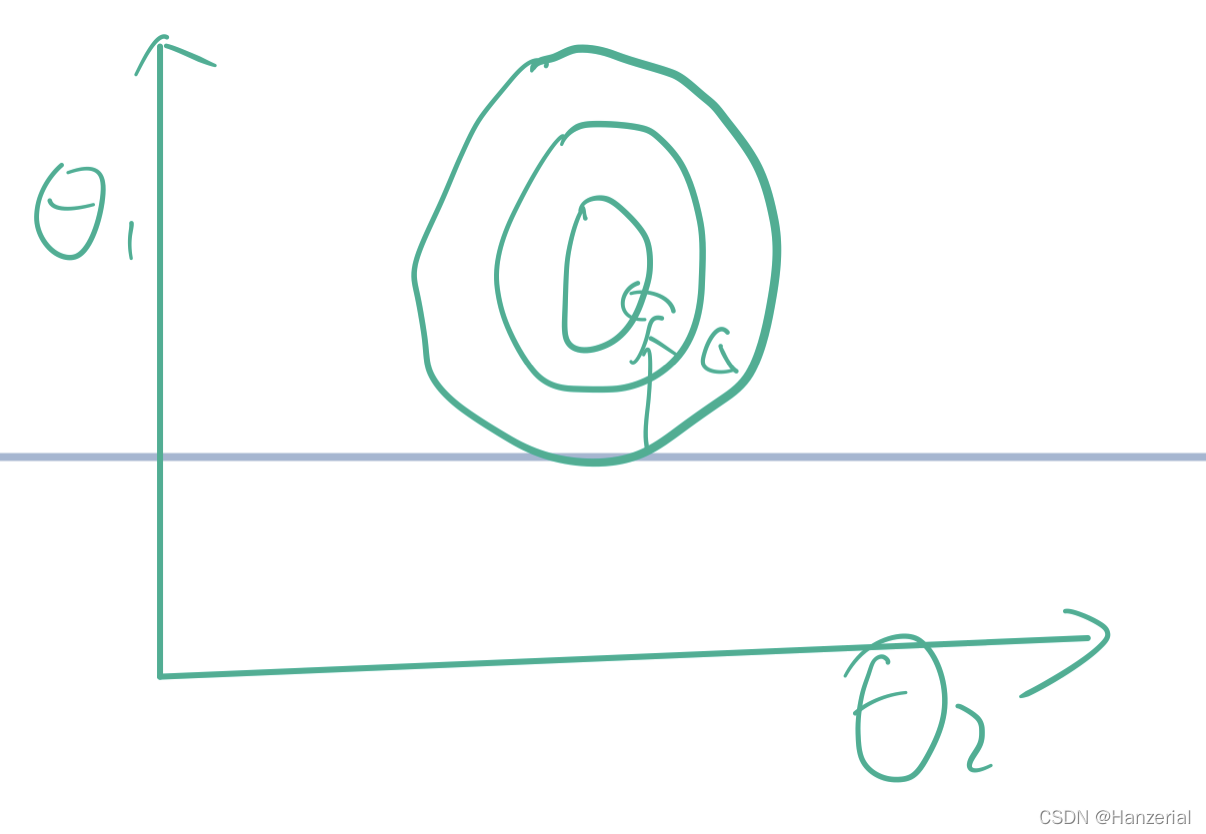

起始点

对起始点值得选择又尤为重要，如果代价函数是一个（非凸函数），那么他的极值点就不唯一，最后的迭代结果可能会是函数得局部最优解。