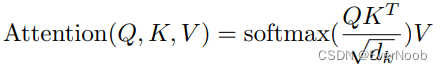1 bit LLM and 1 trit LLM

In light of NV's recent addition of fp4, I'm once again curious about the bottom line for LLM, at least for inference; let's go back to this BitNet paper from Microsoft, featuring 1 bit LLM, with 1-bit weights trained from scatch, and later on another featuring 1.58b or a trit.

Sources

a blog for short summary of 1.58b LLM: https://medium.com/@jelkhoury880/bitnet-1-58b-0c2ad4752e4f

==> a sick comment from which I derived the title

While I am excited by these developments, I really wish they would stop calling it 1-bit. It's not 1 binary bit. It's 1 balanced ternary trit.

==> though do note I think the author's take on its influence on hardware is not quite sound.

One can very well argue that without mmad operations, GPUs or specifically their core SIMT components are once again back in driver seat. It's possible some highly optimized SIMD architecture can utilize the highly structured computation pattern better, but there is no theoretical guarantee for the best case and some misaligned and lopesided shapes will probably favor SIMT instead.

Aiming for better SIMT PPA is challenging NV on its home turf, and it won't be easy to say the least. 

Perhaps more importantly, in the next 3 to 5 years at least, BitNet like structures are more likely to be incorporated into full/half precision networks for partial or inference-only accelerations, than shipped as standalone backbones for main server networks. This reality means a general purpose processor with massive parallelism and a tensor processing unit would still be dominant.

BitNet: Scaling 1-bit Transformers for Large Language Models: https://arxiv.org/pdf/2310.11453.pdf 

The Era of 1-bit LLMs: All Large Language Models are in 1.58 Bits:

https://arxiv.org/pdf/2402.17764.pdf 

1-bit Transformers

Breakdown

Background

The increasing size of large language models has posed challenges for deployment and raised concerns about environmental impact due to high energy consumption.

As the size of these models grows, the memory bandwidth required for accessing and processing the model parameters becomes a major bottleneck, limiting the overall inference performance. Moreover, when deploying these models on distributed systems or multi-device platforms, the inter-device communication overhead can significantly impact the inference latency and energy consumption

Proposal

BitNet, a scalable and stable 1-bit Transformer architecture for LLMs. 

Specifically, BitLinear as a drop-in replacement of the nn.Linear layer in order to train 1-bit weights from scratch.

BitNet employs low-precision binary weights and quantized activations, while maintaining high precision for the optimizer states and gradients during training.

Claim

0. as of 2023.10, "first to investigate quantization-aware training for 1-bit large language models")

1. BitNet achieves competitive performance while substantially reducing memory footprint and energy consumption, compared to state-of-the-art 8-bit quantization methods and FP16 Transformer baselines.

2. BitNet exhibits a scaling law akin to full-precision Transformers. 

3. (minor) better training stability than fp16; can use much larger learning rate for faster convergence

Key statistics

next 4 from figure 1

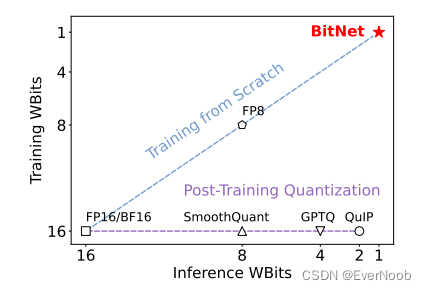
per datum compression; native 1-bit training and inference

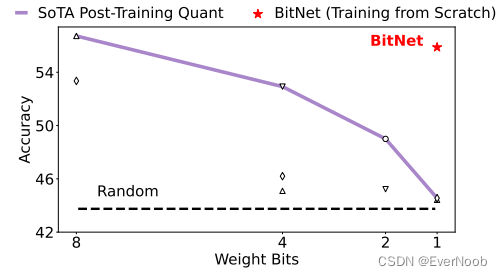
better accuracy than quantization, though not very high in general

Post-Training Quantization vs. Quantization-Aware Training

Most existing quantization approaches for large language models are post-training. They are simple and easy to apply since it does not require any changes to the training pipeline or retraining the model. However, it will result in a more significant loss of accuracy especially when the precision goes lower, because the model is not optimized for the quantized representation during training.

Another strand of quantizing deep neural networks is quantization-aware training. Compared to post-training, it typically results in better accuracy, as the model is trained to account for the reduced precision from the beginning. Moreover, it allows the model to continue-train or do fine-tuning, which is essential for large language models. The challenge of quantization-aware training mainly lies in optimization, i.e., the model becomes more difficult to converge as the precision goes lower. Besides, it is unknown whether quantization-aware training follows the scaling law of neural language models.

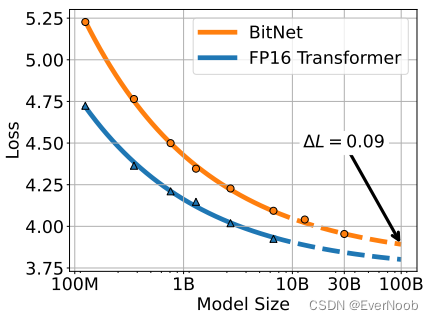
competitive with fp16 model at same size, and showing scaling law, 30B and 100B inferred by fitting power scaling law: 

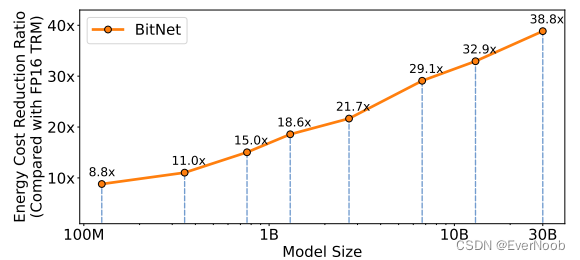
energy efficient, and gain ratio scale with model size (explained later in computation efficiency, there is a catch in that the reduction ratio is a rough power model projection and the BitNet is assumed to only use vectorized processing unit.)

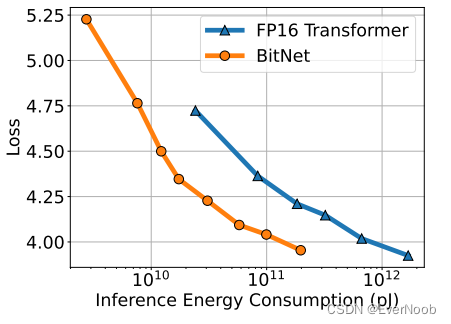
figure3, energy efficient training, used inference energy because "it scales with the usage of the model, while the training cost is only once."

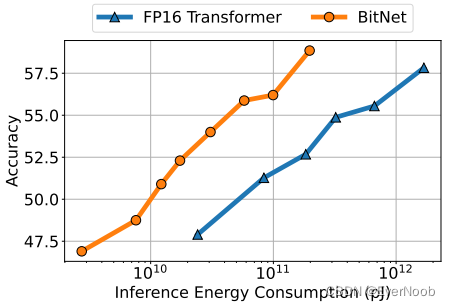
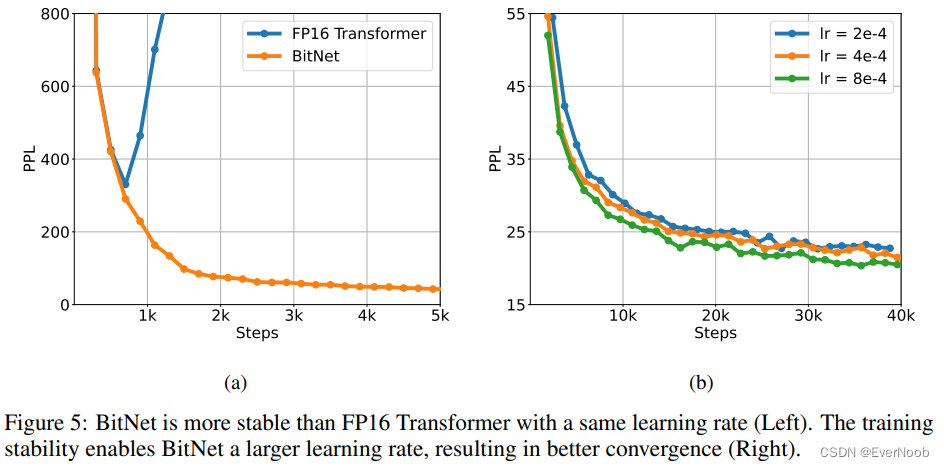
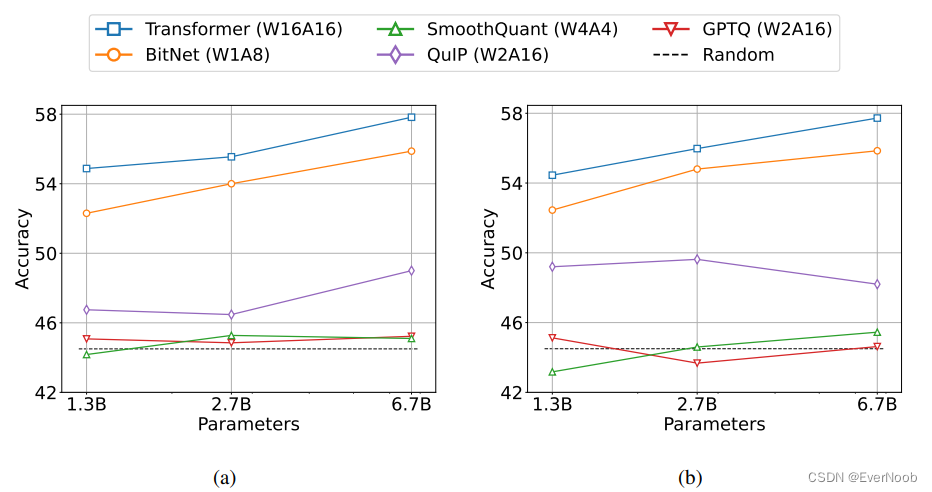
Figure 6: Zero-shot (Left) and few-shot (Right) results for BitNet and the post-training quantization baselines on downstream tasks.

==> FYI, common quantization WxAy or AyWx, x being the bit used for weights and y being bits used for "activation", which simply refers to subsequent computation; in architecture section, by author stated clearly they used 8b for several components, including attention (scaled dot product softmax), and Gelu activation, hence A8W1 for BitNet.

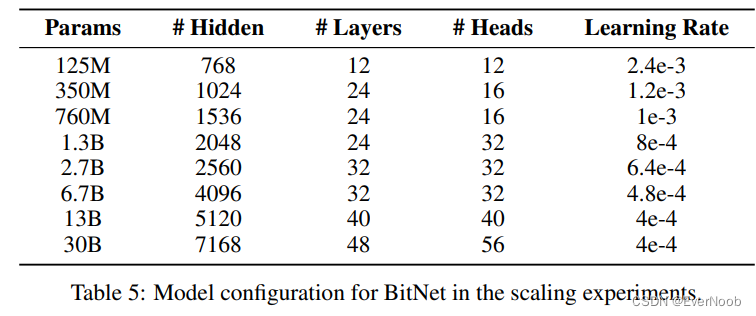
a single head is 64, so more akin to SD than regular LLMs with 128 head size.

Architecture

from figure 2 of the paper

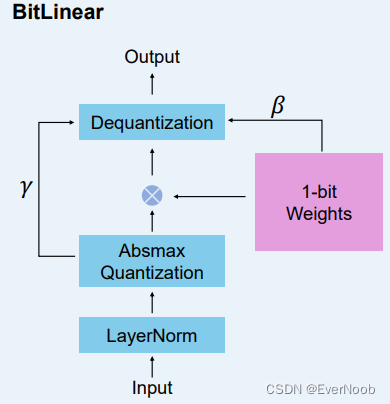
the key component; structurally BitNet features replacement of full/half precision linear layers with binary linear (computation, IO still in higher precision,) layers, as shown below:

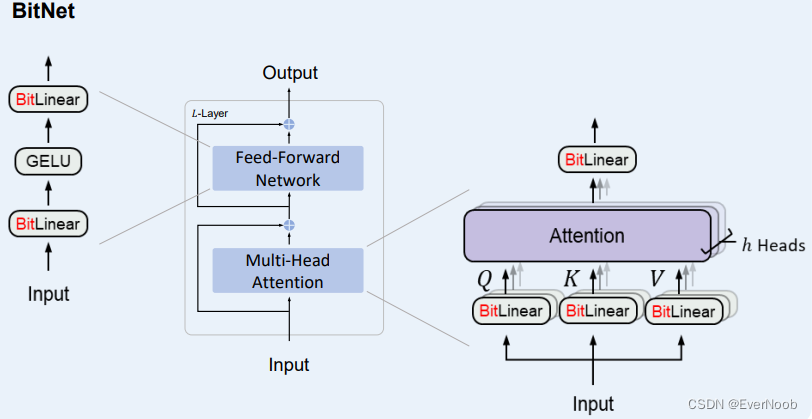
one thing to note here is that Q, K, V mmads (parametric projection) replaced with BitLinear (add)

As shown in Figure 2, BitNet uses the same layout as Transformers, stacking blocks of self-attention and feed-forward networks. Compared with vanilla Transformer, BitNet uses BitLinear (Eq. 11) instead of conventional matrix multiplication, which employs binarized (i.e., 1-bit) model weights.

We leave the other components high-precision, e.g., 8-bit in our experiments. We summarized the reasons as follows. First, the residual connections and the layer normalization contribute negligible computation costs to large language models. Second, the computation cost of QKV transformation (attention) is much smaller than the parametric projection as the model grows larger. Third, we preserve the precision for the input/output embedding because the language models have to use high-precision probabilities to perform sampling.

==> recall from "Attention is All You Need

i.e. parametric projection is determined by model size;

while attention is determined by sequence length (assuming head size is as proposed, always anchored by hidden size)

==> this statement "the computation cost of QKV transformation (attention) is much smaller than the parametric projection as the model grows larger"  is a huge red flag because we do care very much about longer and longer sequence length, as well as model size;

and as a matter of factr, sequence length is grow at a much faster pace than model size.

So the fundamental assumption doesn't really hold, and it shows later all energy efficiency and latency comparison are done with seq_len = 512, therefore rather at odds with current trends.

==> the research still holds decent value in exploring the limit of quantization though,

==> and computation-wise, by reducing memory bound and relocating part of the mmad to pure simd add, even with growing seq_len, we can process the attention part, which is now likely the bound with QKV.

Algorithm: BitLinear

Weight Binarization

binarize the weights to either +1 or −1 with the signum function

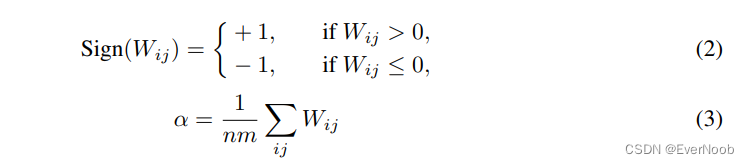
Activation Quantization

the linear matmul is: 

==> we actually shifted mean of w to 0, and only clipped then assumed x has mean 0.

LayerNorm for Training Stability

For the full-precision computation, the variance of the output Var(y) is at the scale of 1 with the standard initialization methods (e.g., Kaiming initialization or Xavier initialization), which has a great benefit to the training stability. To preserve the variance after quantization, we introduce a LayerNorm [BKH16] function before the activation quantization. 

Full Equation 

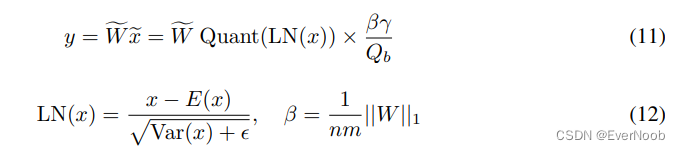
==> do you save pre-binarization weight during training? of cource you must, for sign_num lose you all info. about weight; it's quantization aware training, not quantized training. probably also why they brushed off energy efficiency for training.

Group Quantization and Normalization for Model Parallelism

A prerequisite for the existing model parallelism approaches is that the tensors are independent along the partition dimension. However, all of the parameters α, β, γ, and η are calculated from the whole tensors

One solution is to introduce one all-reduce operation for each parameter. However, even though the communication for each parameter is small, the amount of synchronization is growing as the model becomes deeper, which significantly slows the forward pass.

The problem also exists in SubLN, where the mean and the variance should be estimated across the partition dimension.

We divide the weights and activations into groups and then independently estimate each group’s parameters. 

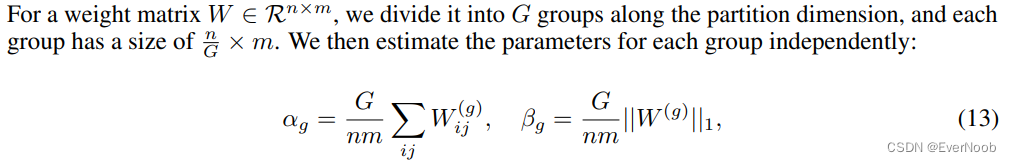
Computation

Parallelism

the actual computation patterns are quite simple, with matmul + SIMD/SIMT parallelism

Efficiency

Arithmetic operations energy. According to the energy model in [Hor14, ZZL22], the energy consumption for different arithmetic operations can be estimated as follows: (table 2)

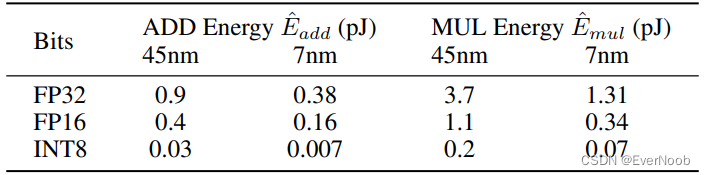
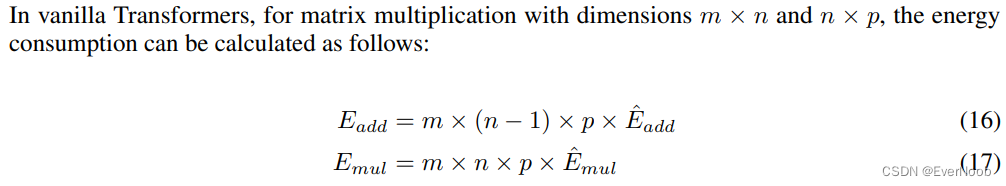
est. energy consumption (seq_len = 512, very small)

Miscellaneous

Training

Straight-through estimator. To train our 1-bit model, we employ the straight-through estimator (STE)[BLC13] to approximate the gradient during backpropagation. This method bypasses the nondifferentiable functions, such as the Sign (Eq. 2) and Clip (Eq. 5) functions, during the backward pass. STE allows gradients to flow through the network without being affected by these non-differentiable functions, making it possible to train our quantized model.

Mixed precision training. While the weights and the activations are quantized to low precision, the gradients and the optimizer states are stored in high precision to ensure training stability and accuracy. Following the previous work [LSL+21], we maintain a latent weight in a high-precision format for the learnable parameters to accumulate the parameter updates. The latent weights are binarized on the fly during the forward pass and never used for the inference process.

1.58b or 1 trit LLM

Breakdown

Proposal

a 1-bit LLM variant, namely BitNet b1.58, in which every single parameter (or weight) of the LLM is ternary {-1, 0, 1}.

Claim

1. matched performance with fp16 (called "full-precision" by the author, let's just say it's baseline precision, since fp32 is normally "full-precision" with fp64 being double-precision, fp16 being half.

matches the full-precision (i.e., FP16 or BF16) Transformer LLM with the same model size and training tokens in terms of both perplexity and end-task performance

2. significantly more cost-effective in terms of latency, memory, throughput,

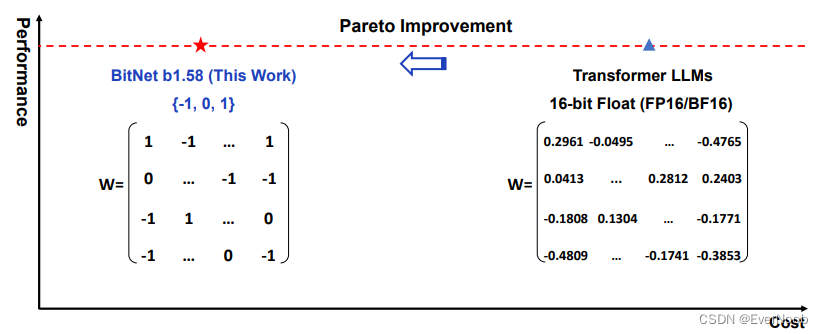
3. and energy consumption

4. defines a new scaling law

5. inspires new hardware design

==> obviously an overly dramatic claim; the most obvious effects for this change is that now we have reduced memory bound and more vector computation to be processed in parallel with tensor computation. This should actually boost performance for long seq_len quite well.

Key Statistics

for hardware performance

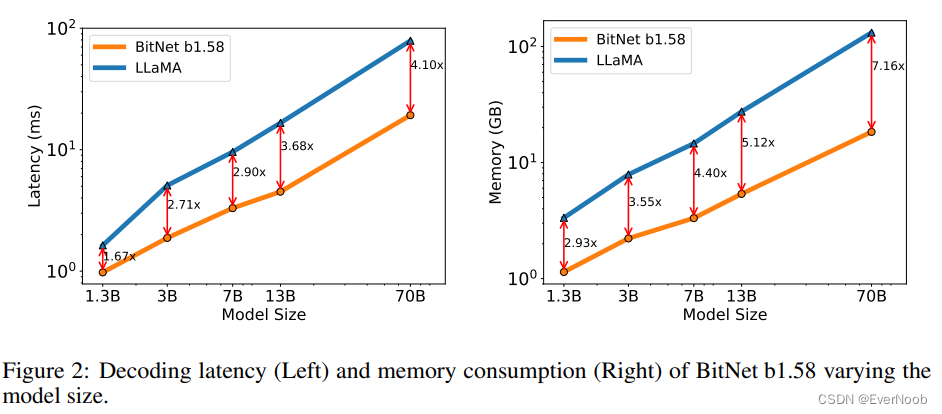
In particular, BitNet b1.58 70B is 4.1 times faster than the LLaMA LLM baseline. This is because the time cost for nn.Linear grows with the model size.

==> "while the percentage of nn.Linear grows with the model size, while the cost from other components is smaller for larger models." ==> suggesting again, using small seq_len for test points

The memory consumption follows a similar trend, as the embedding remains full precision and its memory proportion is smaller for larger models. Both latency and memory were measured with a 2-bit kernel, so there is still room for optimization to further reduce the cost.

We compare the throughput of BitNet b1.58 and LLaMA LLM with 70B parameters on two 80GB A100 cards, using pipeline parallelism [HCB+19] so that LLaMA LLM 70B could be run on the devices. We increased the batch size until the GPU memory limit was reached, with a sequence length of 512. Table 3 shows that BitNet b1.58 70B can support up to 11 times the batch size of LLaMA LLM, resulting an 8.9 times higher throughput

==> this shows very likely all benchmarks are taken with seq_len = 512

for matching precision at 3B

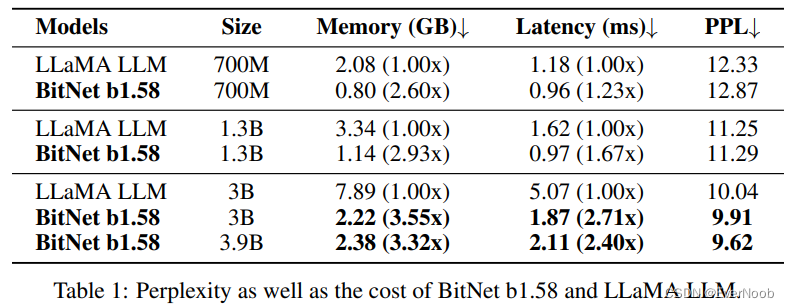
for energy efficiency

Figure 3: Energy consumption of BitNet b1.58 compared to LLaMA LLM at 7nm process nodes. On the left is the components of arithmetic operations energy. On the right is the end-to-end energy cost across different model sizes.

==> pls note the left graph is simply a per instruction cost compare, not a stat-total compare; the presentation and phrasing is misleading. 

Architecture

same as 1b BitNet, but

1. replace sign_num with absmean

2.  do not scale the activations before the non-linear functions to the range [0, Qb]. Instead, the activations are all scaled to [−Qb, Qb] per token to get rid of the zero-point quantization. This is more convenient and simple for both implementation and system-level optimization, while introduces negligible effects to the performance in our experiments.

3. now with LLaMA components:

BitNet b1.58 adopts the LLaMA-alike components. Specifically, it uses RMSNorm [ZS19], SwiGLU [Sha20], rotary embedding [SAL+24], and removes all biases. 

Algorithm: absmean quantization

first scales the weight matrix by its average absolute value, and then round each value to the nearest integer among {-1, 0, +1}: