数字IC经典电路（4）——经典滤波器的实现（滤波器简介及Verilog实现）_数字滤波如何实现

写在前面的话

数字滤波器一般可以分为两类：有限冲激响应（FIR）滤波器和无限冲激响应（IIR）滤波器。

在Verilog综合方面，通常可以实现四种数字滤波器：

1. 基于时域采样的FIR滤波器（Time Domain Sampling FIR Filter）
2. 快速傅里叶变换（FFT）算法实现的FIR滤波器（FFT-based FIR Filter）
3. 直接IIR滤波器（Direct Form IIR Filter）
4. 级联IIR滤波器（Cascade IIR Filter）

其中，基于时域采样的FIR滤波器适用于低通、高通、带通、带阻等常见滤波器类型，但其抗混叠能力较差；FFT-based FIR滤波器适用于平滑频率特性要求高的滤波器，但需要额外硬件支持FFT运算；直接IIR滤波器和级联IIR滤波器适用于需要更少延迟和低硬件成本的滤波器设计，但容易出现稳定性问题。

数字滤波器分类

数字滤波器是一种数字信号处理技术，用于对数字信号进行去噪、滤波和频谱分析等处理。根据其响应特性和算法实现方式，数字滤波器可以分为多种类型。

1. FIR滤波器

FIR滤波器是一种有限冲激响应（Finite Impulse Response）滤波器，具有线性相位、无回声等特点，常用于需要精确控制滤波器通带和阻带幅度响应的应用中，如语音和音频处理、图像处理和通信系统中的调制解调等。

2. IIR滤波器

IIR滤波器是一种无限冲激响应（Infinite Impulse Response）滤波器，可以通过递归方式获得稳定性，具有较低的阶数和更好的全通性能，适用于带限信号处理和模拟滤波器的数字实现。

3. 频域滤波器

频域滤波器是基于傅里叶变换等频域分析技术设计的滤波器，包括低通、高通、带通和带阻四种类型，可用于滤波器设计、频域分析和信号还原等方面。

4. 自适应滤波器

自适应滤波器是一种能够根据输入信号和环境的变化自行调整滤波系数的滤波器，主要用于去除噪声和复杂的干扰。

5. 数字时域处理滤波器

数字时域处理滤波器是利用离散时间信号的离散微分、差分或积分等进行信号滤波的滤波器，常见的有均值滤波器、中值滤波器和高斯滤波器等。

以上各种数字滤波器的选择取决于应用场景和设计要求，需要综合考虑其性能、稳定性、响应速度和资源消耗等因素。

经典数字滤波器

FIR滤波器

普通FIR滤波器实现方案

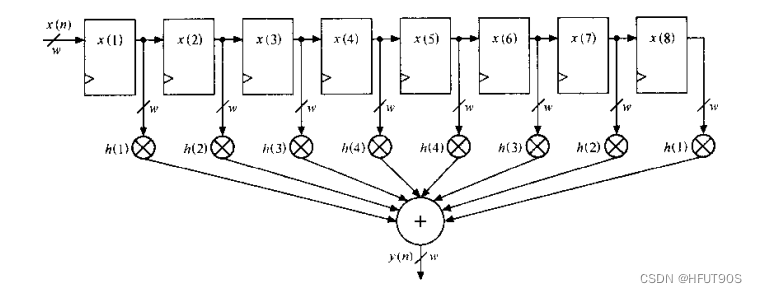
线性相位的FIR滤波器结构图

FIR特点及注意点
FIR滤波器（Finite Impulse Response Filter，有限脉冲响应滤波器）的特点：

1. FIR滤波器具有稳定、线性和时不变的特性，能够精确控制频率响应。

2. FIR滤波器计算简单，容易实现。

3. 理论上，FIR滤波器能够完全去除滤波器输入信号中的周期性干扰。

4. FIR滤波器具有简单的调整滤波器特性的方式，只需要简单地添加或减少滤波器的系数并重新编程即可。

在Verilog设计FIR滤波器时需要注意以下几点：

1. 定义好滤波器的系数，FIR滤波器的效果和性能主要取决于这些系数。在计算系数时，请使用MATLAB或其他专业工具来保持准确性。

2. 确定输入/输出数据的宽度，这通常需要根据具体应用来确定。您需要考虑您的信号源的噪声和分辨率，并设置数据宽度以确保不会有过多的噪声或失真。

3. 确定时钟频率，这也需要根据该设计中的最大数据速率来确定。如果时钟周期不足以处理所有输入数据，则需要增加时钟频率或引入流水线来处理。

4. 注意FIR滤波器延迟的问题。由于FIR滤波器中的系数乘法运算是串行的，会导致输出数据的延迟。您需要在设计中考虑这个因素，并相应地调整时序。

5. 经过设计和仿真后，需要进行一些性能测试来确保您的FIR滤波器在实际使用中能够按预期工作。请特别注意过高的噪声和失真，这些问题通常可以通过调整系数、增加时钟频率等方式来解决。
   Verilog代码 example1

module fir_filter 
#(
  parameter WIDTH = 16, // 数据位宽
            COEFF_SIZE = 5, // 系数位宽
            TAP_NUM = 10 // 块大小或阶数
)
(
  input clk,
  input rst,
  input signed [WIDTH-1:0] din,
  output reg signed [WIDTH-1:0] dout
);

reg signed [WIDTH-1:0] shift_reg [0:TAP_NUM-1];
reg signed [COEFF_SIZE-1:0] coeff [0:TAP_NUM-1];

integer i;
integer j;
reg signed [WIDTH+COEFF_SIZE-2:0] sum;

initial begin
  for (i=0; i < TAP_NUM; i=i+1) begin
    shift_reg[i] <= 0;
    coeff[i] <= 'd1 ;
  end
  dout <= 0;
end

always @(posedge clk or posedge rst) begin
  if (rst) begin
    dout <= 0;
    sum <= 0;
    for (i=0; i<TAP_NUM; i=i+1) begin
      shift_reg[i] <= 0;
    end
  end else begin
    //移位寄存器,最新元素放在第一位
    for (i=TAP_NUM-1; i>0; i=i-1) begin
      shift_reg[i] <= shift_reg[i-1];
    end
    shift_reg[0] <= din;

    //计算权值和
    
    for (j=0; j<TAP_NUM; j=j+1) begin
      sum <= sum + (shift_reg[i] * coeff[i]);
    end

    dout <= sum[WIDTH-1:0];
  end
end

endmodule
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

example1仿真波形

Verilog代码 example2

module FIR_Filter(clk, reset, data_in, data_out);

parameter N = 16;

input clk, reset;
input [N-1:0] data_in;
output reg [N-1:0] data_out; 

// coe defination
wire [5:0] b0 =  6'b100000; 
wire [5:0] b1 =  6'b100000; 
wire [5:0] b2 =  6'b100000; 
wire [5:0] b3 =  6'b100000;
wire [N-1:0] x1, x2, x3; 

//  D Flip Flops
DFF DFF0(clk, 0, data_in, x1); // 
DFF DFF1(clk, 0, x1, x2);      //
DFF DFF2(clk, 0, x2, x3);      // 

//  Multiplication
wire [N-1:0] Mul0, Mul1, Mul2, Mul3;  
assign Mul0 = data_in * b0; 
assign Mul1 = x1 * b1;  
assign Mul2 = x2 * b2;  
assign Mul3 = x3 * b3;  
 
// Addition operation
wire [N-1:0] Add_final; 
assign Add_final = Mul0 + Mul1 + Mul2 + Mul3; 

// Final calculation to output 
always@(posedge clk)
data_out <= Add_final; 

endmodule

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

example2仿真波形（正弦滤波）

FFT—FIR滤波器

基于FFT的FIR数字滤波器是一种广泛使用的数字滤波方法，它使用FFT算法对FIR滤波器的频率响应进行计算，以实现滤波器功能。FIR数字滤波器具有以下优缺点：

优点：

1. 它具有很高的精度和稳定性。FFT算法可以实现非常高的精度和灵敏度，并且在信号噪声较高时也非常稳定。

2. FFT算法的计算速度很快，而且还可以使用硬件加速器来进一步提高计算性能。

3. 这种滤波器可以实现非常窄的带通和带阻滤波器，以达到更精确的控制和调整滤波器特性。

4. FIR滤波器的系数是固定的，所以在进行信号处理时可以更容易地调整数据存储器。

缺点：

1. FFT算法需要一个大量的存储器来存储信号输入和输出数据，这通常会对系统的处理速度产生很大影响。

2. 由于FFT算法需要将所有输入数据一次性处理完毕，因此在信号输入速度超过系统处理能力时，系统将无法按照预期输出。

3. 与其他数字滤波器相比，基于FFT的FIR数字滤波器需要对输入信号采样进行大量的信号预处理，所以它对输入信号采样的要求较高。

基于FFT的FIR数字滤波器具有高精度、高稳定性和滤波调整灵活等多个优点，但也存在一些缺陷，如需要大量的存储器以及对输入信号采样的要求较高。

顺序结构FFT

顺序结构是根据 FFT 中每个蝶形运算单元计算的先后顺序。其典型结构如图 所示，顺序结构中仅包含一个蝶形运算单元和一个存储单元，每级运算单元使用同一个蝶形运算单元，且所有输入数据、每级运算结果及输出结果均使用同一个存储单元。

流水线结构FFT

流水结构的 FFT 将 FFT 计算分解为 M 个子过程，M 即为 FFT 计算的级数。每级采用独立的蝶形运算单元，各级蝶形运算单元先将计算结果传输至下一级，然后再接收上一级的数据进行计算，使 FFT 计算过程以流水的方式进行，增加 了FFT 的计算速度。

并行结构FFT

在 FFT 每级中采用 M 个蝶形运算单元同时计算，提升了 FFT 计算速度。FFT并行结构计算速度快，具有高吞吐量，采用多个蝶形运算单元同时计算，相比于只采用一个蝶形运算单元计算，速度是成倍增加的；速度增加，导致了并行计算的 FFT 需要消耗更多的计算资源和存储资源。

阵列结构FFT
阵列结构全并行的计算特点决定了其计算速度比并行结构和流水结构要快，同时也意味着其具有远超于并行结构和流水结构的资源消耗。

FFT-based FIR Filter example1

module fft_filter(
    input [7:0] in_data,
    output reg [7:0] out_data
);

parameter signed [3:0] tw_re = 8'h0F; // 1/sqrt(2)
parameter signed [3:0] tw_im = -8'h0F; // -1/sqrt(2)

reg signed [3:0] x_real, x_imag;
reg signed [3:0] y_real, y_imag;

always @* begin
    // Calculate first stage of FFT
    x_real = in_data[3:0];
    x_imag = 4'h0; // zero-padding imaginary part
    y_real = x_real + (tw_re * in_data[7:4]) - (tw_im * 4'h0);
    y_imag = (tw_re * 4'h0) + (tw_im * in_data[7:4]) + 4'h0;

    // Calculate second stage of FFT
    x_real = y_real;
    x_imag = y_imag;
    y_real = x_real + (tw_re * 4'h0) - (tw_im * y_imag);
    y_imag = (tw_re * y_imag) + (tw_im * 4'h0) + 4'h0;

    // Output magnitude of second stage
    out_data = {y_real[3:0], y_imag[3:0]} ^ 8'hFF; // invert MSB for magnitude display
end

endmodule

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

example仿真波形

并行FIR滤波器

并行FIR数字滤波器是一种数字信号处理器件，它能够高效地进行数字信号滤波操作。与串行FIR数字滤波器不同，它可以同时处理多个输入样本，从而实现更快的运算速度和更高的吞吐量。

并行FIR数字滤波器通常采用多个滤波器核心并行工作，每个核心负责处理一个输入样本，并将处理结果汇总以生成输出数据。这种并行处理方式可以利用现代并行计算架构的优势，例如GPU或FPGA等，从而显著提高数字滤波的处理速度和效率。

并行FIR数字滤波器的主要优点包括：

1. 高效的运算速度：采用并行计算方式，使得多个输入样本可以同时被处理，大幅提高了数字滤波的运算速度。
2. 高性能的吞吐量：并行FIR数字滤波器可以在相同的时间内处理更多的输入样本，从而提高了数字滤波的吞吐量。
3. 可扩展性强：由于并行FIR数字滤波器采用多个滤波器核心并行计算，因此具有很好的可扩展性，可以根据需要增加处理核心来提高滤波器的处理能力。

但并行FIR数字滤波器也存在一些缺点：

1. 设计难度较大：由于并行FIR数字滤波器需要多个滤波器核心协同工作，因此需要较高的硬件设计及算法优化技术。这对于初学者来说可能比较困难。
2. 硬件成本相对较高：并行FIR数字滤波器通常需要更多的硬件资源来实现，并且需要更复杂的控制逻辑，因此在实际应用中可能需要更高的成本支出。
   下图为并行结构的FIR滤波器：
   
   Verilog代码 example

查看菜鸟教程中并行FIR滤波器的代码：

modelsim仿真波形，高频滤波：

串行FIR滤波器

串行FIR数字滤波器是由一系列单级FIR数字滤波器级联构成。它的输入信号经过第一个FIR滤波器后，输出作为下一个FIR滤波器的输入，以此类推直到输出最终结果。串行FIR数字滤波器被广泛应用于音频处理、图像处理和通信系统中。

优点：

1. 串行FIR数字滤波器结构简单，易于实现，并且具有稳定性和可靠性。
2. 串行FIR数字滤波器具有高阶滤波器特性，可以实现更高的滤波器阶数。
3. 串行FIR数字滤波器可以实现多通道滤波器，适用于多通道信号处理。

缺点：

1. 串行FIR数字滤波器的延迟相对较高，可能会导致对实时性要求较高的应用存在问题。
2. 串行FIR数字滤波器需要更多的计算资源来实现高阶滤波器。
   串行FIR滤波器结构：

Verilog代码 example

菜鸟教程，串行FIR滤波器；

CSDN，jk_101博客

CIC滤波器

CIC数字滤波器是一种高效的数字滤波器，用于降低采样率。它通过组合积分器和累加器来实现，可实现非常高的抽取因子，并且不需要在滤波器中使用乘法器或除法器。

CIC数字滤波器的优点包括：

1. 高效性：由于CIC滤波器只使用加法器和移位器，因此它们可以在硬件中容易地实现，而无需使用乘法器或除法器。
2. 抗混叠能力强：CIC滤波器对输入信号的高频成分具有很好的抑制效果，这使得它们非常适合用于抽取信号中高频噪声的应用。
3. 占用资源少：由于CIC滤波器的简单结构，它们需要的资源相对较少，因此可以在小型FPGA或ASIC中实现。

CIC数字滤波器的缺点包括：

1. 滞后：由于CIC滤波器的设计原理，它们会引入一定的滞后，这可能会对某些应用程序产生影响。
2. 灵敏度：当输入信号变化较小时，CIC滤波器可能会出现较大的输出变化，这可能会导致一些应用程序的精度下降。

在使用verilog设计CIC数字滤波器时，需要注意以下几点：

1. 输入信号的位宽应与滤波器的位宽匹配。
2. CIC滤波器中的加法器和移位器可以通过verilog语言中的"+=“和”>>"运算符轻松实现。
3. 在verilog代码中，需要注意最后一级积分器输出的值可能会超过位宽范围，因此需要进行截断或饱和处理。
4. 由于CIC滤波器的结构比较特殊，因此在verilog中实现时需要仔细考虑其各个部分之间的关系。

五级CIC滤波器：

Verilog代码 example

菜鸟教程，CIC滤波器

卡尔曼滤波器

数字卡尔曼滤波器是一种基于贝叶斯滤波理论的递归算法。它的核心思想是将系统状态和观测数据视为随机变量，利用已知的系统模型和测量模型，通过考虑先验信息和实际测量值来更新状态估计值，从而使得最终的估计值具有更高的准确性。

卡尔曼滤波器中包含两个重要的方程：状态预测方程和状态更新方程。状态预测方程描述了系统状态如何根据前一个时刻的状态和外部控制输入进行预测，并估计预测误差的协方差；状态更新方程描述了如何根据当前时刻的测量值和预测值来更新估计值，并估计更新后的状态误差的协方差。

数字卡尔曼滤波器的优点主要包括以下几个方面：

1. 核心算法简单易懂：卡尔曼滤波器的核心思想非常简单，容易掌握和实现。
2. 适应各种噪声条件：卡尔曼滤波器可以有效地处理多种噪声类型，包括高斯白噪声、偏差噪声等。
3. 高效性：卡尔曼滤波器仅需要存储和更新当前状态的估计值和协方差矩阵，而不需要维护完整的历史数据，因此具有较高的计算效率。

数字卡尔曼滤波器也存在一些缺点：

1. 对系统模型和测量模型要求高：卡尔曼滤波器需要准确的系统信息和观测数据，如果这些信息存在误差或不确定性，将影响卡尔曼滤波器的估计效果。
2. 不适用于非线性系统：卡尔曼滤波器是一种线性滤波器，在处理非线性系统时可能无法达到很好的效果。
3. 过去信息权重过大：由于卡尔曼滤波器的递推方式，每一次状态更新都充分考虑了过去的所有信息，因此过去信息对估计结果的影响比较大，导致滤波器反应比较慢。

Verilog代码：

//只是一个简单的卡尔曼滤波器
module kalman_filter(
    input clk,
    input resetn,
    input [3:0] measurement,
    output reg [3:0] kf_output
);

parameter R = 2; // 测量噪声方差
parameter Q = 1; // 状态噪声方差

reg signed [3:0] x_hat_prev; // 上一时刻状态估计值
reg signed [3:3] P_prev; // 上一时刻状态协方差矩阵
reg signed [3:0] K; // 卡尔曼增益
reg signed [3:0] x_predict;
reg signed [3:3] P_predict;
reg signed [3:0] innovation;
always @(posedge clk or negedge resetn) begin
    if (resetn == 1'b0) begin
        x_hat_prev <= 4'sd0;
        P_prev <= {4{4'sd1}};
        K <= 4'sd0;
        kf_output <= 4'sd0;
    end else begin
        // 状态预测
         x_predict = x_hat_prev;
         P_predict = P_prev + Q;

        // 更新卡尔曼增益
        K = P_predict / (P_predict + R);

        // 更新状态估计和协方差矩阵
        innovation = measurement - x_predict;
        x_hat_prev = x_predict + K * innovation;
        P_prev = (1 - K) * P_predict;

        // 输出状态估计值
        kf_output <= x_hat_prev;
    end
end

endmodule
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

modelsim仿真波形

总结

滤波器是一种用于信号处理的重要工具，常用于滤除噪声、去除干扰和改善信号质量。以下是关于FIR滤波器、基于FFT的FIR滤波器、并行FIR滤波器、串行FIR滤波器、CIC滤波器以及卡尔曼滤波器的总结：

1. FIR滤波器是一种非递归滤波器，可以对信号进行线性相应。适用于需要较长冲激响应的数字滤波器。
2. 基于FFT的FIR滤波器是一种通过快速傅里叶变换（FFT）实现的FIR滤波器，适用于需要实时滤波且具有高计算效率的场合。
3. 并行FIR滤波器是一种将输入数据分成多路并在每一路上并行处理以提高计算效率的滤波器。适用于需要高速、高性能、多通道处理的系统。
4. 串行FIR滤波器是一种将输入数据串联到每个阶段的简单滤波器中进行连续处理的滤波器。适用于低速且资源有限的系统。
5. CIC滤波器是一种特殊的IIR滤波器，适用于对高速采样率信号进行降采样处理。CIC滤波器具有低延迟和低计算复杂度的优点，但是在频率选择性方面可能不如FIR滤波器。
6. 卡尔曼滤波器是一种运用贝叶斯概率理论进行状态估计和数据处理的滤波器，适用于需要将多个测量值组合在一起获得更准确的状态信息的系统，例如惯性导航和目标跟踪。

各种滤波器的适用范围相对较宽，最终的应用还需根据具体情况进行选择。滤波器的设计更偏向于算法和信号处理，本人涉及的相关知识点较少，感兴趣的同学可以参考杜勇老师编著的《数字滤波器的Matlab于FPGA实现》。也欢迎广大通信相关的同僚批评指正以及分享资料，感谢！

参考资料

[1]王海淼. 基于FPGA的实时FFT分析方法研究[D].哈尔滨工业大学,2021.DOI:10.27061/d.cnki.ghgdu.2021.002691.
[2]杜勇. 数字滤波器的MATLAB与FPGA实现.第2版[M]. 电子工业出版社, 2014.
[3]https://www.runoob.com/w3cnote/verilog-serial-fir.html
[4]https://blog.csdn.net/jk_101/article/details/129148406