【二叉树】遍历与创建 前序中序后续 递归实现_后续递归建立二叉树

树基本概念

         二叉树：每个结点最多只能有2个子树，如下图所示：

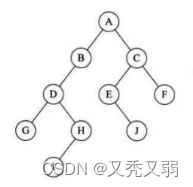
遍历二叉树：

• 分类

        （1）先序遍历：根 ->左 ->右 的顺序 先遍历根节点，再遍历左子树，最后遍历右子树，如下图所示。

       

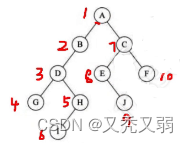
 图示为举例进行先序遍历顺序

        （2）中序遍历：左 -> 根 ->右的顺序。

        （3）后序遍历：左 -> 右-> 根的顺序

        （4）层次遍历：从上到下、从左到右的顺序，如图所示：

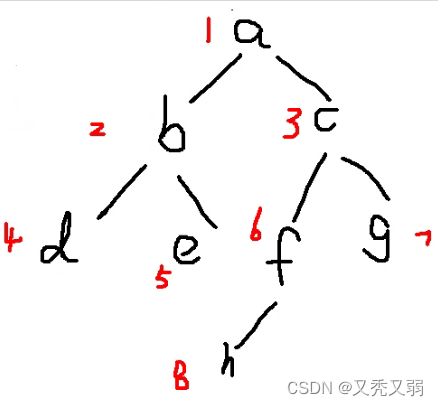
 图示为举例进行层遍历顺序

• 先序、中序、后序递归遍历代码（文章最底部有完整代码）

递归实现

//先序遍历输出二叉树
//先、中、后都是针对于根而言所起的名字
void PreOrder(node* root)
{
    if (root != NULL)
    {
        printf("%c", root->value);
        PreOrder(root->left);
        PreOrder(root->right);
    }
}
 
//后序
void PostOrder(node* root)
{
    if (root != NULL)
    {
        PostOrder(root->left);
        PostOrder(root->right);
        printf("%c", root->value);
    }
}
//中序
void InOrder(node* root)
{
    if (root != NULL)
    {
        InOrder(root->left);
        printf("%c", root->value);
        InOrder(root->right);
    }
}

• 层次遍历

• 先序、中序、后序非递归遍历

        

创建二叉树：

• 方式

•         先序遍历创建：根 ->左 ->右 的顺序

          中序遍历创建：左 -> 根 ->右的顺序

          后序遍历创建：左 -> 右-> 根的顺序

• 首先对原始二叉树用 * 补为完全二叉树（包括叶子节点也要补上左右子树），如下右图所示：

 

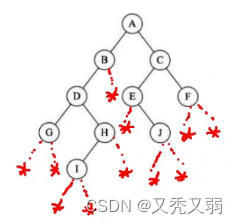
• 然后根、左、右（该处举例先序遍历方式创建）的顺序进行提取数据：A B D G * * H I * * * * C E * J * * F * *
• 递归思想创建的思路演绎：
•   步骤： 从跟开始赋值，然后依次是左孩子、右孩子的顺序。遇到 * 时，赋值为NULL，然后往上走。具体操作如下所示：

        原始数据：A B D G * * H I * * * * C E * J * * F * *

        第一次遇到 * ：* * H I * * * * C E * J * * F * *，形成如下图所示的二叉树，将G的左右孩子赋值为NULL后，向上走，顺次该对D的右孩子赋值...

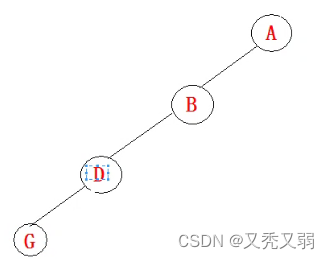
        第二次遇到*： * * * * C E * J * * F * *，形成如下图所示的二叉树，将I的左右孩子赋值为NULL后，向上走，顺次该对H的右孩子赋值为NULL，然后对B的右孩子赋值为NULL，紧接着将C赋值到A的右孩子位置...

        第三次遇到*： * J * * F * *，形成如下图所示的二叉树，将E的左孩子赋值为NULL后，将J赋值给右孩子位置...

        第四次遇到*： * * F * *，形成如下图所示的二叉树

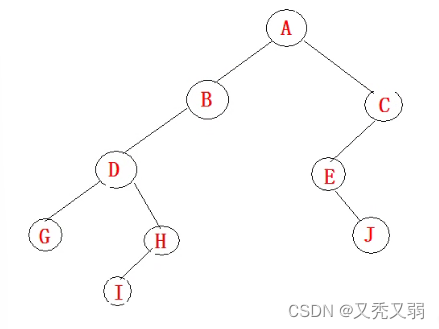
        第五次遇到*： * *，形成如下图所示的二叉树

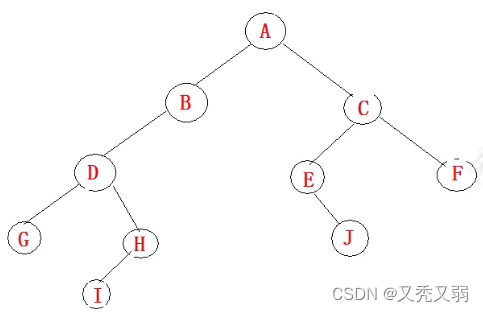
• 代码：

typedef struct node
{
    char value;//当前节点值
    struct node* left;//指向当前节点左孩子指针
    struct node* right;//指向当前节点右孩子指针
}Node;
 
 
//根据先序遍历创建二叉树
Node* Create(const char*& str) //因为要修改字符串就加了引用&
{
    if (*str == '*')
        return NULL;
    else
    {
        Node* newnode = (Node*)malloc(sizeof(Node));
        if (newnode != NULL)
        {
            newnode->value = *str;
            newnode->left = Create(++str);
            newnode->right = Create(++str);
            return newnode;
        }
    }
}

• 完整代码：

typedef struct node
{
    char value;//当前节点值
    struct node* left;//指向当前节点左孩子指针
    struct node* right;//指向当前节点右孩子指针
}Node;
 
typedef struct tree
{
    Node* root;
}Tree;
 
void InitTree(Tree* t)
{
    t->root = NULL;
}
 
//先序遍历创建二叉树
Node* Create(const char*& str) //因为要修改字符串就加了引用&
{
    if (*str == '*')
        return NULL;
    else
    {
        Node* newnode = (Node*)malloc(sizeof(Node));
        if (newnode != NULL)
        {
            newnode->value = *str;
            newnode->left = Create(++str);
            newnode->right = Create(++str);
            return newnode;
        }
    }
}
 
//递归实现先序遍历输出二叉树
void PreOrder(node* root)
{
    if (root != NULL)
    {
        printf("%c", root->value);
        PreOrder(root->left);
        PreOrder(root->right);
    }
}
//递归实现后序遍历输出二叉树
void PostOrder(node* root)
{
    if (root != NULL)
    {
        PostOrder(root->left);
        PostOrder(root->right);
        printf("%c", root->value);
    }
}
//递归实现中序遍历输出二叉树
void InOrder(node* root)
{
    if (root != NULL)
    {
        InOrder(root->left);
        printf("%c", root->value);
        InOrder(root->right);
    }
}
 
 
int main()
{
    Tree t;
    InitTree(&t);
    const char* str = "ABDG**HI****CE*J**F**";
    t.root = Create(str);
    printf("\n");
    printf("先序遍历二叉树：\n");
    PreOrder(t.root);
    printf("\n");
    printf("中序遍历二叉树：\n");
    InOrder(t.root);
    printf("\n");
    printf("后序遍历二叉树：\n");
    PostOrder(t.root);
    printf("\n");
}

• 运行结果：