二分法 二分搜索_二分搜索法和二分法的区别

1.引入：

        二分法的实质相当于简化的遍历，并将复杂度从n降低为log(n)，极其适用于大数据范围的筛选数据。

2.原理;

        二分法比较像数学中的介值定理，通过一次次较大范围的测试去确定范围。

        首先，在取值范围内的中间取值，判断是否是答案。如果不是，那判断是比所需答案大还是比所需答案小，然后根据大小关系改变取值一条边界的值。

        最后，直到收缩到左右边界相遇，二分结束，答案得出。

3.难点：

        二分的易错点主要有五个：

        (1) . 开始时，左右边界设置错误（牢记取中间值时，最终结果不是四舍五入，而是去尾）

        (2) . 改变边界位置时，新左右边界位置出错

        (3) . 结束条件出错

        (4) . 中间值计算位置导致少算一次（具体例子见下面错误示范）

        (5) . 二分时，数据必须递增或递减

4.二分模板：

        a.定义左 值 left 与第一个元素（或最小数据） 相等，右 值right比最后一个元素（或最大数据）大1；

        b.定义mid=(left+right）;

        c.开始while循环，结束条件是left+1==right;

        d.判断mid与答案大小关系，如果答案在mid左侧，令right=mid   ；   如果答案在mid右边，令left=mid；

        e.计算新的mid=(left+right)/2;  (一定要再计算一步，否则就会少算一次mid，导致出错)

5.相关查找函数：

        运用二分寻找数字位置时有lower_bound ; upper_bound ; binary_search;

        设一个数组a[100] .

        (1) . lower_bound表示搜索元素的第一个出现位置：

               格式：lower_bound(a+N,a+n,x)-a;         ------>输出a[N]到a[n]中x的第一个位置

lower_bound(a+N,a+n,x)-a;

        (2) . upper_bound表示搜索元素的最后一个出现位置：

               格式：upper_bound(a+N,a+n,x)-a;         ------>输出搜索从a[N]到a[n]中x的最后一个位置

upper_bound(a+N,a+n,x)-a;

        (3) . binary_search用来检测是否有所搜索元素：

                格式：binary_bound(a+N,a+n,x);          ------->bool型，输出true或false,判断a[N]到a[n]是否有x

binary_search(a+N,a+n,x);

6.例题：

（1）.

 

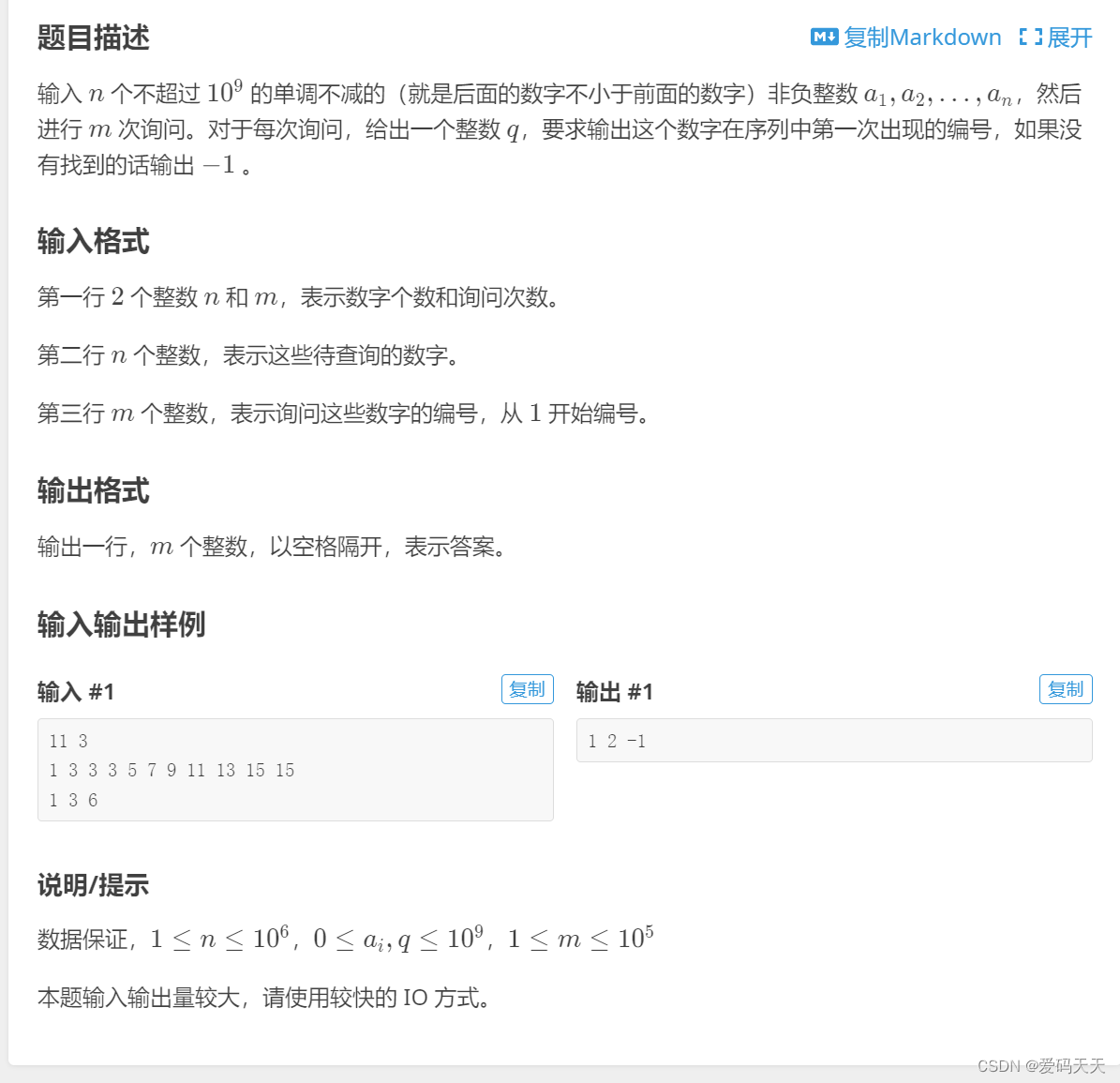
#include<iostream>
#include<algorithm>
using namespace std;
int a[100000009];
int main(){
	int N,n,goal;
	cin>>N>>n;
	for(int i=0;i<N;i++){
		cin>>a[i];
	}
	for(int i=0;i<n;i++){
		cin>>goal;
		int ans=lower_bound(a,a+N,goal)-a;
		if(a[ans]==goal)
 
判断是否有该元素
 
		cout<<ans+1<<" ";
		else
		cout<<-1<<" ";
	}
	return 0;
 } 

 在判断是否有所需元素时，通过判断lower_bound的值是否正确就可以判断是否不含这个元素。

但更好的方法是使用binary_search 

（2）.

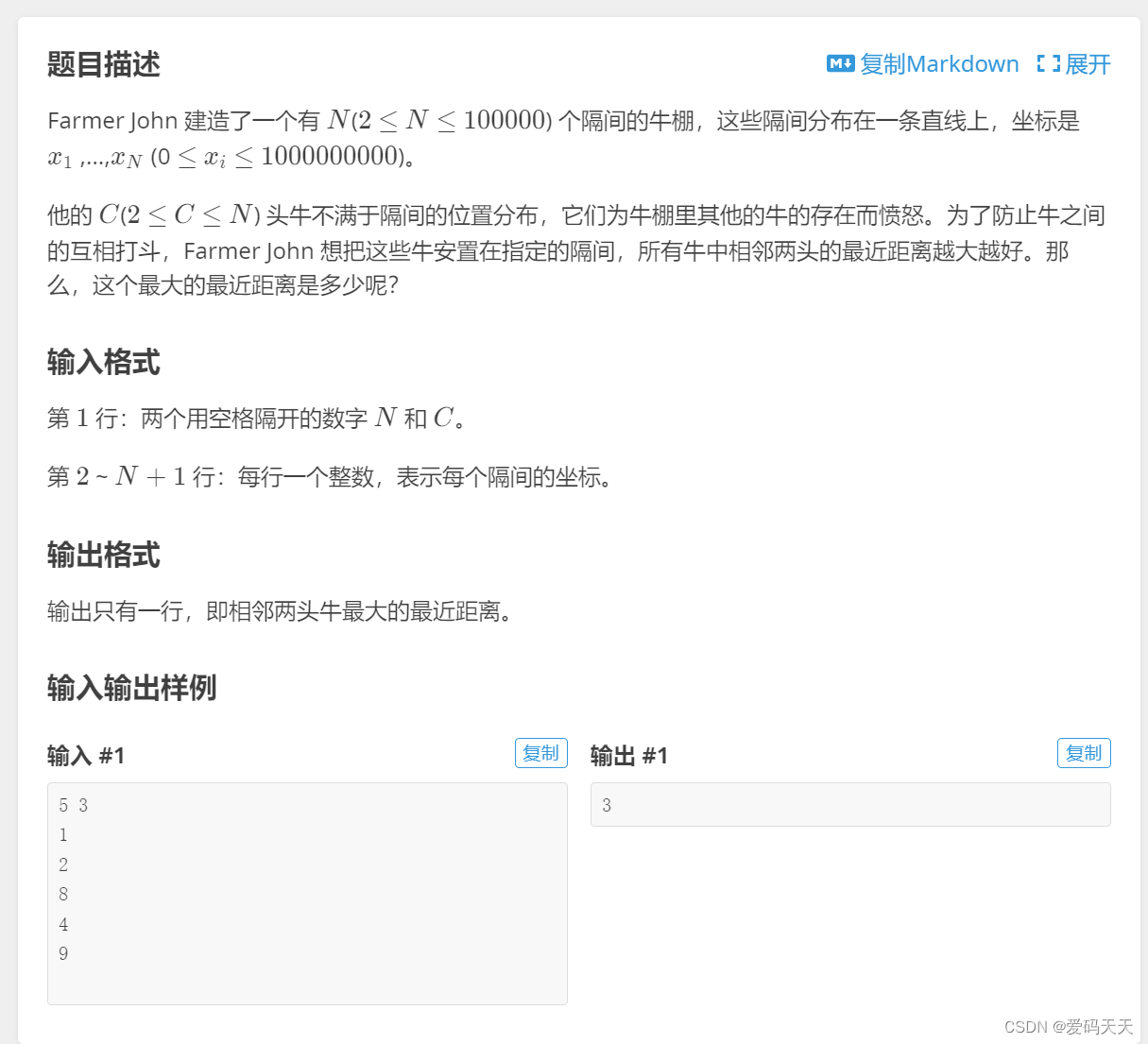
#include<iostream>
#include<algorithm>
using namespace std;
 
int n,N,a[100000005],num,mid;
 
bool check(int x){
	int first=a[0],num=1;
	for(int i=1;i<n;i++){
		if(a[i]-first>=x){
			num++;
			first=a[i];
 
//如果a[i]点放奶牛，将first值改变为该点
		
        }
	}
	if(num>=N) return true;
 
//判断是否能够放下所有奶牛
 
	else return false;
}
 
int main(){
	cin>>n>>N;
	for(int i=0;i<n;i++){
		cin>>a[i];
	}
	sort(a,a+n);
	int left=-1,right;
	right=a[n-1]+1;
	while(left!=right-1){
 
 
 
 
            mid=(left+right)/2;
 
 
 
 
			if(check(mid)) left=mid;
			else right=mid;	
	}
	cout<<mid;
	return 0;
} 

这是笔者第一次的错误算法，原因在于下方被隔开的那行有问题，因为在每次循环开始进行mid计算，就导致如果正确答案就是left的值时，输出值比标答大1。

因为最后一次改变的是：right = mid

mid设值标准方法：

 
	int left=-1,right;
	right=a[n-1]+1;
	mid=(left+right)/2;
	while(left!=right-1){
			if(check(mid)) left=mid;
			else right=mid;	
			mid=(left+right)/2;
	}
	cout<<mid;
	return 0;
} 

先进行mid赋值，再在每次while循环后计算mid。这样就避免了答案是left的情况。

以上为二分法的基本解释，如有错误，欢迎评论。