对线性插值的理解_渐性线性差值

【插值】

插值是用已知点求未知点的一种方法，而且通常是用两个已知点求一个未知点。（如果是用很多已知点求未知点一般用曲线拟合）

既然是用两个已知点求一个未知点，那么两个已知点之间的距离要尽可能的小，这样求出来的未知点才会尽可能的准确。

之所以用“已知点”而不用“已知值”是因为，已知点可以是用一个值表示的一维点，也可以是两个值表示的二位点，也可以是三个值表示的三维点。

什么叫两个一直点的距离要尽可能的小，这要看具体情况

如果A= 1，B= 100，单位都是m，在城市地图的情况下，还比较大；在国家地图的情况下，两个点距离非常小。

【线性插值】

如果是在两个点之间有一个未知点，如果我们不知道两个点之间的点怎么变化，我们通常认为是线性变化的，也即对两个点进行线性插值，得到第三个点。

线性插值的方法如下：

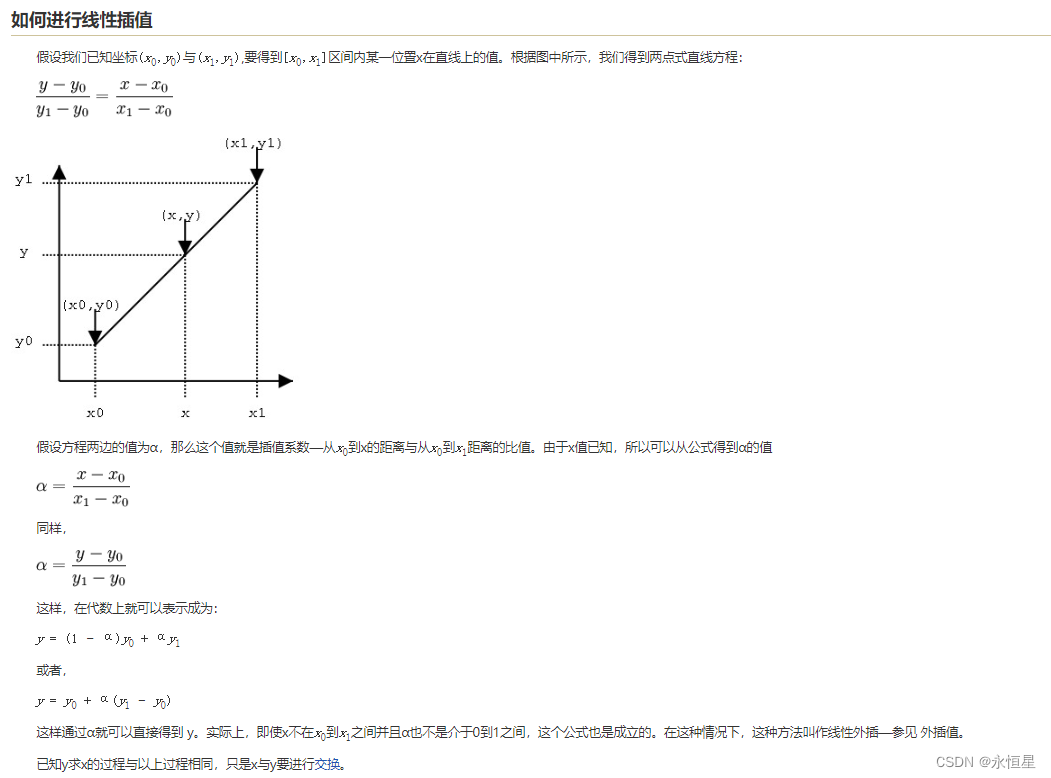
 可以直接将插值系数视为一个权重系数，取值范围在0到1之间。

【线性插值的不同用法】

不管在什么用法下，公式中的Y值都可以不是一个值，Y可以是一个二维坐标、三维坐标、一个向量、一个矩阵，甚至是一张图片，一个视频，一组数据等等。

1.只需要给个插值系数

有时候我们对具体的X并不关心，这种情况下，我们不需要知道x0、x1，只要有y0、y1，给插值系数取任何一个合适的值就可以。

2. 需要知道具体的X

在有些问题下，需要具体的x，给定具体的X后，相当于确定了一个具体的插值系数。一般这种问题会比较明显。

3.用线性插值做线性变化

这要求用线性插值在两个点之间算出一系列未知点，只要使得插值系数线性变化即可，例如0.1、0.2、0.3、0.4等等。

4.用线性插值做非线性变化

这要求用线性插值在两个点之间算出一系列未知点，只要使得插值系数线性变化即可，例如0.01、0.1、0.22、0.56等等。

5.用线性插值做线性逼近

保持插值参数不变，每次用插值出现的点当作新的y0，逼近y1

6.用线性插值做非线性逼近

非线性改变插值参数