Python调用MindOpt求解二次规划问题的几点总结_python 二次规划求解器

简介

本篇文章是系列文章的第三篇，MindOpt对于python的支持还是挺不错的，我已经编写了建模优化线性规划和混合整数线性规划问题的例子，下文我会对Python调用MindOpt建模优化二次规划问题进行总结。

如何获取MindOpt求解器

求解器安装包的发布渠道。请大家:

1. 前往 https://www.aliyun.com/product/ai/opt 来下载求解器软件。
2. 在阿里云上获取免费授权码:
   • 请大家迁移到“云鉴权”自助申请licenseKey，配置fl_client.ini。新的“云鉴权”不需要绑定机器ID，只要阿里云账号并联网就好。
   关于求解器的使用文档，请参考：https://help.aliyun.com/document_detail/298219.htm

二次规划定义

在前文线性规划问题示例中，讲述到线性规划在我个人认为是在线性的目标和约束中，找出一个最优解。而本文的二次规划，是非线性规划中的一类。具体地说，是一个线性约束的、二次规划问题，就是优化（最小化或最大化）二次函数目标的问题。

关于优化的类别，有很多，比如MindOpt的案例广场的标签里面提到的问题标签，就列出了常见的数学规划的类型。其中关于变量、约束、目标这建模三要素，进行罗列：

• 关于变量：取值有连续的，有整数的，还有更特殊的二进制（0或1）的，
• 关于约束和目标：一般用变量的函数变换来表达，其中约束再增加它函数的取值范围。
  • 当函数是变量的线性关系时，比如x的1次方相加，我们称呼为线性约束、线性的目标。（如果变量也是连续的，这个就是线性规划问题啦。）
  • 当函数是变量的是二次关系的时候，比如函数中有 x的2次方项。我们称呼为二次约束，或二次目标。
  • 函数还会有凸函数和非凸函数，数学里面都代表不同的特性，大家可以再多去查阅材料。

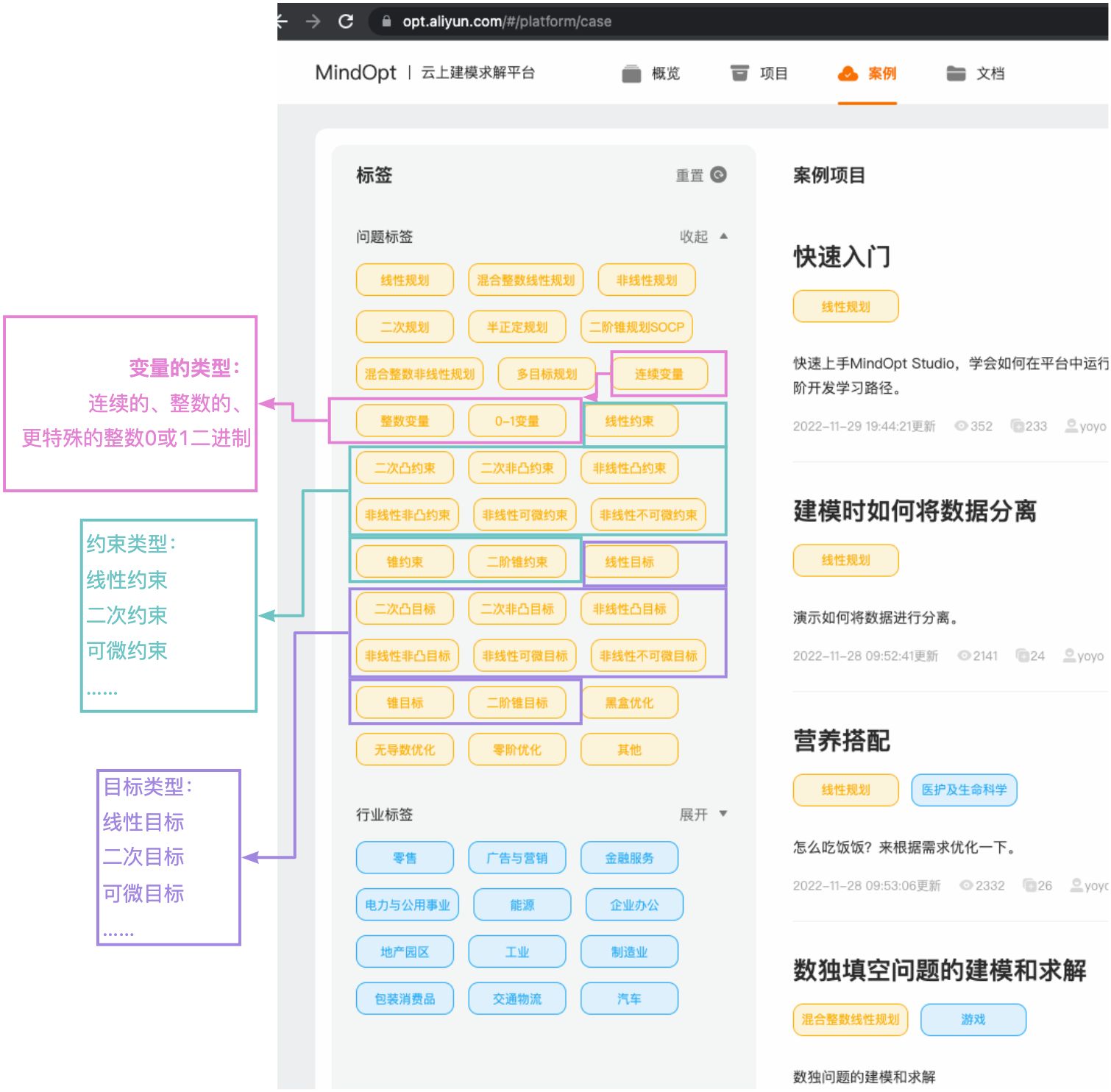
本文主要讲 凸二次规划，Convex Quadratic Programming。

二次规划问题：

"""
/**
 *  Description
 *  -----------
 *
 *  Linear optimization (row-wise input).
 *
 *  Formulation
 *  -----------
 *
 *  Minimize
 *    obj: 1 x0 + 1 x1 + 1 x2 + 1 x3
 *         + 1/2 [ x0^2 + x1^2 + x2^2 + x3^2 + x0 x1]
 *  Subject To
 *   c1 : 1 x0 + 1 x1 + 2 x2 + 3 x3 >= 1
 *   c2 : 1 x0 - 1 x2 + 6 x3 = 1
 *  Bounds
 *    0 <= x0 <= 10
 *    0 <= x1
 *    0 <= x2
 *    0 <= x3
 *  End
 */
"""
from mindoptpy import *


if __name__ == "__main__":

    MDO_INFINITY = MdoModel.get_infinity()

    # Step 1. Create a model and change the parameters.
    model = MdoModel()

    try:
        # Step 2. Input model.
        # Change to minimization problem.
        model.set_int_attr(MDO_INT_ATTR.MIN_SENSE, 1)
        
        # Add variables.
        x = []
        x.append(model.add_var(0.0,         10.0, 1.0, None, "x0", False))
        x.append(model.add_var(0.0, MDO_INFINITY, 1.0, None, "x1", False))
        x.append(model.add_var(0.0, MDO_INFINITY, 1.0, None, "x2", False))
        x.append(model.add_var(0.0, MDO_INFINITY, 1.0, None, "x3", False))

        # Add constraints.
        # Note that the nonzero elements are inputted in a row-wise order here.
        model.add_cons(1.0, MDO_INFINITY, 1.0 * x[0] + 1.0 * x[1] + 2.0 * x[2] + 3.0 * x[3], "c0")
        model.add_cons(1.0,          1.0, 1.0 * x[0]              - 1.0 * x[2] + 6.0 * x[3], "c1")

        # Add quadratic objective matrix Q.
        #
        #  Note.
        #  1. The objective function is defined as c^Tx + 1/2 x^TQx, where Q is stored with coordinate format.
        #  2. Q will be scaled by 1/2 internally.
        #  3. To ensure the symmetricity of Q, user needs to input only the lower triangular part.
        #
        # Q = [ 1.0  0.5  0    0   ]
        #     [ 0.5  1.0  0    0   ]
        #     [ 0.0  0.0  1.0  0   ]
        #     [ 0    0    0    1.0 ]
        model.set_quadratic_elements([ x[0], x[1], x[1], x[2], x[3] ], [ x[0], x[0], x[1], x[2], x[3] ], [  1.0,  0.5,  1.0,  1.0,  1.0 ])

        # Step 3. Solve the problem and populate the result.
        model.solve_prob()
        model.display_results()

    except MdoError as e:
        print("Received Mindopt exception.")
        print(" - Code          : {}".format(e.code))
        print(" - Reason        : {}".format(e.message))
    except Exception as e:
        print("Received exception.")
        print(" - Reason        : {}".format(e))
    finally:
        # Step 4. Free the model.
        model.free_mdl()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78

总结

1.创建模型

• 创建一个空的模型

model = MdoModel()
1

2.定义目标函数

• 利用Python API mindoptpy.MdoModel.set_int_attr() 将目标函数改为最小化
• 也可以选择这个模型属性model.set_int_attr(“MinSense”, 1) 数字1代表最小化，0代表最大化
• (MDO_INT_ATTR.MIN_SENSE, 1)和(“MinSense”, 1)的含义是一样的

model.set_int_attr(MDO_INT_ATTR.MIN_SENSE, 1)
1

3.定义求解变量

• mindoptpy.MdoModel.add_var()此函数可向模型引入一个新的变量，()里可以添加四个优化变量，定义其下界、上界、名称和类型
• 0.0是新增变量的下界，10和MDO_INFINITY是上界，没有值可以用无穷大来表示即MDO_INFINITY
• 1.0为新变量的目标系数
• None是包含非零元素的列对象，默认为None
• ""中是变量的名字，False代表不可指定是否为整数变量的布尔标志

x = []
x.append(model.add_var(0.0,         10.0, 1.0, None, "x0", False))
x.append(model.add_var(0.0, MDO_INFINITY, 1.0, None, "x1", False))
x.append(model.add_var(0.0, MDO_INFINITY, 1.0, None, "x2", False))
x.append(model.add_var(0.0, MDO_INFINITY, 1.0, None, "x3", False))
1
2
3
4
5

4.定义约束条件

• mindooptpy.MdoModel.add_cons()此函数可向模型引入一个新的约束，()里可以输入约束的左右侧值，以及表达式
• 1.0为新约束的左侧值，或临时线性对象。
• MDO_INFINITY和10为新约束的右侧值，或者一个约束名称的字符串
• "c0、c1"为这条约束的名字

model.add_cons(1.0, MDO_INFINITY, 1.0 * x[0] + 1.0 * x[1] + 2.0 * x[2] + 3.0 * x[3], "c0")
model.add_cons(1.0,          1.0, 1.0 * x[0]              - 1.0 * x[2] + 6.0 * x[3], "c1")
1
2

5.设置目标的二次项系数

• mindoptpy.MdoModel.set_quadratic_elements()此函数会修改二次规划的二次项矩阵中所有指定元素的值
• 前两组输入向量分别表示二次项中所有非零项的两个变量的索引
• 最后一组输入向量是与之相对应的非零系数值
• 为了确保 Q 的对称性，用户只需要输入其下三角形部分，并且在求解器内部会乘以 1/2

# Add quadratic objective matrix Q.
#
#  Note.
#  1. The objective function is defined as c^Tx + 1/2 x^TQx, where Q is stored with coordinate format.
#  2. Q will be scaled by 1/2 internally.
#  3. To ensure the symmetricity of Q, user needs to input only the lower triangular part.
#
# Q = [ 1.0  0.5  0    0   ]
#     [ 0.5  1.0  0    0   ]
#     [ 0.0  0.0  1.0  0   ]
#     [ 0    0    0    1.0 ]
model.set_quadratic_elements([ x[0], x[1], x[1], x[2], x[3] ], [ x[0], x[0], x[1], x[2], x[3] ], [  1.0,  0.5,  1.0,  1.0,  1.0 ])
1
2
3
4
5
6
7
8
9
10
11
12

6.设置参数：

可以通过mindooptpy.MdoModel.set_real_param()设置，例如设置求解时间上限等：

model.set_real_param("MaxTime", 7200.0)
# MindOpt 当前使用墙上时间作为默认计时。
# 如果将该值设置为0，则不会施加求解时间限制。
1
2
3

设置求解方法：

model.set_int_param("Method", 2) # 内点法
model.set_int_param("Method", 1) # 对偶单纯形法
model.set_int_param("Method", 0) # 原始单纯形法
model.set_int_param("Method", -1) # 让求解器决定(并发优化)
model.set_int_param("Method", -2) # 使用多线程单纯形法
1
2
3
4
5

更多可选参数使用方法

7.求解QP模型

• 模型输入后，我们接着用mindoptpy.MdoModel.solve_prob()来求解问题。
• 并用mindoptpy.MdoModel.display_results()呈现求解结果。

model.solve_prob()
model.display_results()
1
2

更多Python 接口函数使用方式
MindOpt最新版本1.1.1支持更多API、语法更简洁
下载地址、API查询地址

联系我们

钉钉群号：32451444
邮箱地址：solver.damo@list.alibaba-inc.com
更多更新通知：https://solver.damo.alibaba.com