数据结构与算法：红黑树

目录

什么是红黑树 

​编辑

红黑树的性质

红黑树的辨析

红黑树实现

红黑树的结构

红黑树的插入

 红黑树的调试

红黑树平衡判断

什么是红黑树 

这里引入一下NIL节点的概念：

NIL节点也称为空节点或外部节点，是红黑树中一种特殊的节点类型。NIL节点不存储实际的数据，它们的作用是协助维护红黑树的结构和性质，同时也简化了一些操作的实现。在红黑树中，每个节点要么是红色的，要么是黑色的，而每个节点都有左子节点和右子节点。NIL节点是所有叶子节点的虚拟父节点，它们都是黑色的，且不包含任何子节点。这意味着，如果一个节点没有左子节点或右子节点，那么它的对应子节点就是一个NIL节点。通过将红黑树的所有叶子节点都替换为NIL节点，我们可以保证红黑树的每个节点都至少有一个子节点。这样，我们就可以通过判断节点的子节点是否为NIL节点来处理边界情况，避免了在处理节点时需要特殊处理叶子节点的情况。 

红黑树的性质

因此我们在设计红黑树结构时，根节点特殊设置为BLACK，新增节点默认构造为RED 

因为插入一个新的黑色节点，就需要在所有路径中都要新增一个黑色节点，实现十分困难，就算能实现，也消耗巨大。 

红黑树的辨析

如上图：红黑树的5个性质

对于图一：我们需要辨析，没有红节点，一定不是红黑树吗？我们看性质1，就知道图1也满足红黑树的要求

对于图二：我们如果画出红色节点的NIL节点，会发现这条路径仅有2个黑色节点，而其他路径为3个黑色节点，黑色节点数目不同，所以不是红黑树 。

 所以我们知道了，判断红黑树时需要借助NIL节点来判断。

红黑树实现

红黑树的结构

回到第一张图片：红黑树是一种搜索二叉树，那么总体上的结构也是 树 和 树的节点，不同的是借助枚举类型来实现红黑的颜色

// 实现颜色
enum Colour
{
	RED,
	BLACK
};
 
template<class K, class V>
struct RBTreeNode {
	// 三叉链结构
	RBTreeNode<K, V>* _left;
	RBTreeNode<K, V>* _right;
	RBTreeNode<K, V>* _parent;
	// 键值对
	pair<K, V> _kv;
	// 实现颜色
	Colour _col;
 
	RBTreeNode(const pair<K, V>& kv)
		: _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _kv(kv)
		,_col(RED) // 默认新节点红色 根节点为黑
	{}
};
template<class K, class V>
class RBTree {
 
	typedef RBTreeNode<K, V> Node;
 
public:
 
 
private:
	Node* _root = nullptr;
};

红黑树的插入

基础的插入还是：判断key的值然后新建节点插入

	bool insert(const pair<K, V>& kv) {
 
		if (_root == nullptr) {
 
			_root = new Node(kv);
			// 根节点默认为黑色
			_root->_col = BLACK;
			return true;
		}
 
		Node* parent = nullptr;
		Node* current = _root;
 
		while (current != nullptr) {
 
			parent = current;
 
			if (current->_kv.first < kv.first)
				current = current->_right;
			else if (current->_kv.first > kv.first)
				current = current->_left;
			else
				return false;
		}
 
		current = new Node(kv);
        // 插入节点默认为红色
        current->_col = RED;
		// 通过大小插入左右
		if (parent->_kv.first < kv.first)
			parent->_right = current;
		else
			parent->_left = current;
 
		current->_parent = parent;
		
 
		// 实现颜色的变换
 
 
		return true;
	}

接着我们开始分析红黑树的插入情况！

注意一点：在红黑树中，不能随便增加黑色节点，因为假设在某一局部子树中增加黑色节点，其他部分子树的黑色节点可能会少于这一条路径

情况一：不用变色，完美符合红黑树性质，不用旋转，保持较好平衡

这里我们可以看出当插入节点的parent为黑色的时候，插入节点不需要进行变色，因为插入节点默认为红色，只要父节点不为红色就不用调整颜色，如果为红色就不符合性质

情况二：需要变色，插入不符合红黑树性质，不用旋转，保持较好平衡

这里呼应了情况一：插入节点的父节点为红色，需要变色，这里实现结束把父节点改成黑色，把祖父节点改为红色，把祖父节点的另一个子节点也改为黑色，说到这里大概就知道怎么实现了，我们先不着急，先继续研究

总结一下：仅变色时的一般规律 

注意这里的抽象图带有a，b，c，d，e这些可能是带有一个黑色节点的子树。并且current不一定是新增节点，也有可能是调整后的节点。我们在后面会有讲解

这里我们开始引入Node* uncle节点来辅助我们分析 

 如果祖父节点的父节点为黑色，那么不用调整。当祖父节点的父亲为红色节点，需要将新的current = grandparent来向上继续调整！

稍微演示一下：

这里最终头上红色节点也可能需要向上调整！

情况三：需要变色 并且需要 旋转

(1) 当current = parent->_left

这里我们看出来，如果仅仅靠着变色还是无法解决问题，而是需要通过变色后来判断是否需转。红黑树判断旋转的方式是通过比较插入节点的祖父节点、父节点和插入节点的位置关系，来确定需要进行的旋转操作。

对于AVL树来说，通过每个节点上的平衡因子来研究是否需要旋转。

u存在且为黑过程

(2) 当current = parent->_right

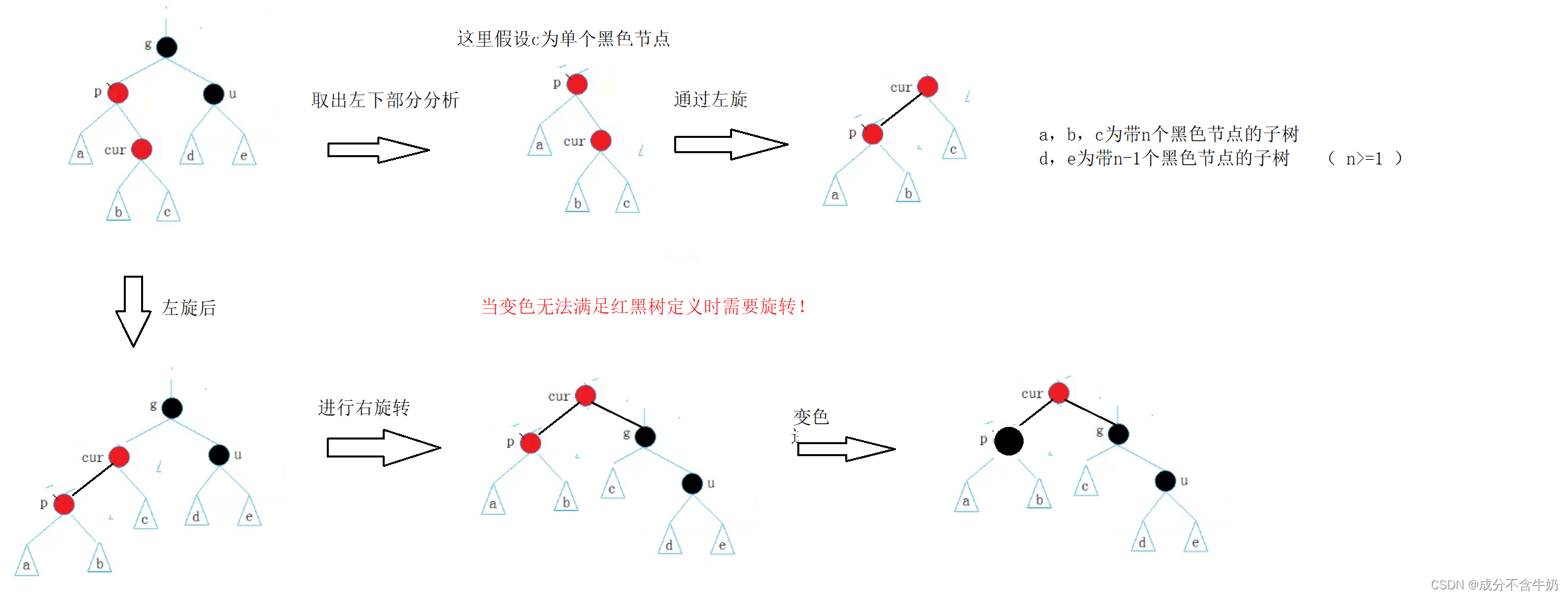
特殊情况：这里大家假设a，b，c为一个黑色节点，d，e为一个红色节点来分析画图。

回顾一下红黑树旋转的情况，我们如何在代码中体现：

1.首先我们在通过上述分析时发现，当变色无法变为红黑树的时候，就需要旋转一下才能通过变色成为红黑树

2.其次我们也总结出了：当current和parent均为红色，uncle不存在或者是为黑色的情况就需要进行旋转和变色

3.这里current的位置可以在parent的左或者右，这里就需要分成两种，再接着uncle可能在grandparent的左或者右，又是两种，所以需要分为if else 嵌套if else

4.最终我们完成旋转和变色

这一部分要注意current不一定是新增节点！

current可能是插入节点经过调整后的grandparent，或者是不断调整后的ggggggrandparent

 那么代码大致我们就可以写出来了，旋转部分的代码这里有具体讲解数据结构与算法：AVL树-CSDN博客

	bool insert(const pair<K, V>& kv) 
	{
 
		// 1.先插入节点
 
		if (_root == nullptr) 
		{
			_root = new Node(kv);
			// 根节点默认为黑色
			_root->_col = BLACK;
			return true;
		}
 
		Node* parent = nullptr;
		Node* current = _root;
 
		while (current != nullptr) 
		{
 
			parent = current;
 
			if (current->_kv.first < kv.first)
				current = current->_right;
			else if (current->_kv.first > kv.first)
				current = current->_left;
			else
				return false;
		}
 
		current = new Node(kv);
		// 新增节点默认为红色
		current->_col = RED;
 
		// 通过大小插入左右
		if (parent->_kv.first < kv.first)
			parent->_right = current;
		else
			parent->_left = current;
 
		current->_parent = parent;
		
	
		// 2.实现颜色的变换  情况来回的迭代直至不满足循环 退出时就满足了红黑树
		while (parent != nullptr && parent->_col == RED)
		{
			/*进入循环情况：同时满足父节点不为空，且为红色
			  原因： 如果父节点为空，则current为_root
			        如果父节点为黑色，就不用更新颜色了*/
 
			Node* grandparent = parent->_parent;
			
			// 找到叔叔节点位置
			if (parent == grandparent->_left)
			{
				// uncle在父亲右边
				Node* uncle = grandparent->_right;
 
				// 情况一：叔叔存在，且叔叔为红色
				if (uncle != nullptr && uncle->_col == RED)
				{
					parent->_col = uncle->_col = BLACK;
					grandparent->_col = RED;
					// 继续向上调整
					current = grandparent;
					parent = current->_parent;
				}
				// 情况二：叔叔不存在 或者 叔叔存在但是颜色为黑色
				else
				{
					
					if (current == parent->_left)
					{
						RotateR(grandparent);
						parent->_col = BLACK;
						grandparent->_col = RED;
					}
					// current在右边
					else
					{
						RotateL(parent);
						RotateR(grandparent);
						// 通过旋转后，旋转内部就已经完成了指针的指向
						current->_col = BLACK;
						grandparent->_col = RED;
 
					}
					// 直接退出循环即可，也可以不退出，因为父亲已经为黑色了
					break;
				}
			}
				
			else 
			{
				// uncle在父亲左边
				Node* uncle = grandparent->_left;
				if (uncle != nullptr && uncle->_col == RED)
				{
					parent->_col = uncle->_col = BLACK;
					grandparent->_col = RED;
					// 继续向上调整
					current = grandparent;
					parent = current->_parent;
				}
				else 
				{
					if (current == parent->_right)
					{
						RotateL(grandparent);
						parent->_col = BLACK;
						grandparent->_col = RED;
					}
					// current在左边
					else {
						// 注意这里单旋的节点不同
						RotateR(parent);
						RotateL(grandparent);
						grandparent->_col = RED;
						current->_col = BLACK;
					}
 
					break;
				}
			}	
		}
		// 保持根节点始终为黑色，当current到达根节点可能为RED，这里就在外部变黑
		_root->_col = BLACK;
		return true;
	}
 
 
	// 左单旋
	void RotateL(Node* root)
	{
		Node* parent = root;
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		Node* grandparent = parent->_parent;
 
		subR->_left = parent;
		parent->_right = subRL;
 
		if (subRL != nullptr)
			subRL->_parent = parent;
 
		parent->_parent = subR;
		parent = subR;
 
		if (grandparent == nullptr)
		{
			_root = parent;
		}
		else 
		{
			if (grandparent->_left == root)
				grandparent->_left = parent;
			else
				grandparent->_right = parent;
		}
		parent->_parent = grandparent;
	
	}
	// 右单旋
	void RotateR(Node* root)
	{
		Node* parent = root;
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		Node* grandparent = parent->_parent;
 
		subL->_right = parent;
		parent->_left = subLR;
		
		if(subLR!=nullptr)
		{
			subLR->_parent = parent;
		}
		parent->_parent = subL;
		parent = subL;
 
		if (grandparent == nullptr)
		{
			_root = parent;
		}
		else
		{
			if (grandparent->_left == root)
				grandparent->_left = parent;
			else
				grandparent->_right = parent;
		}
		parent->_parent = grandparent;
 
	}

 红黑树的调试

说到调试，对比以往的学习来说，红黑树的测试比较困难，所以我们有必要来学习一下

先放个测试的代码

void test1() {
 
 
	RBTree<string, string> RB_tree;
 
	RB_tree.insert(make_pair("zhong", "2022044026"));
	RB_tree.insert(make_pair("Hello", "2022044026"));
	RB_tree.insert(make_pair("world", "2022044026"));
	RB_tree.insert(make_pair("C++", "2022044026"));
	RB_tree.insert(make_pair("CPP", "2022044026"));
	RB_tree.insert(make_pair("JAVA", "2022044026"));
	RB_tree.insert(make_pair("PYTHON", "2022044026"));
 
	RB_tree.inOrder();
}

通过调试中的监视图可以查看这棵树节点的红黑、相对地址 

同时我们可以把 string类型换为int类型来测试画图，放一个样例，大家可以试着画一下

void test2() {
 
	int arr[] = {16, 3, 7, 11, 9, 26, 18, 14, 15 };
	RBTree<int, int> RB_tree;
	for (auto& e : arr) {
 
		RB_tree.insert(make_pair(e, e));
		// cout << "insert: " << e << " -> " << RB_tree.ifBalance() << endl;
	}
	RB_tree.inOrder();
	cout << "是否平衡：" << RB_tree.ifBalance() << endl;
 
}

红黑树平衡判断

判断红黑树的平衡，我们首先知道红黑树的平衡与AVL树不同的是，红黑树实现的是相对平衡，从红黑树的性质来说，判断红黑树是否平衡，主要是满足红黑树的性质

1.根节点为黑色

2.每条路径的黑色节点数目一致

3.不存在连续的红色节点

 那么判断红黑树的平衡就有迹可循了！直接上代码了

	bool check(Node* root, int blackNum, const int flag)
	{
		if (root == nullptr) 
		{
			// cout << "黑色节点数目：" << blackNum << endl;
			
			if (blackNum != flag)
			{
				cout << "路径上的黑色节点数存在不同" << endl;
				return false;
			}
 
			return true;
		}
 
		if (root->_col == RED && root->_parent->_col == RED) 
		{
			// 子节点和父节点均为红色，不符合红黑树
			cout << "存在连续的红色节点" <<endl;
			return false;
		}
		if (root->_col == BLACK)
			++blackNum;
 
		// 传值调用，只影响函数块，上一层不影响下一层
		return check(root->_left, blackNum, flag) && check(root->_right, blackNum, flag);
	}
 
	// 判断是否平衡
	bool ifBalance()
	{
		if (_root == nullptr)
			return true;
 
		if (_root->_col == RED)
			return false;
		// 作为辅助判断
		int flag = 0;
		Node* current = _root;
 
		while (current != nullptr)
		{
			if (current->_col == BLACK)
				flag++;
			current = current->_left;
		}
		// 设置一个flag值记录某一条路径的长度
		// 如果flag不等于任何一条路径的长度就表示某一条路径黑色节点数有误
 
		cout << "flag大小为：" << flag << endl;
		// 根节点到当前节点路径上黑色节点数量
		int blackNum = 0;
		return check(_root, blackNum, flag);
	}

到了这里，我们初步学习了红黑树的原理