不正经

这个屌丝很懒，什么也没留下！

热门标签

一文通透想取代MLP的KAN：通俗理解Kolmogorov-Arnold定理和KAN的方方面面_kan mlp

作者：不正经 | 2024-05-29 05:21:22

踩

kan mlp

前言

24年5.19，我司七月的LLM论文100课里的一学员在课程q群内提到，“最近总是看到KAN，KAN这个概念重要吗？需要了解学习吗？”，我当时回复道：KAN值得学习和了解，咱们课程上也要讲一下

在讲之前，我也在本博客内好好梳理下，毕竟牵扯到KAN的概念很多，对于初学者而言，需要具备的背景知识则更多，所以本文的出发点是：

假定很多背景知识都不具备，是否可以通畅无比的理解KAN的方方面面，比如为何提出、从何发展而来、其网络架构是什么、与MLP的异同是什么，有何优势及局限等等
对于喜欢抠细节的，如果KAN论文中没有写清楚的很多细节、背景知识，到底有没有一篇文章足够详尽、足够细致的解释清楚KAN论文中所涉及的一切？

如此，本文也就出来了：可视为对此篇论文《KAN: Kolmogorov-Arnold Networks》的足够全面、详尽、细致的解读，且为了通透彻底、通俗易懂，一方面，我个人在原论文的基础上列举了大量的示例，二方面做了原论文中没有的大量的补充说明、解读(比如花了大量的篇幅和示例解释论文中的公式2.15)

同时，本文也算是见证我司新的使命的诞生

通过大模型帮助B端客户提升生产力的过程中，逐步打造世界级通用产品
通过博客、课程与广大同行(大模型开发者)共同进步，提升中国在大模型时代的竞争力

最后，如果某个公式你没有看的特别明白，没事，我可能已经感应到了，本文会不断完善，直到5月底，5月底之后，如还有不明白的，欢迎随时留言，我会根据留言情况再做针对性的说明解释

第一部分从MLP到Kolmogorov-Arnold Networks(KANs)

1.1 背景知识：Kolmogorov-Arnold表示定理与Basic Spline(基础样条)函数

1.1.1 Kolmogorov-Arnold表示定理：任意多变量连续函数可以表示为一系列单变量函数的组合

多层感知器(MLPs)[1, 2, 3]，也被称为全连接前馈神经网络(在节点“神经元”上具有固定的激活函数)，是当今深度学习模型的基础构建模块。作为机器学习中用于逼近非线性函数的默认模型，其由通用逼近定理来实现

然而，尽管MLPs被广泛使用，但它们存在显著缺点。例如，在transformers [4]中，MLPs几乎消耗了所有非嵌入参数，并且通常比较难以解释(相对于注意力层)，除非使用后续分析工具 [5]

因此，作者团队提出了一个替代方案，称为Kolmogorov-Arnold Networks(KANs)，与MLPs受到通用逼近定理的启发不同，KANs受到Kolmogorov-Arnold表示定理的启发 [6, 7]

那什么又是所谓的Kolmogorov-Arnold表示定理呢？

Vladimir Arnold(算是前苏联神通)和其导师Andrey Kolmogorov(前苏联科学院院士)证明，，如果 $f$ 是有界域上的多元连续函数(if f is a multivariate continuous function
on a bounded domain)，则 $f$ 可以写成有限个连续函数的复合单变量和加法的二元运算(then f can be written as a finite composition of continuous functions of a single variable and the binary operation of addition)

说白了，任意一个连续函数 $f\left(x_{1}, \ldots, x_{n}\right)$ 都可以表示为有限个单变量函数的嵌套组合(如下公式所示，其中 $\phi_{q, p}$ 、 $\Phi_{q}$ 都是单变量函数)
$f(x)=\sum_{q=1}^{2 n+1} \Phi_{q}\left(\sum_{p=1}^{n} \varphi_{q, p}\left(x_{p}\right)\right)$

好比我带队的我司审稿项目组在通过paper-review数据集微调一系列开源模型时，大家是各自并行微调各个开源模型(即各调各的，不用多个人同时微调同一个模型)，最终汇总所有人的结果

更具体地，对于一个光滑 $f:[0,1]^{n} \rightarrow \mathbb{R}$ ，如下所示(定义为公式2.1)

$f(\mathbf{x})=f\left(x_{1}, \cdots, x_{n}\right)=\sum_{q=1}^{2 n+1} \Phi_{q}\left(\sum_{p=1}^{n} \phi_{q, p}\left(x_{p}\right)\right)$

由于论文中没有细致指出每一个变量的含义，但考虑到本文追求的详尽、细致的缘故，故我补充解释一下，其中各个变量的含义
其中， $x_p$ 即代表向量 $x$ 的第 $p$ 个元素，故 $p$ 的范围是从1到 $n$ ( $n$ 是输入向量的维度)
$q$ 这个索引用于遍历外部函数 $\Phi$ 的每个组成部分
故有一元函数 $\phi_{q, p}$ (或称单变量函数)处理输入向量 $x$ 的第 $p$ 个分量，并为第 $q$ 个外部函数的求和贡献一个项

定理指出，你可以用 2n+1 个这样的外部函数——每个外部函数 $\Phi_{q}$ 是一个一元函数(它作用于由内部一元函数 $\phi_{q, p}$ 的输出组成的求和)，来表示任何多变量函数 $f$
总之，每个函数都可以用一元函数和求和来表示(since every other function can be written using univariate functions and sum)，看似前途一片光明，因为学习高维函数可以因此归结为学习多项式数量的一维函数(learning a high-dimensional function boils down to learning a polynomial number of 1D functions)
然而，这些一维函数可能是非光滑甚至是分形的，因此在实践中可能无法学习(However, these 1D functions can be non-smooth and even fractal, so they may not be learnable in practice)

1.1.2 表示平滑曲线的B-spline(B样条)函数：通过多个分段多项式拼接而成，每个分段多项式由一组控制点(网格点)定义

为方便更好的理解，特补充一个KAN论文中没有的背景知识，即所谓的样条函数

样条函数(spline function)是一种用于逼近或插值数据的平滑函数，它由分段多项式拼接而成，并且这些多项式在连接处具有一定的连续性(相当于通过分段多项式的组合，以在不牺牲光滑性的前提下精确地逼近或插值数据)

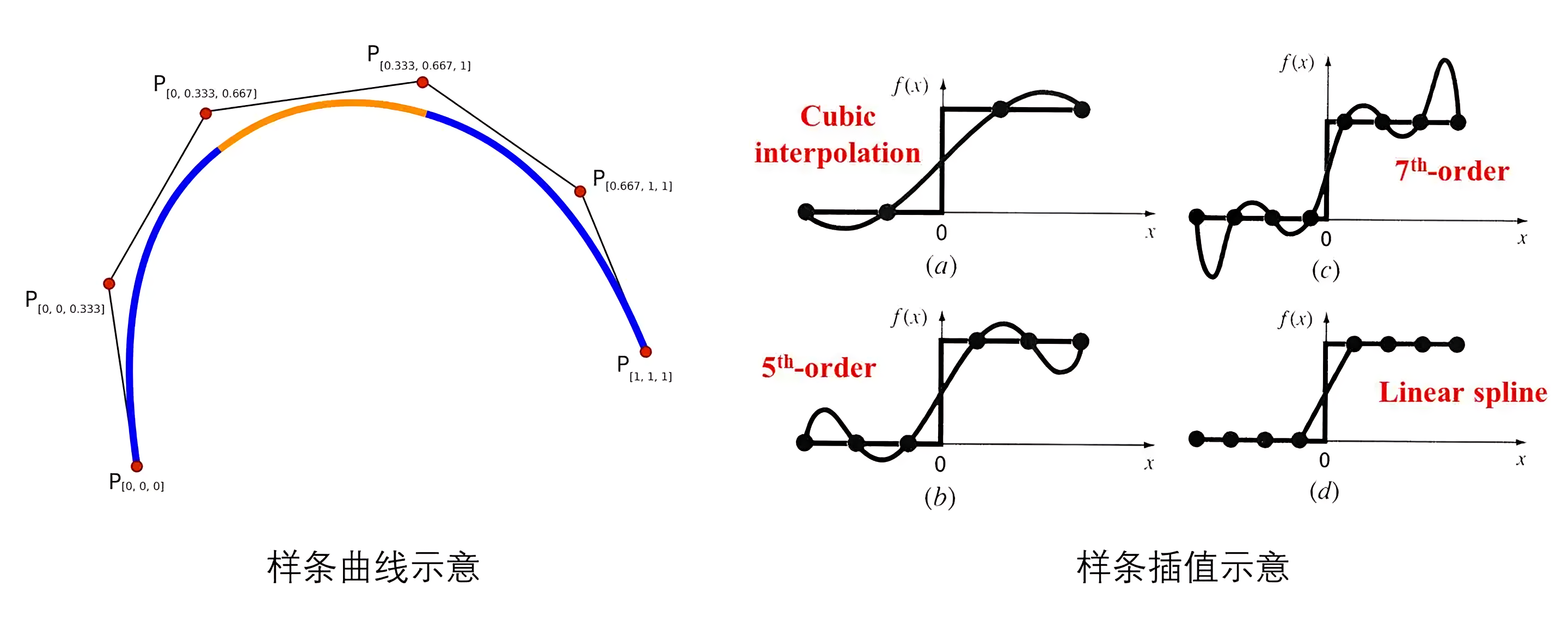
其分为

线性样条

二次样条

三次样条

B样条(B-spline)

每个子区间上使用一阶多项式，即直线段

它们在节点处具有零阶连续性，即函数值连续，但导数不连续

在每个子区间上使用二阶多项式

在节点处通常要求函数值和一阶导数连续

在每个子区间上使用三阶多项式

在节点处要求函数值、一阶导数和二阶导数都连续

使用一组基函数来表示样条。这些基函数具有局部支撑性，即每个基函数只在少数几个子区间上非零

对于B-spline，函数在其定义域内、在结点(Knot)都具有相同的连续性，其多项式表达可由Cox-de Boor递推公式表达

$\begin{aligned} B_{i, 0}(x) & :=\left\{\begin{array}{ll} 1 & \text { if } t_{i} \leq x<t_{i+1} \\ 0 & \text { otherwise. } \end{array}\right. \\ B_{i, k}(x) & :=\frac{x-t_{i}}{t_{i+k}-t_{i}} B_{i, k-1}(x)+\frac{t_{i+k+1}-x}{t_{i+k+1}-t_{i+1}} B_{i+1, k-1}(x) \end{aligned}$

可以应用于

插值(Interpolation)：即通过已知数据点来构造一条平滑曲线，以便在数据点之间进行估计
数据拟合(Data Fitting)：可以对大量噪声数据进行平滑处理，从而得到一个逼近数据的光滑函数
计算机图形学(Computer Graphics)：广泛用于图形和动画中，用于表示和控制复杂的曲线和曲面

1.2 KAN的发展起源：从何发展而来以及如何扩宽、扩深

1.2.1 KAN的提出是为了解决什么问题

进一步，如果我们面对一个由输入-输出对 $\left\{\mathbf{x}_{i}, y_{i}\right\}$ 组成的监督学习任务，则

我们需要找到 $f$ ，使得对所有数据点都有 $y_{i} \approx f\left(\mathbf{x}_{i}\right)$ ，从而只需找到适当的一元函数 $\phi_{q, p}$ 和 $\Phi_{q}$ 即可，由此而启发需要设计一个神经网络，以明确地参数化公式2.1
由于要学习的所有函数都是一元函数，故可以将每个一维函数参数化为B-spline曲线(注意，很多地方会把spline翻译成样条，即spline = 样条)，其中局部 B-spline基函数的可学习系数(见下图右侧)

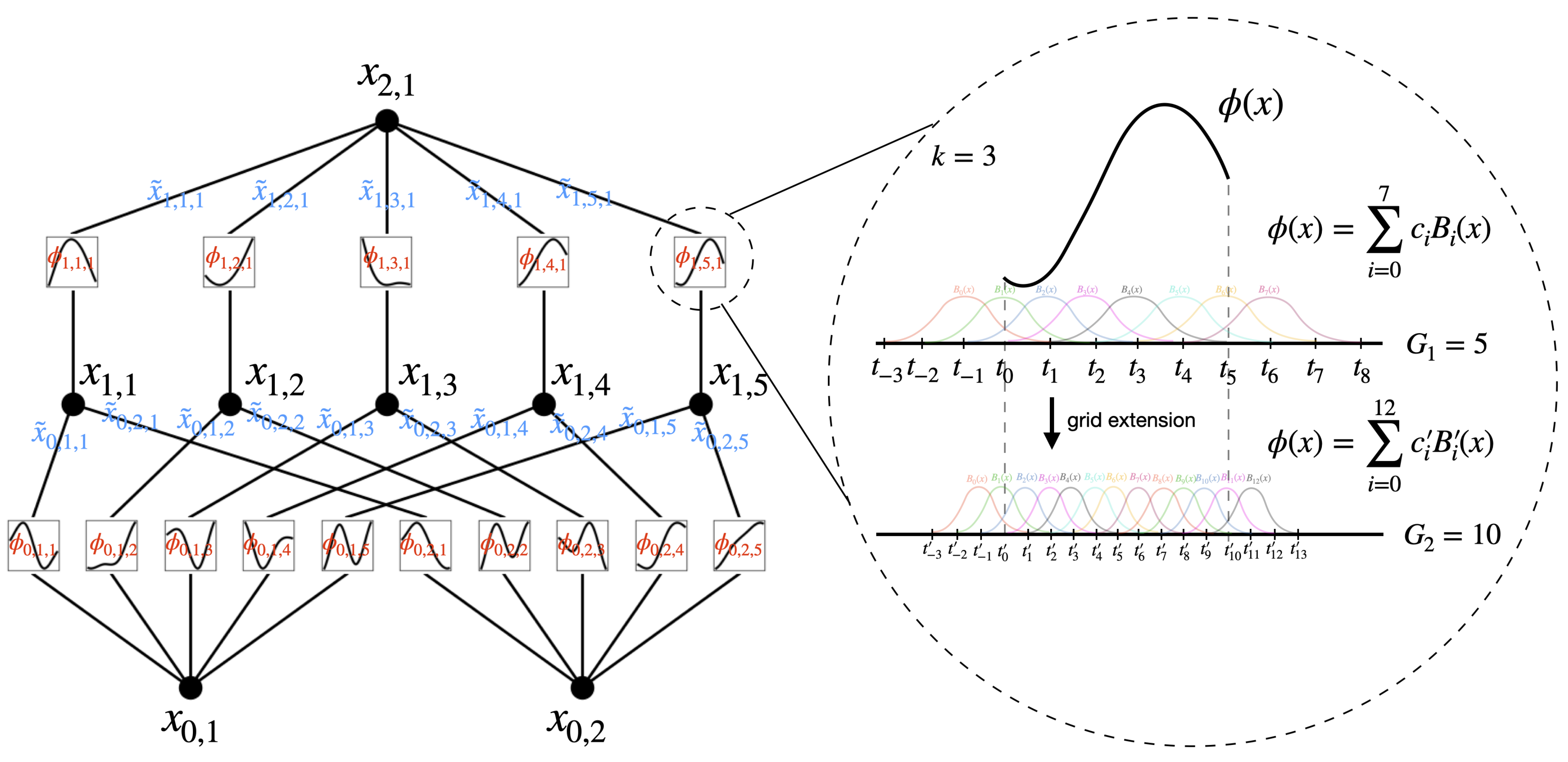
对于KAN而言，它通过B样条函数来参数化： $\phi_{q, p}$ 、 $\Phi_{q}$ 这些单变量函数，并通过组合这些函数来构建整个网络

so，现在我们有了 KAN 的原型，其计算图完全由方程式(2.1)指定，并在下图(b)中进行了说明

输入维度为 2，呈现为一个两层神经网络
激活函数放置在边edges上而不是节点nodes上(节点上执行简单求和)，中间层的宽度为2n+ 1

总之，在KAN之前，便有不少研究利用Kolmogorov-Arnold表示定理构建神经网络。然而，大多数工作仍停留在原始深度为2、宽度为2n+ 1的表示上「深度为2、宽度为2n+ 1，即2-Layer KAN with shape [n, 2n + 1, 1]」，并没有机会利用反向传播训练网络

KAN的贡献在于将原始Kolmogorov-Arnold表示扩展为任意宽度和深度，那具体如何扩展呢，请看下节

1.2.2 如何把KAN从2层2n+ 1宽推广到更深、更宽

在MLPs中，一旦我们定义了一个层(由线性变换和非线性组成)，便可以堆叠更多层使网络更深

类似的，要构建深层KANs，首先要回答：“什么是KAN层？” 原来，具有输入维度和输出维度的KAN层可以被定义为一维函数矩阵(定义为公式2.2)

$\boldsymbol{\Phi}=\left\{\phi_{q, p}\right\}, \quad p=1,2, \cdots, n_{\text {in }}, \quad q=1,2 \cdots, n_{\text {out }},$

其中函数 $\phi_{q, p}$ 具有可训练参数

在Kolmogorov-Arnold定理中，先“散”后“聚”
内部函数 $\phi_{q, p}$ 形成一个KAN层，其中输入维度 $n_{\text {in }}=n$ ，输出维度 $n_{\text {out }}=2 n+1$
这表明每个输入变量 $x_p$ 通过一组函数转换，输出的数量是输入数量的两倍加一，这样设计是为了充分捕获输入特征的信息并转化为中间表示
外部函数 $\Phi_{q}$ 形成一个KAN层，其中输入维度 $n_{\text {in }}=2 n+1$ ，输出维度 $n_{\text {out }}=1$
这层的功能是将内部函数层的所有输出整合起来，形成最终的模型输出

因此，方程2.1中的Kolmogorov-Arnold表示简单地由两个KAN层组成
$f(\mathbf{x})=f\left(x_{1}, \cdots, x_{n}\right)=\sum_{q=1}^{2 n+1} \Phi_{q}\left(\sum_{p=1}^{n} \phi_{q, p}\left(x_{p}\right)\right)$
现在清楚了什么是更深层的Kolmogorov-Arnold表示：简单地堆叠更多的KAN层

对于下图左侧而言，KAN的形状由整数数组表示： $\left[n_{0}, n_{1}, \cdots, n_{L}\right]$ ，再次引用上文的这个图以做说明

其中 $n_{i}$ 是计算图中第 $i$ 层节点的数量(比如当从0开始计数的话，上图第1层总计5个节点)
且用 $(l, i)$ 表示第 $l$ 层的第 $i$ 个神经元(比如上图 $x_{1,2}$ 表示第1层第2个神经元)
并用 $x_{l, i}$ 表示 $(l, i)$ -神经元的激活值
在第 $l$ 层和第 $l+ 1$ 层之间，有 $n_{l} n_{l+1}$ 激活函数(从第1层到第2层， $l = 1$ ，则总计有 $5\times 1$ 个激活函数)
连接 $(l, i)$ 和 $(l+ 1, j)$ 的激活函数用下述公式表示(比如 $\phi_{1, 1, 1}$ 、 $\phi_{1,2,1}$ 、 $\phi_{1, 3,1}$ 、 $\phi_{1, 4, 1}$ 、 $\phi_{1, 5,1}$ )
$\phi_{l, j, i}, \quad l=0, \cdots, L-1, \quad i=1, \cdots, n_{l}, \quad j=1, \cdots, n_{l+1}$
$\phi_{l, j, i}$ 的预激活简单地是 $x_{l, i}$ ，即 $x_{1,1}$ 、 $x_{1,2}$ 、 $x_{1,3}$ 、 $x_{1,4}$ 、 $x_{1,5}$
$\phi_{l, j, i}$ 的后激活用 $\tilde{x}_{l, j, i} \equiv \phi_{l, j, i}\left(x_{l, i}\right)$ 表示， $\tilde{x}_{1, 1, 1}$ 、 $\tilde{x}_{1, 2, 1}$ 、 $\tilde{x}_{1,3, 1}$ 、 $\tilde{x}_{1, 4, 1}$ 、 $\tilde{x}_{1, 5, 1}$
第 $(l+ 1, j)$ 神经元即 $x_{2,1}$ 的激活值简单地是所有传入后激活的总和(定义为公式2.5)
$x_{l+1, j}=\sum_{i=1}^{n_{l}} \tilde{x}_{l, j, i}=\sum_{i=1}^{n_{l}} \phi_{l, j, i}\left(x_{l, i}\right), \quad j=1, \cdots, n_{l+1}$
以矩阵形式表示，这可以写成(定义成公式2.6，注意，一列一列的竖着看)
$\mathbf{x}_{l+1}=\underbrace{\left(\begin{array}{cccc} \phi_{l, 1,1}(\cdot) & \phi_{l, 1,2}(\cdot) & \cdots & \phi_{l, 1, n_{l}}(\cdot) \\ \phi_{l, 2,1}(\cdot) & \phi_{l, 2,2}(\cdot) & \cdots & \phi_{l, 2, n_{l}}(\cdot) \\ \vdots & \vdots & & \vdots \\ \phi_{l, n_{l+1}, 1}(\cdot) & \phi_{l, n_{l+1}, 2}(\cdot) & \cdots & \phi_{l, n_{l+1}, n_{l}}(\cdot) \end{array}\right)}_{\boldsymbol{\Phi}_{l}} \mathbf{x}_{l},$
其中， $\boldsymbol{\Phi}_{l}$ 是对应于第 $l$ 层的函数矩阵(B-spline函数矩阵)，x为输入矩阵
一般的KAN网络是由 $L$ 层组成的：给定一个输入向量 $\mathbf{x}_{0} \in \mathbb{R}^{n_{0}}$ ，KAN的输出是(定义为公式2.7)
$\operatorname{KAN}(\mathbf{x})=\left(\boldsymbol{\Phi}_{L-1} \circ \boldsymbol{\Phi}_{L-2} \circ \cdots \circ \boldsymbol{\Phi}_{1} \circ \boldsymbol{\Phi}_{0}\right) \mathbf{x}$

最简的KAN则可以写为： $f(x)=\boldsymbol{\Phi}_{\text {out }} \circ \boldsymbol{\Phi}_{\text {in }} \circ \mathbf{x}$
还可以重写上述方程，使其更类似于方程2.1，假设输出维度 $n$ 为1，并定义 $f(\mathbf{x}) \equiv \operatorname{KAN}(\mathbf{x})$
$f(\mathbf{x})=\sum_{i_{L-1}=1}^{n_{L-1}} \phi_{L-1, i_{L}, i_{L-1}}\left(\sum_{i_{L-2}=1}^{n_{L-2}} \cdots\left(\sum_{i_{2}=1}^{n_{2}} \phi_{2, i_{3}, i_{2}}\left(\sum_{i_{1}=1}^{n_{1}} \phi_{1, i_{2}, i_{1}}\left(\sum_{i_{0}=1}^{n_{0}} \phi_{0, i_{1}, i_{0}}\left(x_{i_{0}}\right)\right)\right)\right) \cdots\right)$

1.3 KAN与MLP的异同

1.3.1 MLP如何扩深、扩宽

类似的，MLP也可以扩展到比较深、宽，比如写成仿射变换 W和非线性 σ的交错

$\operatorname{MLP}(\mathbf{x})=\left(\mathbf{W}_{L-1} \circ \sigma \circ \mathbf{W}_{L-2} \circ \sigma \circ \cdots \circ \mathbf{W}_{1} \circ \sigma \circ \mathbf{W}_{0}\right) \mathbf{x}$

很明显，MLPs将线性变换和非线性分开处理，分别表示为 W和 σ，而KANs将它们全部合
并在 Φ中。如下图(c)和(d)所示，便是一个一个三层MLP和一个三层KAN

总结一下

与MLPs类似，KANs具有全连接结构
然而，MLPs在节点——「神经元」上具有固定的激活函数，而KANs在边——「权重」上具有可学习的激活函数，如下图所示

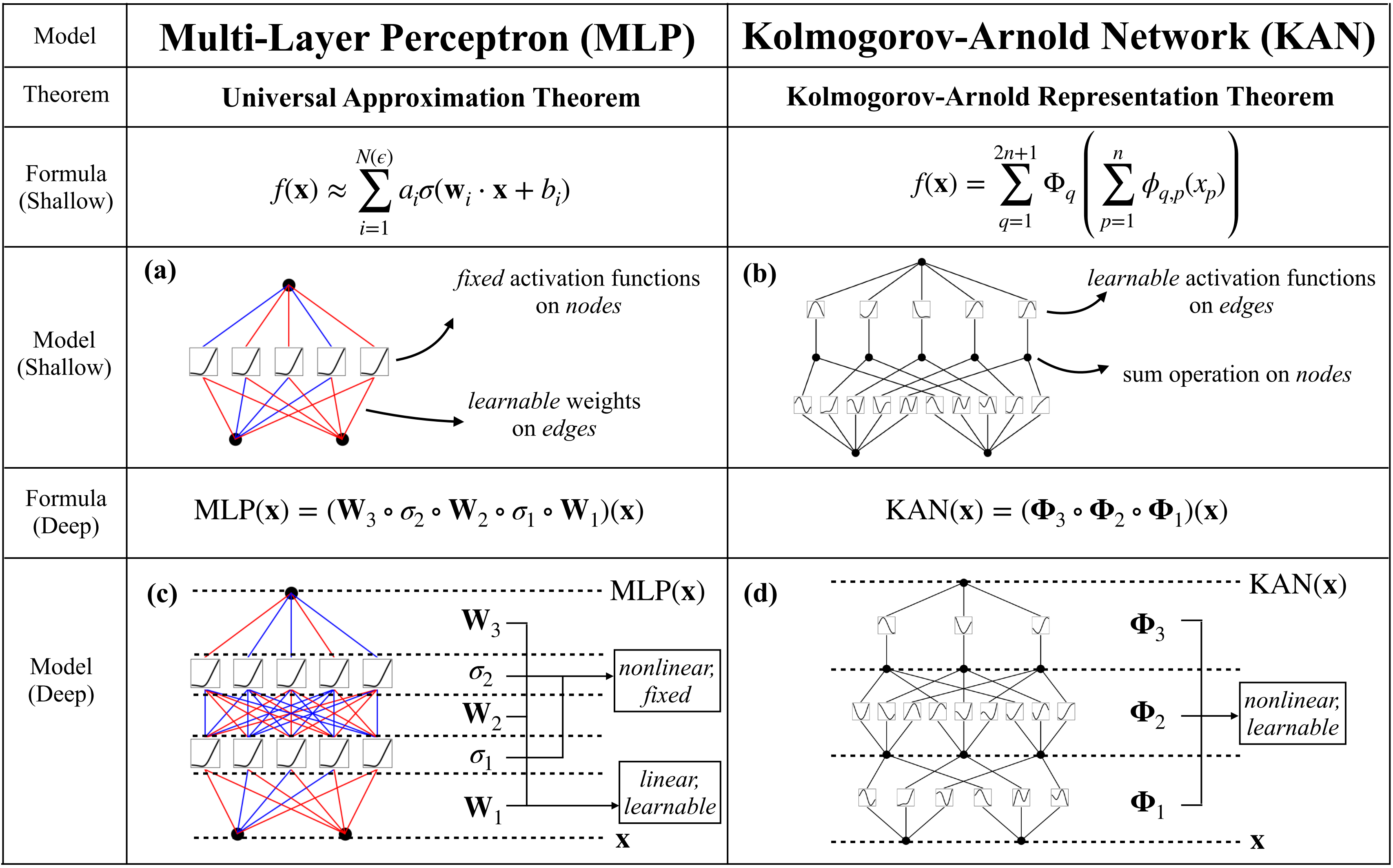
因此，KANs根本没有线性权重矩阵：相反，每个权重参数都被可学习的一维函数取代，参数化为样条函数
且KANs的节点只是简单地对传入信号求和，而不施加任何非线性

1.3.2 KANs = splines(低维函数中准确) + MLPs(可学习组合结构)

事实上，KANs只不过是splines和MLP的组合，结合了各自的优势，比如

splines在低维函数中是准确的，易于局部调整，并能够在不同分辨率之间切换。然而，splines存在严重的维度问题，无法利用组合结构(splines have a serious curse of dimensionality (COD) problem, because of their inability to exploit compositional structures)
另一方面，MLP相对于维度问题的影响较小(归功于它们的特征学习)，但在低维度下比splines不够准确，无法优化单变量函数(because of their inability to optimize univariate function)

由于KANs

在内部有splines「splines有内部自由度，但没有外部自由度，即splines有内无外，至于所谓自由度，指的是The computational graph of hown odes are connected represents external degrees of freedom (即节点之间的连接代表自由度：“dofs")」
还可以将这些学到的特征优化到极高的准确度(与样条的内部相似性)，即可以很好地近似单变量函数(即learning univariate functions)
且在外部有MLPs(MLPs有外部自由度，但没内部自由度，MLPs有外无内)
因此，KANs不仅可以学习特征(与MLPs的外部相似性)，即可以学习多个变量的组合结构(learning compositional structures of multiple variables)

例如，给定一个高维函数

$f\left(x_{1}, \cdots, x_{N}\right)=\exp \left(\frac{1}{N} \sum_{i=1}^{N} \sin ^{2}\left(x_{i}\right)\right)$

对于大 N，splines会因为COD而失败；MLPs潜在地可以学习广义可加结构，但对于用ReLU激活函数来近似指数和正弦函数非常低效。相比之下，KANs可以很好地学习组合结构和单变量函数，因此在性能上远远优于MLPs

1.3.3 KAN做的一系列优化

尽管上文的公式2.5看起来好像挺简单，但要让其work的更好还需要做一系列优化

$x_{l+1, j}=\sum_{i=1}^{n_{l}} \tilde{x}_{l, j, i}=\sum_{i=1}^{n_{l}} \phi_{l, j, i}\left(x_{l, i}\right), \quad j=1, \cdots, n_{l+1}$

残差激活函数
包括一个基函数 $b(x)$ (类似于残差连接)，使激活函数 $\phi(x)$ 为基函数 $b(x)$ 和spline函数的和
$\phi(x)=w(b(x)+\operatorname{spline}(x))$

对于前者，可设置
$b(x)=\operatorname{silu}(x)=x /\left(1+e^{-x}\right)$
对于后者，在大多数情况下， spline(x)被参数化为B-splines的线性组合，使得
$\operatorname{spline}(x)=\sum_{i} c_{i} B_{i}(x)$
其中， $c_i$ 是可训练的

最后，虽然 $w$ 可以被吸收到 $b(x)$ 和 $spline(x)$ 中。然而，KAN的作者团队仍然通过这个 $w$ 因子来更好地控制激活函数的整体幅度
初始化规模
每个激活函数的初始化值为 $\text { spline }(x) \approx 0$ (这是通过绘制 B 样条系数 ci∼ N (0, σ2)来完成的，其中σ很小，通常我们设置σ= 0.1)
$w$ 则根据Xavier初始化进行初始化(该初始化方法已用于初始化MLP中的线性层)
Update of spline grids
根据其输入激活实时更新每个格网，以解决splines在有界区域上定义，但激活值在训练过程中可能超出固定区域的问题(We update each grid on the fly according to its input activations, to address the issue that splines are defined on bounded regions but activation values can evolve out of the fixed region during training)

至于其他的可能性解决办法，包括：
(a) 使用梯度下降使格网可学习，例如[16]；(b) 使用归一化使输入范围固定

so，到底最终应该使用KANs还是MLPs？如作者团队所说

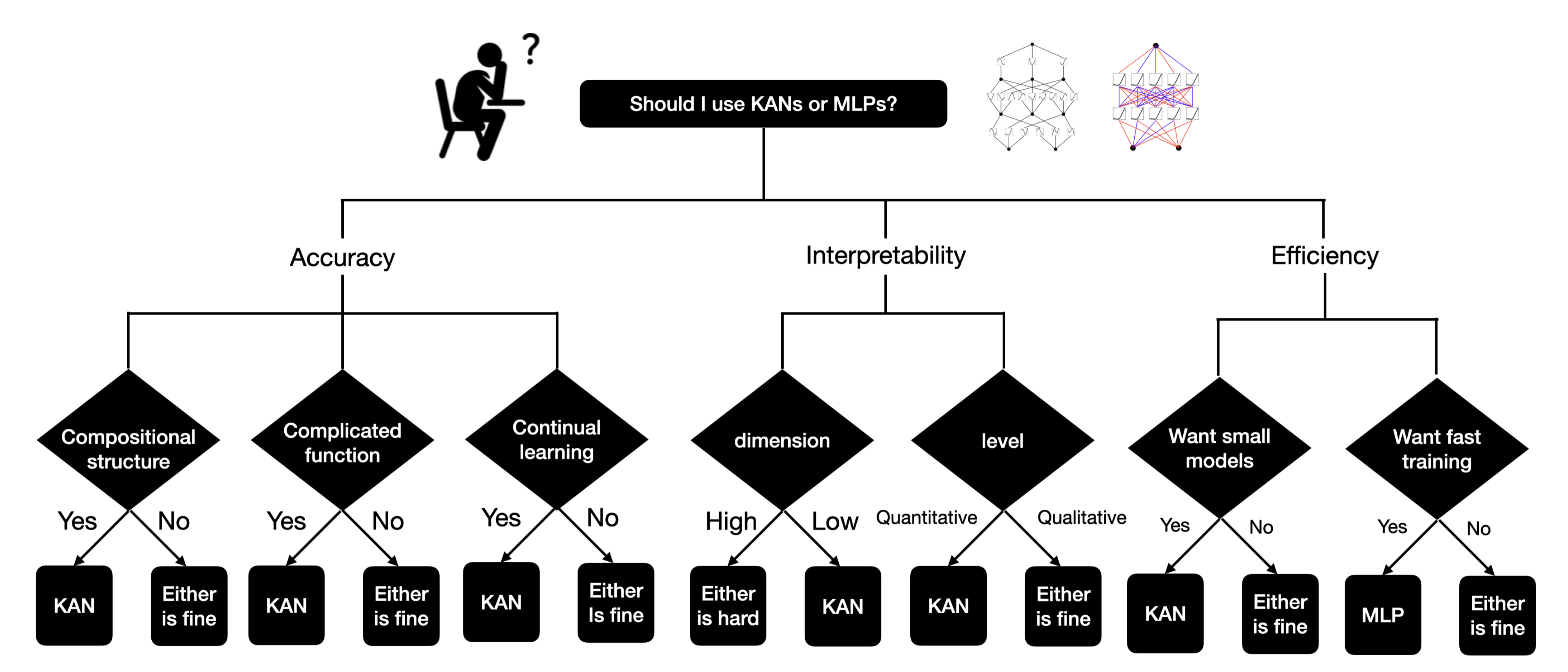
目前，KANs最大的瓶颈在于其训练速度较慢。在相同数量的参数情况下，KANs通常比MLPs慢10倍。KANs的训练速度较慢更多地是一个需要在未来改进的工程问题，而不是一个基本限制，如果一个人想要快速训练模型，应该使用MLPs
然而，在其他情况下，KANs应该与MLPs相当或更好，这使得值得尝试，简而言之，如果关心可解释性和/或准确性，并且慢速训练不是一个主要问题，可尝试使用KANs

第二部分 KAN的逼近能力、准确性、其可解释性

2.1 KAN的逼近能力

2.1.1 针对KAN逼近能力的分析：对公式2.15的解释

回想一下，在方程2.1中，层数为2且宽度为(2n+ 1)的表示基本是不平滑的，而更深层的表示可能带来更smoother activations的优势，例如，4变量函数

$f\left(x_{1}, x_{2}, x_{3}, x_{4}\right)=\exp \left(\sin \left(x_{1}^{2}+x_{2}^{2}\right)+\sin \left(x_{3}^{2}+x_{4}^{2}\right)\right)$

可以通过一个 $[4,2,1,1]$ 的KAN来平滑表示(层数是3层)，但2层KAN便可能没法具备平滑激活性

为了便于逼近分析

我们考虑允许表示成任意宽和深，以具备激活平滑性，如方程2.7 $\operatorname{KAN}(\mathbf{x})=\left(\boldsymbol{\Phi}_{L-1} \circ \boldsymbol{\Phi}_{L-2} \circ \cdots \circ \boldsymbol{\Phi}_{1} \circ \boldsymbol{\Phi}_{0}\right) \mathbf{x}$ 中所示「To facilitate an approximation analysis, we still assume smoothness of activations, but allow the representations to be arbitrarily wide and deep, as in Eq. (2.7)」
且为了强调KAN对有限网格点集的依赖性，接下来使用 $\boldsymbol{\Phi}_{l}^{G}$ 和 $\Phi_{l, i, j}^{G}$ 来替换方程2.5 $x_{l+1, j}=\sum_{i=1}^{n_{l}} \tilde{x}_{l, j, i}=\sum_{i=1}^{n_{l}} \phi_{l, j, i}\left(x_{l, i}\right), \quad j=1, \cdots, n_{l+1}$ 和2.6中使用的 $\Phi_{l}$ 和 $\Phi_{l, i, j}$

从而有以下定理

定理 2.1 逼近理论——KAT(相当于KAN在有限网格大小下逼近目标函数 $f$ 的误差界)

假设一个函数 $f(x)$ 具有表示

$f=\left(\boldsymbol{\Phi}_{L-1} \circ \boldsymbol{\Phi}_{L-2} \circ \cdots \circ \boldsymbol{\Phi}_{1} \circ \boldsymbol{\Phi}_{0}\right) \mathbf{x}$

如同方程2.7 $\operatorname{KAN}(\mathbf{x})=\left(\boldsymbol{\Phi}_{L-1} \circ \boldsymbol{\Phi}_{L-2} \circ \cdots \circ \boldsymbol{\Phi}_{1} \circ \boldsymbol{\Phi}_{0}\right) \mathbf{x}$ ，其中每一个 $\Phi_{l, i, j}$ 都是 $(k+ 1)$ 次连续可微的
那么存在一个取决于 $f$ 和其表示的常数 $C$ ，使得有以下关于网格大小 $G$ 的逼近界限：
存在k-th order B-spline函数 $\Phi_{l, i, j}^{G}$ ，对于任意 $0 \leq m \leq k$ ，有界限(such that we have the following approximation bound in terms of the grid size G: there exist k-th order B-spline functions ΦGl,i,jsuch that for any 0 ≤ m ≤ k, we have the bound，以下公式定义为2.15)
$\left\|f-\left(\boldsymbol{\Phi}_{L-1}^{G} \circ \boldsymbol{\Phi}_{L-2}^{G} \circ \cdots \circ \boldsymbol{\Phi}_{1}^{G} \circ \boldsymbol{\Phi}_{0}^{G}\right) \mathbf{x}\right\|_{C^{m}} \leq C G^{-k-1+m}$

这里作者采用 $C^{m} \text {-norm }$ 来衡量直到 m阶导数的大小
$\|g\|_{C^{m}}=\max _{|\beta| \leq m} \sup _{x \in[0,1]^{n}}\left|D^{\beta} g(x)\right|$

上面这里确实有点绕，我个人一开始看到的时候也是细想了好一会，为方便大家一目了然，我再好好解释下

其中的 $f$ 是目标函数(一个多变量函数)，我们希望用KAN来近似它
$\Phi_{l}^{(G)}$ 表示在第 $l$ 层使用的B样条函数，其中 $G$ 表示样条网格的尺寸(说白了， $G$ 就是网格的大小，表示每个B样条分段的数量)
随着 $G$ 的变大(意味着使用更大、更细的网格)，spline函数的细节和复杂性增加，从而能够更精确地逼近目标函数 $f$
$x$ 表示输入向量
$\|\cdot\|_{C^{m}}$ 表示 $C^{m}$ 范数下的误差，用于衡量函数函数及其导数的最大误差(m相当于在误差测量中考虑的导数阶数，最高到 m 阶)
不等式右边中的 $C$ 是一个依赖于目标函数 $f$ 及其表示的常数
$k$ ：B样条的阶数，通常是3(表示三次样条)
$-k-1+m$ 的项展示了B样条的逼近能力，对于光滑函数，当 m 增加时，逼近误差的收敛速度会减慢，但仍保持多项式速率
$G^{-k-1+m}$ 表示误差界随网格尺寸 $G$ 和spline的阶数 $k$ 而变化
换言之，误差的上界随着 G 的增大以 $G^{-k-1+m}$ 的速率下降

总之，这个公式2.15描述了随着样条网格细化，KANs模型近似真实函数 $f$ 的精度如何提高，即通过增加网格点的数量(G越大、网格越大越细)，可以系统地减少近似误差，从而提高模型的预测准确性(意味着需要尽可能选择合适的网格尺寸 $G$ 和spline阶数 $k$ ，以达到所需的近似精度)

2.1.2 一个说明KAN逼近能力的示例：地形图的绘制

还是为了方便更好的理解公式2.15，我再举个例子

$\left\|f-\left(\boldsymbol{\Phi}_{L-1}^{G} \circ \boldsymbol{\Phi}_{L-2}^{G} \circ \cdots \circ \boldsymbol{\Phi}_{1}^{G} \circ \boldsymbol{\Phi}_{0}^{G}\right) \mathbf{x}\right\|_{C^{m}} \leq C G^{-k-1+m}$

假设现在有一个任务是绘制一个复杂的地形图。在这个任务中，地形图是由多个不同的高度点组成的，我们希望用一种方法可以尽可能准确地预测任何位置的高度。这里的地形图就像函数 $f$ ，而我们想要用KANs来近似这个函数

样条spline网格：Grid Size $G$
想象一下，你有一个网格来帮助你绘制地形。网格越密集，你描绘地形的细节就越多，预测的高度就越精确。这个网格就像spline中的网格尺寸 $G$ ，网格的大小决定了你可以捕获的细节程度。增加 $G$ (即增加网格点的数量)，就像是用更多的点来绘制地形图，使得最终的图像更接近实际地形
函数近似误差 $\|f-\operatorname{KAN}(x)\|_{C_{m}}$
这表示用KAN模型绘制的地形图与实际地形之间的差异。理想情况下，我们希望这个差异尽可能小，这样我们的地形图就越准确
精度提高的速率 $G^{-k-1+m}$
这部分告诉我们，通过增加网格点的数量，我们可以减少地形图与实际地形之间的差异。具体来说，如果 $k$ (样条的复杂度或者阶数)、 $m$ (关注的误差的细节层次，如是否考虑地形的平滑度等)是已知的( $0 \leq m \leq k$ )，那么我们可以预测增加网格点的数量将如何提高我们模型的精确度

再比如你正在用一张低分辨率的照片来重建一个实景，低分辨率的照片可能只能捕捉到较大的特征，细节部分会模糊不清。随着照片分辨率的提高(相当于增加 $G$ )，你可以看到更多细节，从而更精确地重建实景

这就是公式 2.15 在数学上描述的现象：通过提高分辨率(增加样条网格尺寸)，你的近似(地形图或KAN模型的输出)将更接近真实(实际地形或目标函数 $f$ ）

// 待更

2.2 如何对KAN进行网格扩展(For accuracy: Grid Extension)

2.2.1 将一个新的细粒度样条拟合到一个旧的粗粒度样条上

原则上，样条可以被制作得足够精确，以逼近目标函数，因为网格可以被制作得足够细粒化。这一优点被KANs所继承

MLPs没有“细粒化”的概念
虽然增加MLPs的宽度和深度可以提高性能(比如通过““neural scaling laws”)。然而，这些神经缩放定律是缓慢的且也很昂贵，因为需要独立训练不同尺寸的模型。
对于KANs，可以先训练具有较少参数的KAN，然后通过简单地使其样条网格更细来将其扩展为具有更多参数的KAN，而无需重新从头开始训练较大的模型

接下来我们描述如何进行网格扩展(如之前下图的右侧所示，算是第二次引用上文的这个图以做说明)，基本上是将一个新的细粒度样条拟合到一个旧的粗粒度样条上

假设我们想要在有界区间 [a, b]中用阶为 k的B样条逼近一个一维函数 f

一个粗粒度的网格有 $G_1$ 个间隔，在 $\left\{t_{0}=a, t_{1}, t_{2}, \cdots, t_{G_{1}}=b\right\}$ ，可以被增强到 $\left\{t_{-k}, \cdots, t_{-1}, t_{0}, \cdots, t_{G_{1}}, t_{G_{1}+1}, \cdots, t_{G_{1}+k}\right\}$ ，即有 G1 + kB样条基函数，且第 $i$ 个B样条 $Bi(x)$ 仅在 $\left[t_{-k+i}, t_{i+1}\right]\left(i=0, \cdots, G_{1}+k-1\right)$ 上非零
然后，在粗网格上， $f$ 用这些B样条基函数的线性组合表示
$f_{\text {coarse }}(x)=\sum_{i=0}^{G_{1}+k-1} c_{i} B_{i}(x)$
给定一个细网格，有 $G_2$ 间隔，细网格上的 $f$ 相应地是
$f_{\text {fine }}(x)=\sum_{j=0}^{G_{2}+k-1} c_{j}^{\prime} B_{j}^{\prime}(x)$
其中，参数 $c_{j}^{\prime} \mathrm{s}$ 可以从参数 $c_i$ 通过最小化 $f_{\text {fine }}(x)$ 和 $f_{\text {coarse }}(x)$ 之间的距离(在某些x的分布上)来初始化(以下公式定义为2.16)：
$\left\{c_{j}^{\prime}\right\}=\underset{\left\{c_{j}^{\prime}\right\}}{\operatorname{argmin}} \underset{x \sim p(x)}{\mathbb{E}}\left(\sum_{j=0}^{G_{2}+k-1} c_{j}^{\prime} B_{j}^{\prime}(x)-\sum_{i=0}^{G_{1}+k-1} c_{i} B_{i}(x)\right)^{2}$
这可以通过最小二乘算法实现(独立地为KAN中的所有样条执行网格扩展)

2.2.2 网格扩展的示例

作者使用一个简单示例 $f(x, y)=\exp \left(\sin (\pi x)+y^{2}\right)$ 来演示网格扩展的效果

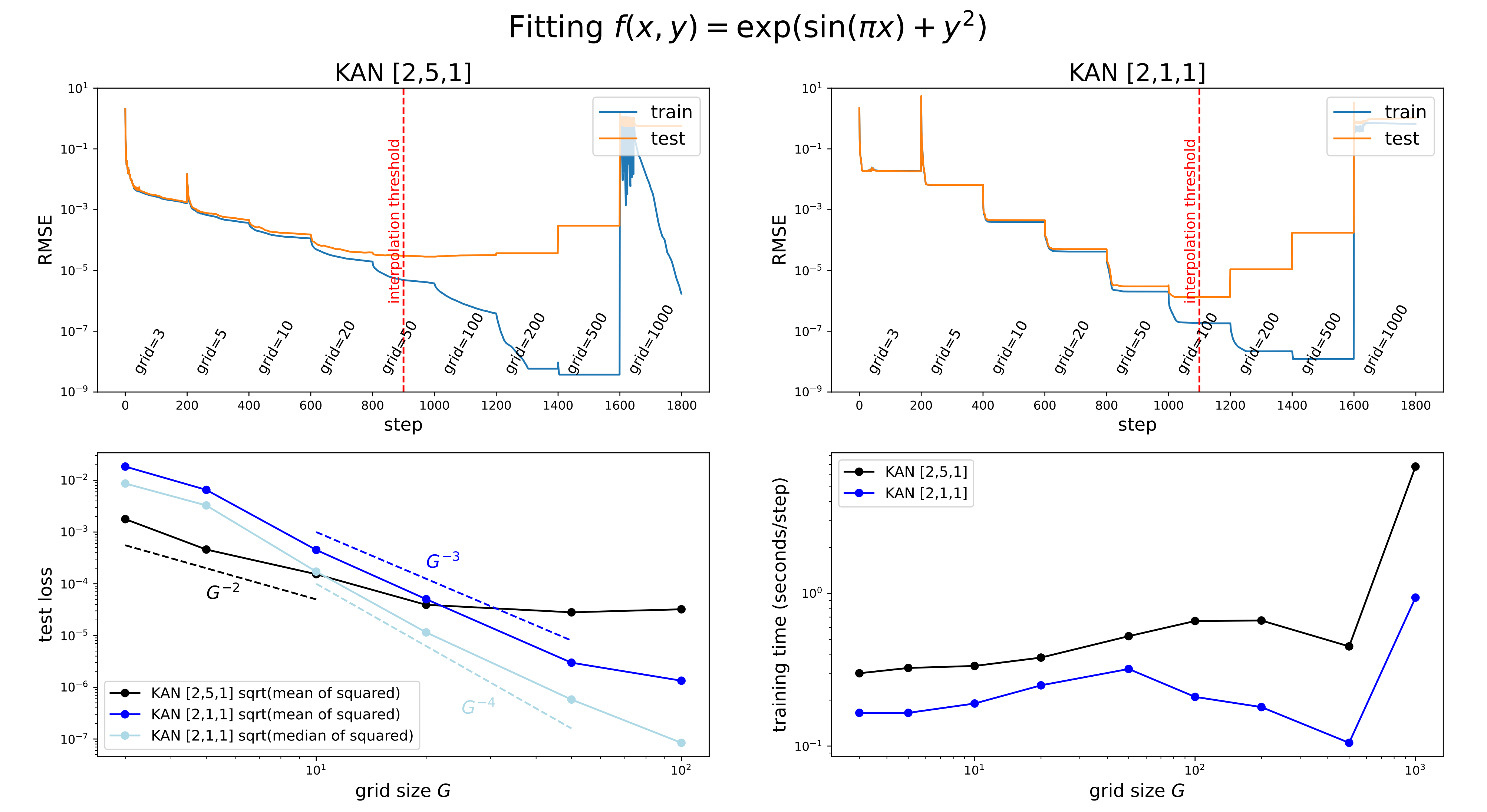
如上图左上角所示，展示了一个 [2, 5, 1]KAN的训练和测试RMSE
网格点的数量从3开始，每200个LBFGS步骤增加到更高的值，最终达到1000个网格点
很明显，每次进行精细化处理时，训练损失下降速度比以前快(除了具有1000个点的最细网格，由于糟糕的loss landscapes，优化停止工作)
然而，测试损失先下降然后上升，显示出U形状，这是由于偏差-方差权衡(欠拟合与过拟合)造成的
作者推测，当参数数量与数据点数量匹配时，最佳测试损失是在插值阈值处实现的(We conjecture that the optimal test loss is achieved at the interpolation threshold when the number of parameters match the number of data points)
比如由于训练样本有1000个，而一个[2, 5, 1]KAN的总参数为 $15$ $\times$ $G$ (G是网格间隔的数量)，作者预计插值阈值为G= 1000/15 ≈ 67，这与作者实验观察到的值 G ∼ 50大致吻合
如上图右上角所示，作者训练一个 [2, 1, 1]KAN
有趣的是，它甚至可以比 [2, 5, 1]KAN实现更低的测试损失，具有更清晰的阶梯结构，
并且由于参数更少，插值阈值延迟到更大的网格大小(在1100左右)
如上图左下角所示，随着网格数量的增加：比如从 $G^{-2}$ 、 $G^{-3}$ 到 $G^{-4}$ ，测试的损失也会随之而降低
且可以看到(为方便大家把图和文字一一对应，所以下面在描述不同的曲线时，我特意用了不同的颜色)
$\rightarrow$ 一个[2,1,1] KAN的测试RMSE大致按照测试RMSE ∝ $G^{-3}$ 的比例变化(a [2,1,1] KAN scales roughly as test RMSE ∝ G−3)
$\rightarrow$ 且当绘制平方根的中位数(而不是均值)的平方损失时，[2,1,1] KAN的测试RMSE则更接近 $G^{-4}$ 的缩放(If we plot the square root of the median (not mean) of the squared losses, we get a scaling closer to G−4. 其实这样才正常，毕竟according to the Theorem 2.1, we would expect test RMSE ∝ G−4)
最后，如上图右下角所示，训练时间随着网格点数 G的增加而有利
比如无论是[2,5,1] KAN，还是[2,1,1] KAN，在后半段(除了最后一小节)都有一段随着网格点数增加而训练时间减少的走势，特别是后者[2,1,1] KAN

2.3 KAN的可解释性：简化KANs并使其与更好用

2.3.1 简化技术：如何让KAN自动匹配某个确定函数生成的数据集

有个问题是，如果知道数据集是通过公式 $f(x, y)=\exp \left(\sin (\pi x)+y^{2}\right)$ 生成的，那么如何知道一个 [2, 1, 1]KAN能够表达这个函数呢？因此，最好有方法可以自动确定这种形状

解决办法是从一个足够大的KAN开始，然后通过稀疏正则化和修剪来训练它(这些修剪后的KAN比未修剪的更具可解释性)

稀疏化Sparsification(相当于预处理)
对于MLP，使用线性权重的L1正则化来偏好稀疏性(L1 regularization of linear weights is used to favor sparsity)
KAN可以采纳MLP这个思路，但需要两个修改：
(1) KAN中没有线性“权重”，因为线性权重被可学习的激活函数取代了，因此需要定义这些激活函数的L1范数
(2) 但L1对于KAN的稀疏化是不够的，所以还需要额外的熵正则化

综上两点，我们
$\rightarrow$ 先定义激活函数 $\phi$ 的L1范数：为其在其 $N_{p}$ 个输入上的平均幅度，即
$|\phi|_{1} \equiv \frac{1}{N_{p}} \sum_{s=1}^{N_{p}}\left|\phi\left(x^{(s)}\right)\right|$
然后对于具有 n输入和 n输出的KAN层 $\Phi$ ，定义 $\Phi$ 的L1范数为所有激活函数的L1范数之和，即
$|\boldsymbol{\Phi}|_{1} \equiv \sum_{i=1}^{n_{\text {in }}} \sum_{j=1}^{n_{\text {out }}}\left|\phi_{i, j}\right|_{1}$
$\rightarrow$ 此外，定义 $\Phi$ 的熵为
$S(\boldsymbol{\Phi}) \equiv-\sum_{i=1}^{n_{\text {in }}} \sum_{j=1}^{n_{\text {out }}} \frac{\left|\phi_{i, j}\right|_{1}}{|\boldsymbol{\Phi}|_{1}} \log \left(\frac{\left|\phi_{i, j}\right|_{1}}{|\boldsymbol{\Phi}|_{1}}\right)$
从而，总训练目标 $\ell_{\text {total }}$ 是， $\ell_{\text {pred }}$ 加上所有KAN层的L1和熵正则化：
$\ell_{\text {total }}=\ell_{\text {pred }}+\lambda\left(\mu_{1} \sum_{l=0}^{L-1}\left|\boldsymbol{\Phi}_{l}\right|_{1}+\mu_{2} \sum_{l=0}^{L-1} S\left(\boldsymbol{\Phi}_{l}\right)\right)$
其中 μ1, μ2是通常设置为 μ1 = μ2= 1的相对大小，而 λ控制整体正则化幅度
可视化Visualization
当可视化一个KAN时，为了感受到幅度，将激活函数 $\phi_{l, i, j}$ 的透明度设
置成 $\tanh \left(\beta A_{l, i, j}\right)$ 的比例，其中 β= 3。因此，具有较小幅度的函数会被忽略，好聚焦于重要函数(When we visualize a KAN, to get a sense of magnitudes, we set the transparency of an activation function ϕl,i,j proportional to tanh(βAl,i,j ) where β = 3 . Hence, functions with small magnitude appear faded out to allow us to focus on important ones)
剪枝Pruning
在使用稀疏化惩罚进行训练后，一般还需要将网络修剪到一个较小的子网络
作者在节点级别上对KAN进行稀疏化(而不是在边缘级别上)，比如对于每个节点(比如第 $i$ 个神经元在第 $l$ 层)，定义其传入和传出分数为
$I_{l, i}=\max _{k}\left(\left|\phi_{l-1, k, i}\right|_{1}\right), \quad O_{l, i}=\max _{j}\left(\left|\phi_{l+1, j, i}\right|_{1}\right)$
并且考虑一个节点是否重要，如果传入和传出分数都大于一个阈值超参数 $\theta=10^{-2}$ (默认情况下)，则这些所有不重要的神经元都被修剪
Symbolification
在我们怀疑某些激活函数实际上是符号化的情况下(例如cos或 log)，提供一个接口来将它们设置为指定的符号形式(we provide an interface to set them to be a specified symbolic f)，fix_symbolic(l,i,j,f)可以将 $(l, i, j)$ 激活设置为 $f$
然而，不能简单地将激活函数设置为精确的符号公式，因为它的输入和输出可能存在偏移和缩放
因此，从样本中获得预激活 x和后激活 y(we obtain preactivations x and postactivations y from samples)，并拟合仿射参数 $(a, b,c, d)$ 使得 $y \approx c f(a x+b)+d$ (这里的拟合可通过迭代网格搜索a, b 和线性回归来完成)

2.3.2 一个简单示例：如何更好的调教KAN

上一小节是理论，接下来举个例子，比如让我们再次考虑回归任务

$f(x, y)=\exp \left(\sin (\pi x)+y^{2}\right)$

给定数据点 $\left(x_{i}, y_{i}, f_{i}\right), i=1,2, \cdots, N_{p}$ , 我们需要找到与其匹配的KANs

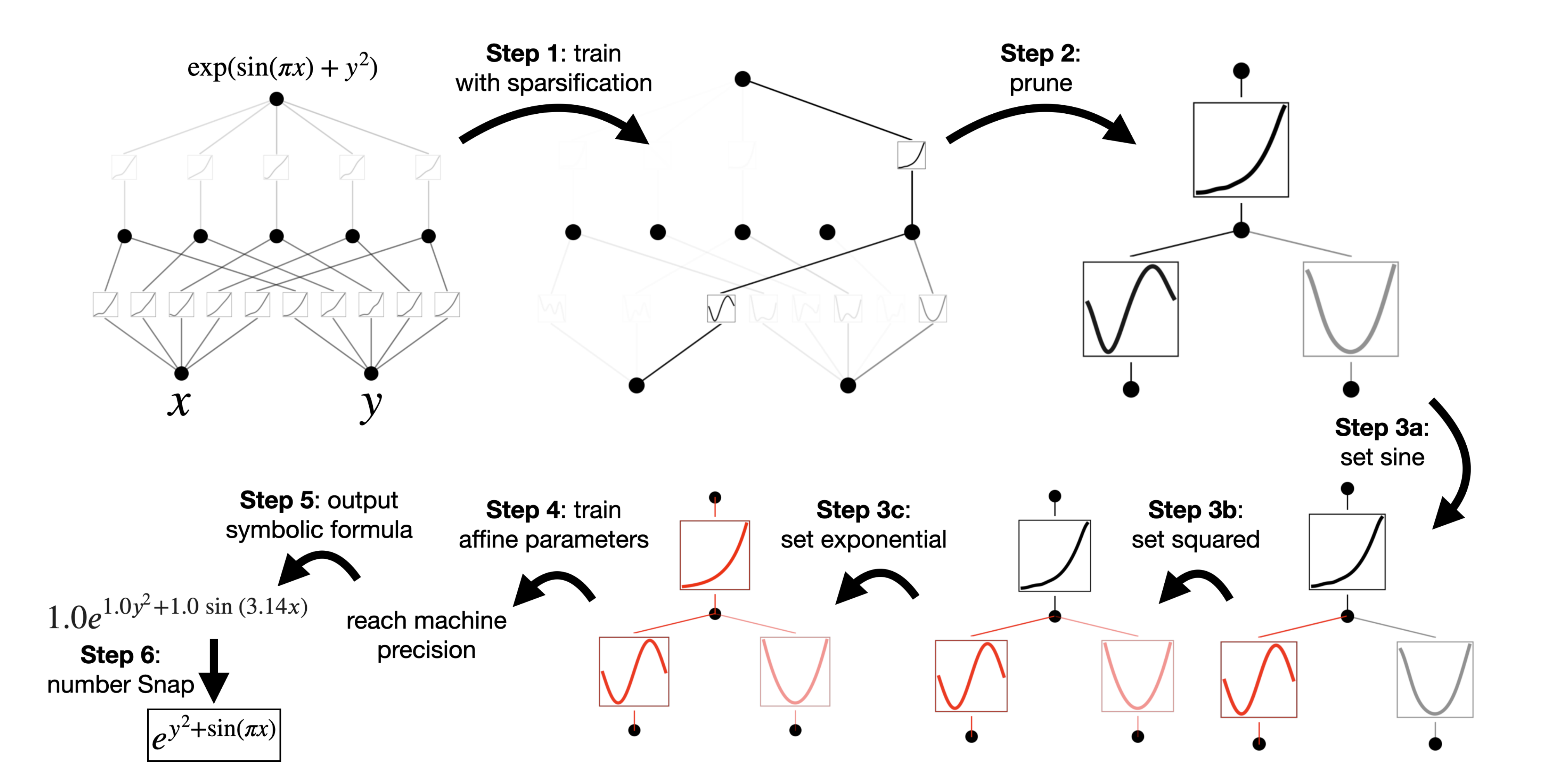
第1步：使用稀疏化进行训练
从一个全连接 [2, 5, 1]KAN开始，使用稀疏化正则化训练可以使其非常稀疏
隐藏层中的5个神经元中有4个似乎是无用的，因此我们希望将它们修剪掉
第2步：修剪
丢弃除最后一个之外的所有隐藏神经元，留下一个 [2, 1, 1]KAN，激活函数似乎是已知的符号函数
第3步：设置符号函数
假设用户可以从观察KAN图并正确猜测这些符号公式，他们可以设置为
如果用户没有领域知识或不知道这些激活函数可能是哪些符号函数，我们提供一个函数sug
gest_symbolic来建议符号候选项(we provide a function suggest_symbolic to suggest symbolic candidates)
第4步：进一步训练
在网络中将所有激活函数符号化后，唯一剩下的参数是仿射参数。我
们继续训练这些仿射参数，当我们看到损失降到机器精度时，我们知道我们已经找到了正
确的符号表达式。
第5步：输出符号公式
Sympy用于计算输出节点的符号公式。用户获得 $1.0 e^{1.0 y^{2}+1.0 \sin (3.14 x)}$ ，这是正确的答案