- 1YOLOv4 改进 | 记录如何一步一步改进YOLOv4到自己的数据集(性能、速度炸裂)
- 2获取按钮的,input框的value值_button怎样获取当前行的value
- 3Acuro二维码识别与降落对准_acuro码
- 42024年城市规划与土木建筑国际学术会议(ICUPCA 2024)
- 5sparksql执行流程_spark sql的工作流程
- 6AIGC技术简述_aigc技术包含哪些技术
- 7文心一言 v.s. ChatGPT:多角度对比测评“追赶者”能否超越?_蓝心小v和chtagpt谁更强
- 8php爬拉钩数据,node.js爬虫爬取拉勾网职位信息
- 9AI助手对决:ChatGPT vs 文心一言_ai chatgpt 文心一言
- 10毕业设计:基于机器学习的异常网络流量检测系统 信息安全_机器学习流量检测研究
数学建模 —— 层次分析法(2)_层次分析法层次总排序一致性检验
赞
踩
目录
一、层次分析法(AHP)
方法:层次分析法(Analytic Hierarchy Process)简称AHP (美国运筹学家T.L.Saaty教授在70年代中期提出)是指将决策问题的有关元素分解成目标、准则、方案等层次,在此基础上进行定性分析和定量分析的一种决策方法.
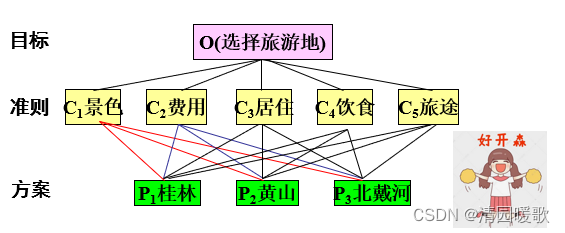
运用层次分析法建模,大体上分成四个步骤:
⑴建立递阶层次结构;
⑵构造比较判别矩阵;
⑶在单准则下的排序及一致性检验;
⑷总的排序选优。
二、构造比较判断矩阵
2.1 两两比较法
当以上一层次某个因素C作为比较准则时,可用一个比较标度aij来表达下一层次中第i个因素与第j个因素的相对重要性(或偏好优劣)的认识。aij的取值一般取正整数1—9(称为标度)及其倒数。由aij构成的矩阵称为比较判断矩阵A=(aij)。关于aij取值的规则见下表
| 元素 | 标度 | 规 则 |
| aij | 1 | 以上一层某个因素为准则,本层次因素i与因素j相比, 具有同样重要。 |
| 3 | 以上一层某个因素为准则,本层次因素i与因素j相比, i比j稍微重要。 | |
| 5 | 以上一层某个因素为准则,本层次因素i与因素j相比, i比j明显重要。 | |
| 7 | 以上一层某个因素为准则,本层次因素i与因素j相比, i比j强烈重要。 | |
| 9 | 以上一层某个因素为准则,本层次因素i与因素j相比, i比j极端重要。 |
aij取值也可以取上述各数的中值2,4,6,8及其倒数,即若因素i与因素j比较得aij,则因素j与因素i比较得1/aij。
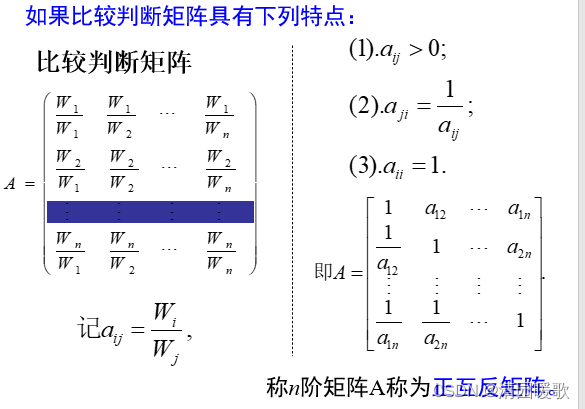
设n阶矩阵A=(aij)为正互反矩阵, 若对于一切i,j,k,都有aijajk=aik, i,j,k=1,2,…,n,称A为一致矩阵.
三、单准则下的排序及一致检验
3.1 单准则下的排序
根据比较判断矩阵如何求出各因素u1,u2,…,un , 对于准则的相对排序权重的过程称为单准则下的排序。
(1)理论依据
定理3.1.1 (Perron定理):
设n阶方阵A>O, lmax为A的模最大特征根,则
⑴ lmax必为正特征根,且对应特征向量为正向量;
⑵对于A的任何其它特征值,恒有|l|<lmax ;
⑶ lmax为A的单特征根,因而它所对应的特征向量除相差一个常数因子外是唯一的。
定理3.1.2 对于任何一个正互反矩阵均有lmax ³ n, 其中lmax为A的模最大特征根。
定理3.1.3 n阶正互反矩阵A=(aij)为一致矩阵的充分必要条件是A的最大特征根为n.
(2)求正互反矩阵排序向量的方法
①特征根方法(EVM)
对于正矩阵,有一种求特征向量的简易算法(幂法)。下面的定理为幂法提供了理论依据。

②和法

③根法

3.2 一致性检验


引入随机一致性指标RI

所以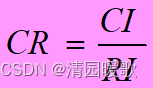
一般当CR<0.1时,认为A的不一致程度在容许范围之内,有满意的一致性,通过一致性检验。可用其归一化特征向量作为权向量,否则要重新构造成对比较矩阵A,对 aij 加以调整。
四、层次总排序
计算同一层次中所有元素对于最高层(总目标)的相对重要性标度(又称排序权重向量)称为层次总排序。
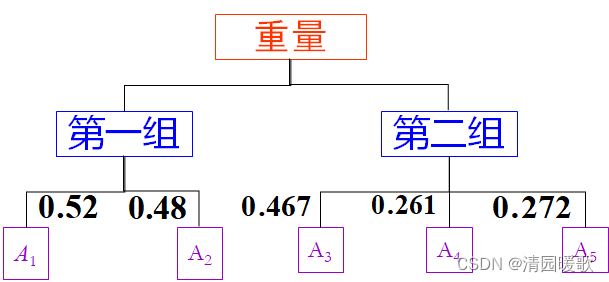
4.1 层次总排序的步骤

4.2 总排序一致性检验
人们在对各层元素作比较时,尽管每一层中所用的比较尺度基本一致,但各层之间仍可能有所差异,而这种差异将随着层次总排序的逐渐计算而累加起来,因此需要从模型的总体上来检验这种差异尺度的累积是否显著,检验的过程称为层次总排序的一致性检验。




