Dijkstra算法求最短路_叙述求解最短路的dijkstra算法基本过程

一.算法描述

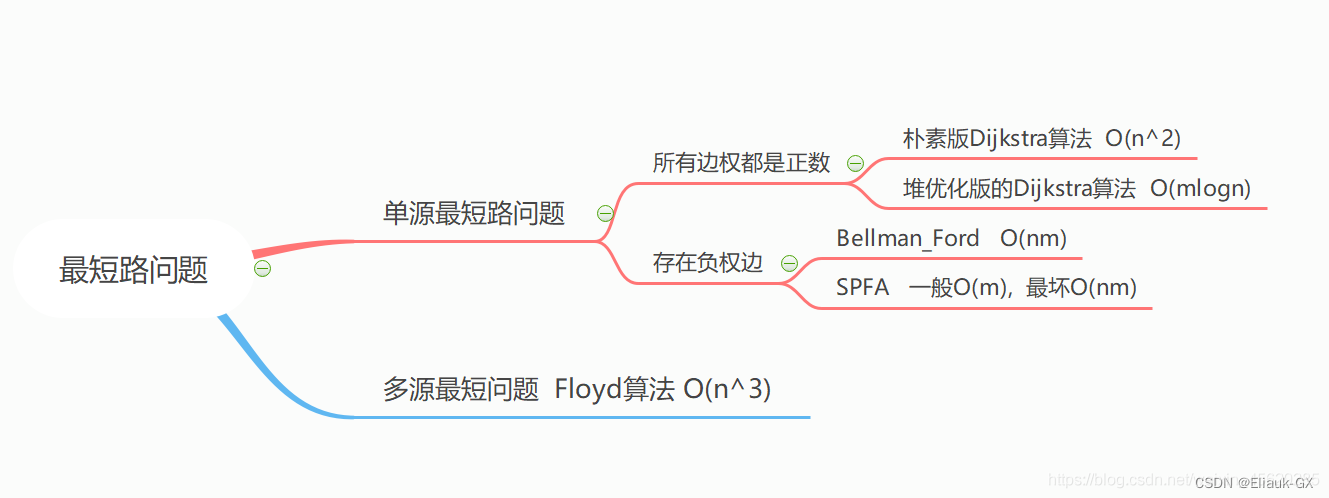
Dijkstra算法的流程如下：
1.初始化dist[1] = 0，其余节点的dist值为无穷大。
2.找出一个未被标记的、dist[x]最小的节点x，然后标记节点x。
3.扫描节点x的所有出边（x，y，z），若dist[y] > dist[x] + z，则使用dist[x] + z更新dist[y]。
4.重复上述2~3两个步骤，直到所有的节点都被标记。

Dijkstra算法基于贪心思想，它只适用于所有边的长度都是非负整数的图。当边长都是负数时，全局的最小值不可能在被其他节点更新，故在第一步中选出的节点x必然满足：dist[x]已经是起点到x的最短路径。我们不断选择全局最小值进行标记和扩展，最终得到起点1到每个节点的最短路径长度。

二.算法应用

例:对于如下有向图求1 号点到 4 号点的最短距离

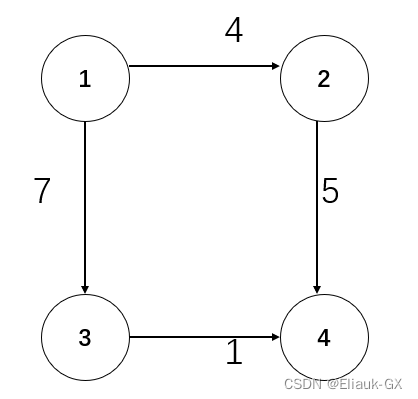
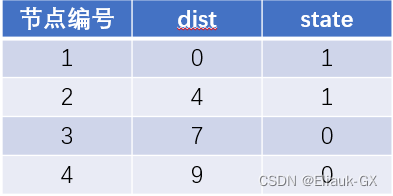
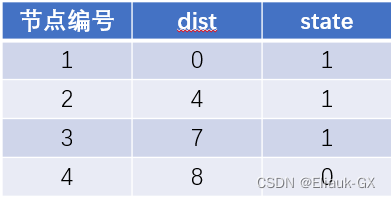
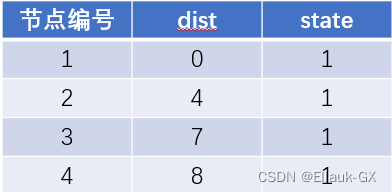
(1).初始状态原点到1号的距离为0,因此dist[1] = 0

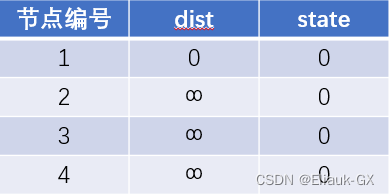
(2).遍历dist数组找到当前距离原点最近的点i并将该点进行标记,用找到的点i更新i能到的所有点的距离j,如果 dist[j] 大于 dist[i] 加上 i -> j 的距离，即 dist[j] > dist[i] + w[i][j]（w[i][j] 为 i -> j 的距离） ，则更新 dist[j] = dist[i] + w[i][j]

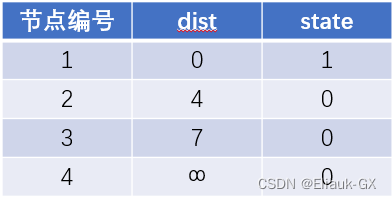
(3).重复步骤(2),直到所有的点都被标记为1

三.代码示例

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 510;
int g[N][N], dist[N];
int n, m;
bool st[N];

int dijkstra()
{
    dist[1] = 0;
    for(int i = 0; i < n; i++)
    {
        int t = -1;
        //找到未标记节点中dist最小的
        for(int j = 1; j <= n; j++)
            if(!st[j] && (t == -1 || dist[j] < dist[t]))
                t = j;
      
        st[t] = true;
        //用全局最小的值点t更新其他点
        for(int j = 1; j <= n; j++)
            dist[j] = min(dist[j], dist[t] + g[t][j]);
    }
    
    if(dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

int main()
{
    memset(dist, 0x3f, sizeof dist);
    //构建邻接矩阵
    memset(g, 0x3f, sizeof g);
    cin >> n >> m;
    for(int i = 0; i < m; i++)
    {
        int x, y, z;
        cin >> x >> y >> z;
        g[x][y] = min(g[x][y], z);
    }
    //求单源最短路径
    dijkstra();
   
    for(int i = 1; i <= n; i++) printf("%d\n", dist[i]);
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

四.算法改进

Dijkstra算法的时间复杂度为O(n^2)，主要的瓶颈在于第一步的寻找全局最小值的过程。可以用二叉堆（C++ STL priority_queue）对dist数组进行维护，用O(longn)的时间获取最小值并从堆中删除。用O(longn)的时间执行一条边的扩展和更新，最终可在O(mlongn)的时间内实现Dijkstra算法。

堆优化版的Dijkstra算法

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <vector>

#define x first
#define y second

using namespace std;

const int N = 2e5 + 10;

typedef pair<int, int> PII;

int n, m;
int h[N], e[N], ne[N], w[N], idx; //邻接表
int dist[N];
bool st[N]; //标记数组

//构建邻接表
void add(int a, int b,int c)
{
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}

int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    //pair的第一维为当前节点到原点的最短距离，第二维为节点编号
    priority_queue<PII, vector<PII>, greater<PII>> heap;
    heap.push({dist[1], 1});
    while(heap.size())
    {
        //取出堆顶
        auto k = heap.top();
        heap.pop();
        int ver = k.y, distance = k.x;
        if(st[ver]) continue;
        st[ver] = true;
        //扫描所有出边
        for(int i = h[ver]; i != -1; i = ne[i])
        {
            int j = e[i];
            if(dist[j] > distance + w[i])
            {
                //更新，把新的二元组插入堆
                dist[j] = distance + w[i];
                heap.push({dist[j], j});
            }
        }
    }
    
    if(dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}
int main()
{
    cin >> n >> m;
    memset(h, -1, sizeof h);
    //构建邻接表
    for(int i = 0; i < m; i++)
    {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }
    
    cout << dijkstra();
    return 0;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73